Задания для самостоятельного решения
Исследовать сходимость несобственных интегралов:
1.
(ответ: интеграл сходится).
2.
(ответ: интеграл сходится).
3.
(ответ: интеграл сходится).
4.
(ответ: интеграл расходится).
5.
(ответ: интеграл сходится).
6.
(ответ: интеграл расходится).
4. Интеграл как функция пределов интегрирования. Понятие о специальных функциях, определяемых интегралами с переменным верхним пределом
Определенный интеграл
можно рассматривать как функцию от а и b. Пусть a = const , а b обозначим через х. Тогда получим следующую функцию от х:
(4.1)
Дифференцируя
(4.1) по х с
учётом того, что
получаем следующее правило
дифференцирования определенного
интеграла по переменному верхнему
пределу:
(4.2)
Если верхний предел является функцией b(x), то
и вместо (4.2) будем иметь
.
Производная от элементарной функции всегда является элементарной функцией. Первообразная же от элементарной функции не всегда оказывается элементарной функцией. В связи с тем, что многие задачи математики и механики связаны с изучением и таких первообразных, возникает необходимость рассмотрения так называемых специальных функций, задаваемых при помощи интегралов с переменным пределом.
Так, в теории вероятности важную роль играет функция
(4.3)
которая называется нормальной функцией распределения.
Так как
то
функция (4.3) монотонно возрастает. В
дальнейшем мы увидим, что
Для значений функции Ф(х)
составлены таблицы.
Функция интегральный синус определяется интегралом
Особенность подынтегральной функции при t = 0 является устранимой.
Аналогично определяется интегральный логарифм
Используются и другие функции, определяемые при помощи интеграла с переменным верхним пределом.
5. Понятие об интегралах, зависящих от параметра
Рассмотрим интеграл
(5.1)
Здесь
величина х
при
интегрировании постоянна, но её значение
можно выбирать по-разному, т. е. х
является
параметром.
Очевидно, что в случае непрерывной по
t функции
формула (5.1) определяет некоторую функцию
при
Таким
образом, функцию
считаем определенной в прямоугольнике
Количество параметров может быть и большим. Например,
Интегралы, зависящие от параметров, обладают следующими свойствами:
-
если функция
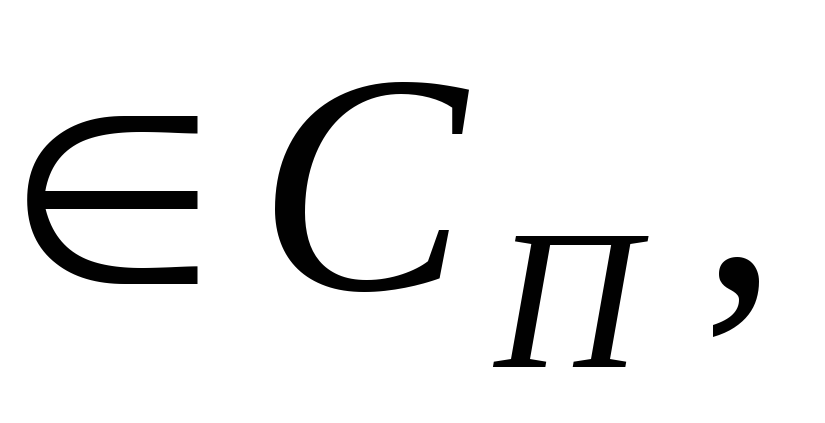то интеграл (5.1) определяет функцию
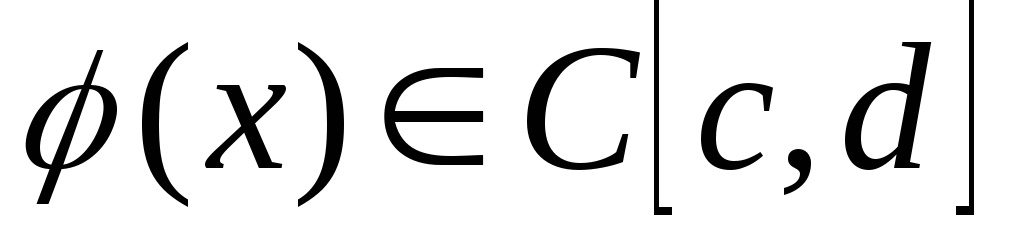и возможно интегрирование по параметру
под знаком интеграла, т. е.
;
-
если частная производная
то возможно дифференцирование по
параметру под знаком интеграла (правило
Лейбница), т. е.
.
Несобственные интегралы, зависящие от параметра, ведут себя несколько сложнее.
6. Понятие о гамма-функции
Рассмотрим интеграл, определяющий гамма-функцию (Г-функция, или эйлеров интеграл второго рода)
Этот интеграл зависит от параметра и является несобственным (с бесконечным верхним пределом). Кроме того, если х < 1, он имеет особенность при t = 0.
Установим основное свойство гамма-функции:
т. е.
(6.1)
Вычислим
Тогда,
положив в (6.1)
получим
т. е. гамма-функция является интерполирующей для факториала
(6.2)
С помощью формулы (6.2) можно определить 0!:
.
Далее, используя формулу (6.1) как определяющую, имеем
при
любых х.
Поэтому
можно продолжить
для
затем для
и т. д. В результате получается функция,
определенная всюду в R,
кроме точек х
= 0, –1, –2, …
. Чтобы окончательно выяснить поведение
Г-функции, найдем, как она изменяется
при подходе к нулю справа и слева:
,
.
Очевидно, что в целочисленных отрицательных точках Г−функция будет вести себя как в нуле (рис. 6.1).
Рис. 6.1