Задания для самостоятельного решения

1. Будет ли криволинейный интеграл

равен нулю по любому замкнутому контуру?

2. Используя формулу Грина, докажите, что площадь области D можно вычислить по одной из формул:

3. Применяя формулу Грина, вычислить интеграл , где L – контур треугольника с вершинами A(1; 1), B(2; 2), C(1; 3), пробегаемый против хода часовой стрелки (ответ: ).

4. Выяснить, зависит ли интеграл от контура интегрирования (ответ: нет).

9. Приложения кратных интегралов

9.1. Геометрические приложения кратных интегралов

I. Некоторые приложения кратных интегралов вытекают из свойств интеграла по мере области. Напомним 4-е свойство:

если f (P) 1, то , .

Конкретизируем это важное свойство:

• – длина отрезка ;

• – длина линии L;

• – площадь области D;

• – площадь поверхности Q;

• – объём тела Т.

Используя это свойство и его конкретизацию, получим формулы для вычисления таких геометрических характеристик, как объём, площадь поверхности и плоской области, длина дуги кривой.

Рассмотрим формулу для вычисления объёма тела Т

.

Пусть тело Т является правильной областью в пространстве R³, которое ограничено «снизу» поверхностью , а «сверху» − (рис. 9.1). Найдем объём тела Т:

.

Рис. 9.1

Таким образом, формула

(9.1)

применяется для вычисления объёма с помощью двойного интеграла, когда область ограничена поверхностями и и проектируется в правильную область D на плоскости х0у.

Если в формуле (9.1) положить , а , то получим формулу

, (9.2)

которая объясняет геометрический смысл двойного интеграла: двойной интеграл от функции f(x,y) по области D выражает объём цилиндрического тела, ограниченного «сверху» поверхностью , «снизу» областью D и боковой цилиндрической поверхностью, образующие которой параллельны оси 0z, а направляющая является границей области D.

Если в формуле (9.2) положить , то получим интеграл, выражающий объём цилиндра с высотой, равной 1, и основанием D. Численно этот объём равен площади основания. Итак,

. (9.3)

Очевидно, такой же результат получим, если рассмотрим третий случай свойства 4:

.

Таким образом, формула для вычисления площади плоской фигуры D имеет вид (9.3).

Произведём интегрирование в (9.3) по области D, представленной на рис. 9.2:

. (9.4)

Это выражение можно рассматривать как формулу для вычисления площади плоской фигуры D, ограниченной соответствующими линиями.

Если в (9.4) положить , а , то получим формулу для вычисления площади криволинейной трапеции, ограниченной кривой f (x), вертикальными прямыми х = а и х = b.

Замечание. При переходе к полярным, цилиндрическим и сферическим координатам получим формулы для вычисления объемов и площадей в данных координатах.

Пример 1. Вычислить площадь плоской фигуры D с помощью двойного интеграла:

1) ;

2) .

Решение

1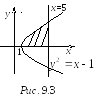. Область интегрирования ограничена прямыми , , снизу осью Ox и сверху ветвью параболы (рис. 9.3). Тогда

(кв. ед.)

2. Преобразуем уравнения области D:

.

В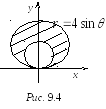 этом случае удобно воспользоваться полярными координатами, переходя к которым получим

(рис. 9.4).

Тогда

(кв. ед.)

Пример 2. Вычислить объем пространственного тела V, ограниченного поверхностями

.

Решение

Тело V сверху ограничено плоскостью , снизу − . Проекцией тела на плоскость XOY служит прямоугольник, образованный прямыми , , и (рис. 9.5). Вычислим объем фигуры, воспользовавшись формулой (9.2):

(куб. ед.).

Пример 3. Вычислить объем пространственной области V, ограниченной данными поверхностями

.

Решение

Область V ограничена тетраэдром, расположенным в первом октанте. Проекцией тела на плоскость XOY служит треугольник, образованный прямыми , , (рис. 9.6).

Следовательно,

(куб. ед.)

II. Криволинейный интеграл I рода даёт возможность получить формулы для вычисления длины дуги кривой. Их мы уже получали ранее:

– для плоской кривой, заданной уравнением ,

;

– для пространственной кривой, заданной уравнениями

;

– для плоской кривой, заданной в полярных координатах,

.

Пример 4. Найти длину первого витка винтовой линии (рис. 9.7).

Решение

III. Рассмотрим формулу 4-го случая:

− это интеграл по площади поверхности. Рассмотрим метод его вычисления.

Пусть задана поверхность Q: (рис. 9.8), dq – элемент площади поверхности, − нормальный вектор к поверхности Q в точке М.

Рис. 9.8

Если через обозначить угол между нормалью и осью , то

, где . (9.5)

За вектор можно принять вектор , где F(x, y, z) − уравнение поверхности уровня, которая в нашем случае и есть поверхность Q. Её уравнение в неявном виде

.

Итак,

.

Подставляя выражение в (9.5), получим

.

Вычислить интеграл по площади поверхности можно и с помощью двойного интеграла

.

Теперь нетрудно записать формулу для вычисления площади поверхности

.

Пример 5. Найти площадь части поверхности конуса вырезанной цилиндром (рис. 9.9).

Решение

Поверхность ограничена сверху конусом , а область D представляет собой окружность . Тогда

Так как область D есть круг радиуса a, то и площадь поверхности (кв. ед.)