
- •Часть I
- •Часть I
- •Введение
- •I. Элементы линейной алгебры
- •§1. Матрицы
- •Основные понятия
- •Действия над матрицами
- •§2. Определители
- •Основные понятия
- •2.2. Свойства определителей
- •§3. Невырожденные матрицы
- •Основные понятия
- •Обратная матрица
- •3.3. Ранг матрицы
- •§4. Системы линейных уравнений
- •Основные понятия
- •Решение систем линейных уравнений. Теорема Кронекера-Капелли
- •Решение невырожденных линейных систем. Формулы Крамера
- •Решение систем линейных уравнений методом Гаусса
- •Системы линейных однородных уравнений
- •II. Элементы векторной алгебры
- •§5. Векторы
- •5.1. Основные понятия
- •5.2. Линейные операции над векторами
- •5.3. Проекция вектора на ось
- •5.4. Разложение вектора по ортам координатных осей. Модуль вектора. Направляющие косинусы
- •5.5. Действия над векторами, заданными проекциями
- •§6. Скалярное произведение векторов и его свойства
- •6.1. Определение скалярного произведения
- •6.2. Свойства скалярного произведения
- •6.3. Выражение скалярного произведения через координаты
- •6.4. Некоторые приложения скалярного произведения
- •§ 7. Векторное произведение векторов и его свойства
- •7.1. Определение векторного произведения
- •7.2. Свойства векторного произведения
- •7.3. Выражение векторного произведения через координаты
- •7.4. Некоторые приложения векторного произведения
- •§8. Смешанное произведение векторов
- •8.1. Определение смешанного произведения, его геометрический смысл
- •8.2. Свойства смешанного произведения
- •8.3. Выражение смешанного произведения через координаты
- •8.4. Некоторые приложения смешанного произведения
- •III. Аналитическая геометрия на плоскости
- •§9. Система координат на плоскости
- •9.1. Основные понятия
- •9.2. Основные приложения метода координат на плоскости
- •9.3. Преобразование системы координат
- •§10. Линии на плоскости
- •10.1. Основные понятия
- •10.2. Уравнения прямой на плоскости
- •10.3. Прямая линия на плоскости. Основные задачи
- •§11. Линии второго порядка на плоскости
- •11.1. Основные понятия
- •11.2. Окружность
- •11.3. Эллипс
- •11.4. Гипербола
- •IV. Аналитическая геометрия в пространстве
- •§12. Уравнения поверхности и линии в пространстве
- •12.1. Основные понятия
- •12.2. Уравнения плоскости в пространстве
- •12.3. Плоскость. Основные задачи
- •12.4. Уравнения прямой в пространстве
- •12.5. Прямая линия в пространстве. Основные задачи
- •12.6. Прямая и плоскость в пространстве. Основные задачи
- •12.7. Цилиндрические поверхности
- •12.8. Поверхности вращения. Конические поверхности
- •12.9. Канонические уравнения поверхностей второго порядка
- •V. Введение в анализ
- •§13. Множества. Действительные числа
- •13.1. Основные понятия
- •13.2. Числовые множества. Множество действительных чисел
- •13.3. Числовые промежутки. Окрестность точки
- •§14. Функции
- •14.1. Понятие функции
- •14.2. Числовые функции. График функции. Способы задания функций
- •14.3. Основные характеристики функции
- •14.4. Обратная функция
- •14.5. Сложная функция
- •14.6. Основные элементарные функции и их графики
- •§15. Последовательности
- •15.1. Числовая последовательность
- •15.2. Предел числовой последовательности
- •15.3. Предельный переход в неравенствах
- •15.4. Предел монотонной ограниченной последовательности. Число . Натуральные логарифмы
- •§16. Предел функции
- •16.1. Предел функции в точке
- •16.2. Односторонние пределы
- •16.3. Предел функции при
- •16.4. Бесконечно большая функция (б.Б.Ф.)
- •§17. Бесконечно малые функции (б.М.Ф.)
- •17.1. Определения и основные теоремы
- •17.2. Связь между функцией, ее пределом и бесконечно малой функцией
- •17.3. Основные теоремы о пределах
- •17.4. Признаки существования пределов
- •17.5. Первый замечательный предел
- •17.6. Второй замечательный предел
- •§18. Эквивалентные бесконечно малые функции
- •18.1. Сравнение бесконечно малых функций
- •18.2. Эквивалентные бесконечно малые и основные теоремы о них
- •18.3. Применение эквивалентных бесконечно малых функций
- •§ 19. Непрерывность функций
- •19.1. Непрерывность функции в точке
- •19.2. Непрерывность функции в интервале и на отрезке
- •19.3. Точки разрыва функции и их классификация
- •19.4. Основные теоремы о непрерывных функциях. Непрерывность элементарных функций
- •19.5. Свойства функций, непрерывных на отрезке
- •Заключение
- •Библиографический список
- •Часть I
- •394026 Воронеж, Московский просп., 14
V. Введение в анализ
§13. Множества. Действительные числа
13.1. Основные понятия
Понятие множества является одним из основных неопределяемых понятий математики.
Определение. Под множеством понимают совокупность (собрание, класс, семейство...) некоторых объектов, объединенных по какому-либо признаку.
Так
можно говорить о множестве студентов
института, о множестве рыб в Черном
море, о множестве корней уравнения
![]() ,
о множестве всех натуральных чисел и
т. д.
,
о множестве всех натуральных чисел и
т. д.
Объекты,
из которых состоит множество, называются
его элементами.
Множества
принято обозначать заглавными буквами
латинского алфавита
![]() а их элементы — малыми буквами
а их элементы — малыми буквами
![]()
Если
элемент
принадлежит множеству
,
то записывают
![]() ;
запись
;
запись
![]() или
или
![]() означает, что элемент
не принадлежит множеству
.
означает, что элемент
не принадлежит множеству
.
Множество,
не содержащее ни одного элемента,
называется пустым,
обозначается
символом
![]() .
.
Элементы множества записывают в фигурных скобках, внутри которых они перечислены (если это возможно), либо указано общее свойство, которым обладают все элементы данного множества.
Например,
запись
= {1, 3, 15} означает, что множество
состоит из трех чисел 1, 3 и 15; запись
= {
:
![]() }
означает, что множество
состоит из всех действительных (если
не оговорено иное) чисел, удовлетворяющих
неравенству
.
}
означает, что множество
состоит из всех действительных (если
не оговорено иное) чисел, удовлетворяющих
неравенству
.
Определение.
Множество
называется подмножеством
множества
,
если каждый элемент множества
является элементом множества
.
Символически это обозначают так
![]() («
включено в
»)
или
(«
включено в
»)
или
![]() («множество
включает в себя множество
»).
(«множество
включает в себя множество
»).
Определение.
Говорят, что множества
и
равны
или
совпадают,
и пишут
![]() ,
если
и
,
если
и
![]() .
Другими
словами, множества, состоящие из одних
и тех же элементов, называются равными.
.
Другими
словами, множества, состоящие из одних
и тех же элементов, называются равными.
Определение.
Объединением
(или суммой)
множеств
и
называется множество, состоящее из
элементов, каждый из которых принадлежит
хотя бы одному из этих множеств.
Объединение (сумму) множеств обозначают
![]() (или
(или
![]() ).
Кратко Можно
записать
= {
:
).
Кратко Можно
записать
= {
:
![]() или
или
![]() }.
}.
Определение.
Пересечением
(или
произведением)
множеств
и
называется множество, состоящее из
элементов, каждый из которых принадлежит
множеству
и множеству
.
Пересечение (произведение) множеств
обозначают
![]() (или
(или
![]() ).
Кратко можно
записать
= {
:
и
).
Кратко можно
записать
= {
:
и
![]() }.
}.
В дальнейшем для сокращения записей будем использовать некоторые простейшие логические символы:
![]() — означает
«из предложения
следует
предложение
»;
— означает
«из предложения
следует
предложение
»;
![]() — «предложения
и
равносильны», т.е. из
следует
и из
следует
;
— «предложения
и
равносильны», т.е. из
следует
и из
следует
;
![]() — означает
«для любого», «для всякого»;
— означает
«для любого», «для всякого»;
![]() — «существует»,
«найдется»;
— «существует»,
«найдется»;
: — «имеет место», «такое что»;
![]() — «соответствие».
— «соответствие».
Пример
13.1. 1)
запись
![]() :
означает: «для всякого элемента
:
означает: «для всякого элемента
![]() имеет место предложение
»;
имеет место предложение
»;
2)
(![]() )
(
или
)
(
или
![]() );
эта запись
определяет
);
эта запись
определяет
объединение множеств и .
13.2. Числовые множества. Множество действительных чисел
Определение. Множества, элементами которых являются числа, называются числовыми.
Примерами числовых множеств являются:
![]() =
{1; 2; 3; …;
;
…} — множество натуральных чисел;
=
{1; 2; 3; …;
;
…} — множество натуральных чисел;
![]() =
{0; 1; 2; …;
;
…} — множество целых неотрицательных
чисел;
=
{0; 1; 2; …;
;
…} — множество целых неотрицательных
чисел;
![]() =
{0; ±1; ±2; …; ±
;
…} —
множество целых чисел;
=
{0; ±1; ±2; …; ±
;
…} —
множество целых чисел;
![]() =
=
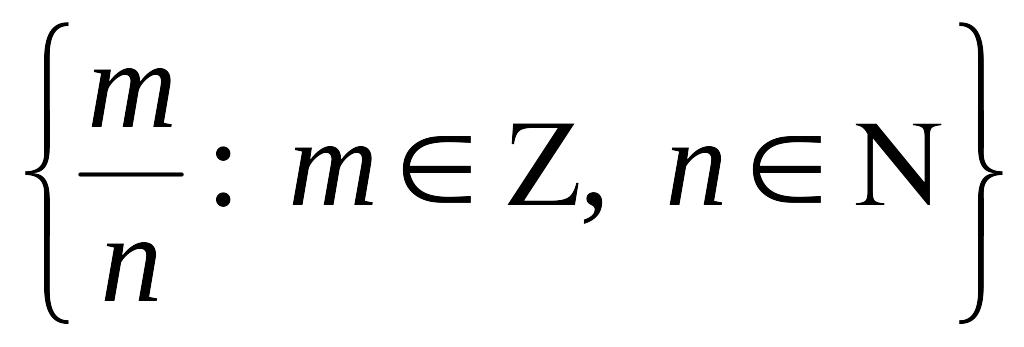 — множество рациональных чисел.
— множество рациональных чисел.
![]() — множество
действительных чисел.
— множество
действительных чисел.
Между этими множествами существует соотношение
![]() .
.
Множество
содержит рациональные и иррациональные
числа. Всякое рациональное число
выражается или конечной десятичной
дробью или бесконечной периодической
дробью. Так,
![]() = 0,5 (= 0,500…),
= 0,5 (= 0,500…),
![]() = 0,333… — рациональные числа.
= 0,333… — рациональные числа.
Определение. Действительные числа, не являющиеся рациональными, называются иррациональными.
Теорема 13.1. Не существует рационального числа, квадрат которого равен числу 2.
Доказательство.
Допустим, что существует рациональное
число, представленное несократимой
дробью
![]() ,
квадрат которого равен 2. Тогда имеем:
,
квадрат которого равен 2. Тогда имеем:
 ,
т.е.
,
т.е.
![]() (единственная) точка числовой оси и,
наоборот, каждой точке оси соответствует
определенное число. Отсюда следует, что
(единственная) точка числовой оси и,
наоборот, каждой точке оси соответствует
определенное число. Отсюда следует, что
![]() (а значит, и
(а значит, и
![]() )
— четное число, т.е.
)
— четное число, т.е.
![]() .
Подставив
в равенство
,
получим
.
Подставив
в равенство
,
получим
![]() ,
т.е.
,
т.е.
![]() .
Отсюда
следует, что число
— четное, т.е.
.
Отсюда
следует, что число
— четное, т.е.
![]() .
Но тогда
дробь
.
Но тогда
дробь
![]() сократима. Это противоречит допущению,
что
дробь несократима. Следовательно, не
существует рационального числа, квадрат
которого равен числу 2.
сократима. Это противоречит допущению,
что
дробь несократима. Следовательно, не
существует рационального числа, квадрат
которого равен числу 2.
Иррациональное
число выражается бесконечной
непериодической дробью. Так,
=
1,4142356…,
![]() =
3,1415926… — иррациональные числа. Можно
сказать: множество действительных чисел
есть множество всех бесконечных
десятичных дробей. И записать
=
3,1415926… — иррациональные числа. Можно
сказать: множество действительных чисел
есть множество всех бесконечных
десятичных дробей. И записать
=
{
:
![]() },
где
},
где
![]() ,
,
![]() {0, 1, …,9}.
{0, 1, …,9}.
Множество действительных чисел обладает следующими свойствами.
Свойство
1. Оно
упорядоченное:
для любых
двух различных чисел
и
имеет место одно из двух соотношений
![]() либо
либо
![]() .
.
Свойство
2. Множество
плотное:
между
любыми двумя различными числами
и
содержится бесконечное множество
действительных чисел
,
т.е. чисел, удовлетворяющих неравенству
![]() .
.
Так,
если
,
то одним из них является число
![]()
 .
.
Свойство
3. Множество
непрерывное.
Пусть
множество
разбито на два непустых класса
и
таких, что каждое действительное число
содержится только в одном классе и
для каждой пары чисел
![]() и
и
![]() выполнено неравенство
.
Тогда (свойство непрерывности) существует
единственное число
,
удовлетворяющее неравенству
выполнено неравенство
.
Тогда (свойство непрерывности) существует
единственное число
,
удовлетворяющее неравенству
![]() (
(![]() ,
,
![]() ).
Оно отделяет
числа класса
от чисел класса
.
Число с является либо наибольшим
числом в классе
(тогда в классе
нет наименьшего числа), либо наименьшим
числом в классе
(тогда в классе
нет наибольшего).
).
Оно отделяет
числа класса
от чисел класса
.
Число с является либо наибольшим
числом в классе
(тогда в классе
нет наименьшего числа), либо наименьшим
числом в классе
(тогда в классе
нет наибольшего).
Свойство
непрерывности позволяет установить
взаимно-однозначное соответствие
между множеством всех действительных
чисел и множеством всех точек прямой.
Это означает, что каждому числу
![]() соответствует определенная (единственное)
действительное число. Поэтому вместо
слова «число» часто говорят «точка».
соответствует определенная (единственное)
действительное число. Поэтому вместо
слова «число» часто говорят «точка».
