11.3. Эллипс

Каноническое уравнение эллипса.

Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой плос­кости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.

Обозначим фокусы через и , расстояние между ними через , а сумму расстояний от произвольной точки эллипса до фокусов — через (см. рис. 49). По определению , т. е. .

Для вывода уравнения эллипса выберем систему координат так, чтобы фокусы и лежали на оси , а начало координат совпа­дало с серединой отрезка . Тогда фокусы будут иметь следующие координаты: и .

Рис. 11.2

Пусть — произвольная точка эллипса. Тогда, согласно определению эллипса, , т. е.

.

Это, по сути, и есть уравнение эллипса.

Преобразуем уравнение (11.5) к более простому виду следующим образом:

,

,

,

,

.

Так как , то . Положим

. (11.6)

Тогда последнее уравнение примет вид или

(11.7)

Можно доказать, что уравнение (11.7) равносильно исходному уравнению. Оно называется каноническим уравнением эллипса. Эллипс — кривая второго порядка.

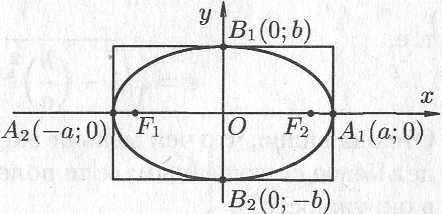
Рис. 11.3

Исследование формы эллипса по его уравнению.

Установим форму эллипса, пользуясь его каноническим уравне­нием.

1. Уравнение (11.7) содержит и только в четных степенях, по­этому если точка принадлежит эллипсу, то ему также принадле­жат точки , , . Отсюда следует, что эллипс сим­метричен относительно осей и , а также относительно точ­ки , которую называют цен­тром эллипса.

2. Найдём точки пересечения эллипса с осями координат. По­ложив , находим две точки и , в которых ось пересекает эллипс (см. рис. 11.3). Положив в уравнении (11.7) , находим точки пересечения эллипса с осью : и . Точки , , , называются вершинами эллипса. Отрезки и , а также их длины и называются соответственно большой и малой осями эллипса. Числа и называются соответственно большой и малой полуосями эллипса.

3. Из уравнения (11.7) следует, что каждое слагаемое в левой части не превосходит единицы, т.е. имеют место неравенства

и

или и .

Следовательно, все точки эллипса лежат внутри прямоугольника, образованного прямыми , .

4. В уравнении (11.7) сумма неотрицательных слагаемых

и

равна единице. Следовательно, при возрастании одного слагаемого дру­гое будет уменьшаться, т. е. если возрастает, то уменьшается и наоборот.

Из сказанного следует, что эллипс имеет форму, изображенную на рис. 11.3 (овальная замкнутая кривая).

Дополнительные сведения об эллипсе.

Форма эллипса зависит от отношения . При эллипс превра­щается в окружность, уравнение эллипса (11.7) принимает вид . В качестве характеристики формы эллипса чаще пользуются от­ношением .

Отношение половины расстояния между фокусами к большой полуоси эллипса называется эксцентриситетом эллипса и обозначается буквой («эпсилон»):

(11.8)

причем , так как . С учетом равенства (11.6) формулу (11.8) можно переписать в виде

,

т.е.

и .

Отсюда видно, что чем меньше эксцентриситет эллипса, тем эллипс бу­дет менее сплющенным; если положить , то эллипс превращается в окружность.

Рис. 11.4

Пусть — произвольная точка эллипса с фокусами и (см. рис. 11.4). Длины отрезков и называются фокальными радиусами точки . Очевидно, .

Рис. 11.5

Имеют место формулы

и .

Прямые называются директрисами эллипса. Значение директрисы эллипса выявляется следующим утверждением.

Теорема 11.1. Если — расстояние от произвольной точки эллипса до какого-нибудь фокуса, — расстояние от этой же точки до соответ­ствующей этому фокусу директрисы, то отношение есть постоянная

величина, равная эксцентриситету эллипса: .

Из равенства (11.6) следует, что . Если же , то уравне­ние (11.7) определяет эллипс, большая ось которого лежит на оси , а малая ось — на оси (см. рис. 11.5). Фокусы такого эллипса находятся в точках и , где .

Рис. 11.6