12.3. Плоскость. Основные задачи

Угол между двумя плоскостями. Условия параллельности и перпендикулярности двух плоскостей.

Пусть заданы две плоскости и :

,

.

Под углом между плоскостями и понимается один из двугранных углов, образованных этими плоскостями.

Угол между нормальными векторами и плоскостей и равен одному из этих углов (см. рис. 12.7). Поэтому

или

.

Для нахождения острого угла следует взять модуль правой части.

Если плоскости и перпендикулярны (см. рис. 12.8, а), то таковы же их нормали, т. е. (и наоборот). Но тогда ,

т.е.

.

Полученное равенство есть условие пер­пендикулярности двух плоскостей и .

Если плоскости и параллельны (см. рис. 12.8, б), то будут параллельны и их нормали и (и наоборот). Но тогда, как известно, координаты векторов пропорциональны: . Это и есть условие параллельности двух плоскостей и .

Рис. 12.7

Рис. 12.8, а Рис. 12.8, б

Расстояние от точки до плоскости.

Пусть задана точка и плоскость своим уравнением . Расстояние от точки до плоскости находится по формуле

.

Вывод этой формулы такой же, как вывод формулы расстояния от точки до прямой (см. с. 73).

Расстояние от точки до плоскости равно модулю проек­ции вектора , где — произвольная точка плоскости , на направление нормального вектора (см. рис. 61). Следовательно,

А так как точка принадлежит плоскости , то

, т.е. .

Поэтому

.

Отметим, что если плоскость задана уравнением , то расстояние отточки до плоскости может быть найдено по формуле

.

12.4. Уравнения прямой в пространстве

Векторное уравнение прямой.

Положение прямой в пространстве вполне определено, если задать какую-либо точку на прямой и вектор , параллельный этой прямой. Вектор называется направляющим вектором прямой.

Пусть прямая задана ее точкой и направляющим векто­ром . Возьмем на прямой произвольную точку . Обозначим радиус-векторы точек и соответственно через и . Очевидно, что три вектора , и связаны соотношением

. (12.10)

Рис. 12.9

Вектор , лежащий на прямой , параллелен направляюще­му вектору , поэтому , где скалярный множитель, называемый параметром, может принимать различные значения в за­висимости от положения точки на прямой (см. рис. 12.9).

Уравнение (12.10) можно записать в виде

(12.11)

Полученное уравнение называется векторным уравнением прямой.

Параметрические уравнения прямой.

Рис. 12.10

Замечая, что , , , уравне­ние (12.11) можно записать в виде

.

Отсюда следуют равенства:

(12.12)

Они называются параметрическими уравнениями прямой в простран­стве.

Канонические уравнения прямой.

Пусть — направляющий вектор прямой и — точка, лежащая на этой прямой. Вектор , соединяющий точку с произвольной точкой прямой , параллелен вектору . Поэтому координаты вектора и вектора пропорциональны:

.

Уравнения (12.13) называются каноническими уравнениями прямой в пространстве.

Замечание 1. Уравнения (12.13) можно было бы получить сразу из параметрических уравнений прямой (12.12), исключив параметр . Из уравнений (12.12) находим

.

Замечание 2. Обращение в нуль одного из знаменателей уравнений (12.13) означает обращение в нуль соответствующего числителя.

Например, уравнения

задают прямую, проходящую через точку перпендикулярно оси (проекция вектора на ось равна нулю). Но это означает, что прямая лежит в плоскости , и поэтому для всех точек прямой будет .

Уравнение прямой в пространстве, проходящей через две точки.

Пусть прямая проходит через точки и . В качестве направляющего вектора можно взять вектор , т.е. (см. рис. 12.11).

Рис. 12.11

Следовательно, , , . Поскольку прямая проходит через точку , то, согласно уравнениям (12.13), уравнения прямой имеют вид

.

Уравнения (12.14) называются уравнениями прямой, проходящей через две данные точки.

Общие уравнения прямой.

Прямую в пространстве можно задать как линию пересечения двух непараллельных плоскостей. Рассмотрим систему уравнений

.

Каждое из уравнений этой системы определяет плоскость. Если плоскости не параллельны (координаты векторов и не пропорциональны), то система (12.15) определяет прямую как геометрическое место точек пространства, координаты которых удовлетворяют каждому из уравнений системы (см. рис. 12.12). Уравнения (12.5) называют общими уравнениями прямой.

От общих уравнений (12.15) можно перейти к каноническим уравнениям (12.13). Координаты точки на прямой получаем из системы уравнений (12.15), придав одной из координат произвольное значение (например, z = 0).

Так как прямая перпендикулярна векторам и , то за направляющий вектор прямой можно принять векторное произведение :

.

Замечание. Канонические уравнения прямой легко получить, взяв две какие-либо точки на ней и применив уравнения (12.14).

Рис. 12.12

Пример 12.1. Написать канонические уравнения прямой , заданной уравнениями

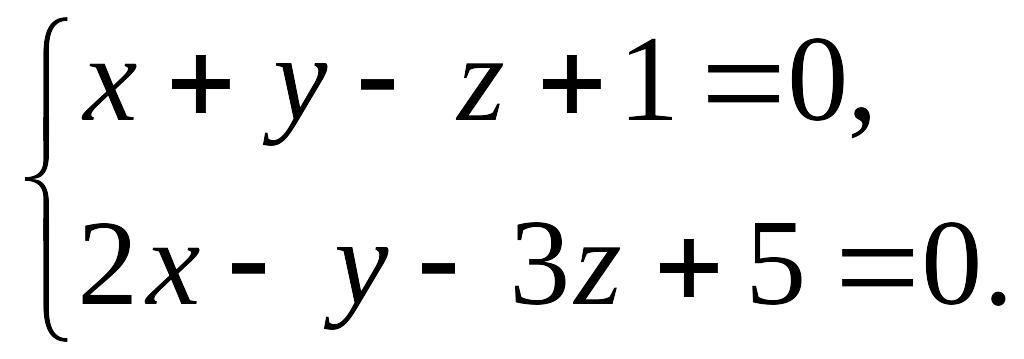
Решение. Положим и решим систему Находим точку . Положим и решим систему Находим вторую точку прямой . Записываем уравнение прямой , проходящей через точки и :

.