
- •Preface
- •Contents
- •1 Introduction
- •1.1 Physics
- •1.2 Mechanics
- •1.3 Integrating Numerical Methods
- •1.4 Problems and Exercises
- •1.5 How to Learn Physics
- •1.5.1 Advice for How to Succeed
- •1.6 How to Use This Book
- •2 Getting Started with Programming
- •2.1 A Python Calculator
- •2.2 Scripts and Functions
- •2.3 Plotting Data-Sets
- •2.4 Plotting a Function
- •2.5 Random Numbers
- •2.6 Conditions
- •2.7 Reading Real Data
- •2.7.1 Example: Plot of Function and Derivative
- •3 Units and Measurement
- •3.1 Standardized Units
- •3.2 Changing Units
- •3.4 Numerical Representation
- •4 Motion in One Dimension
- •4.1 Description of Motion
- •4.1.1 Example: Motion of a Falling Tennis Ball
- •4.2 Calculation of Motion
- •4.2.1 Example: Modeling the Motion of a Falling Tennis Ball
- •5 Forces in One Dimension
- •5.1 What Is a Force?
- •5.2 Identifying Forces
- •5.3.1 Example: Acceleration and Forces on a Lunar Lander
- •5.4 Force Models
- •5.5 Force Model: Gravitational Force
- •5.6 Force Model: Viscous Force
- •5.6.1 Example: Falling Raindrops
- •5.7 Force Model: Spring Force
- •5.7.1 Example: Motion of a Hanging Block
- •5.9.1 Example: Weight in an Elevator
- •6 Motion in Two and Three Dimensions
- •6.1 Vectors
- •6.2 Description of Motion
- •6.2.1 Example: Mars Express
- •6.3 Calculation of Motion
- •6.3.1 Example: Feather in the Wind
- •6.4 Frames of Reference
- •6.4.1 Example: Motion of a Boat on a Flowing River
- •7 Forces in Two and Three Dimensions
- •7.1 Identifying Forces
- •7.3.1 Example: Motion of a Ball with Gravity
- •7.4.1 Example: Path Through a Tornado
- •7.5.1 Example: Motion of a Bouncing Ball with Air Resistance
- •7.6.1 Example: Comet Trajectory
- •8 Constrained Motion
- •8.1 Linear Motion
- •8.2 Curved Motion
- •8.2.1 Example: Acceleration of a Matchbox Car
- •8.2.2 Example: Acceleration of a Rotating Rod
- •8.2.3 Example: Normal Acceleration in Circular Motion
- •9 Forces and Constrained Motion
- •9.1 Linear Constraints
- •9.1.1 Example: A Bead in the Wind
- •9.2.1 Example: Static Friction Forces
- •9.2.2 Example: Dynamic Friction of a Block Sliding up a Hill
- •9.2.3 Example: Oscillations During an Earthquake
- •9.3 Circular Motion
- •9.3.1 Example: A Car Driving Through a Curve
- •9.3.2 Example: Pendulum with Air Resistance
- •10 Work
- •10.1 Integration Methods
- •10.2 Work-Energy Theorem
- •10.3 Work Done by One-Dimensional Force Models
- •10.3.1 Example: Jumping from the Roof
- •10.3.2 Example: Stopping in a Cushion
- •10.4.1 Example: Work of Gravity
- •10.4.2 Example: Roller-Coaster Motion
- •10.4.3 Example: Work on a Block Sliding Down a Plane
- •10.5 Power
- •10.5.1 Example: Power Exerted When Climbing the Stairs
- •10.5.2 Example: Power of Small Bacterium
- •11 Energy
- •11.1 Motivating Examples
- •11.2 Potential Energy in One Dimension
- •11.2.1 Example: Falling Faster
- •11.2.2 Example: Roller-Coaster Motion
- •11.2.3 Example: Pendulum
- •11.2.4 Example: Spring Cannon
- •11.3 Energy Diagrams
- •11.3.1 Example: Energy Diagram for the Vertical Bow-Shot
- •11.3.2 Example: Atomic Motion Along a Surface
- •11.4 The Energy Principle
- •11.4.1 Example: Lift and Release
- •11.4.2 Example: Sliding Block
- •11.5 Potential Energy in Three Dimensions
- •11.5.1 Example: Constant Gravity in Three Dimensions
- •11.5.2 Example: Gravity in Three Dimensions
- •11.5.3 Example: Non-conservative Force Field
- •11.6 Energy Conservation as a Test of Numerical Solutions
- •12 Momentum, Impulse, and Collisions
- •12.2 Translational Momentum
- •12.3 Impulse and Change in Momentum
- •12.3.1 Example: Ball Colliding with Wall
- •12.3.2 Example: Hitting a Tennis Ball
- •12.4 Isolated Systems and Conservation of Momentum
- •12.5 Collisions
- •12.5.1 Example: Ballistic Pendulum
- •12.5.2 Example: Super-Ball
- •12.6 Modeling and Visualization of Collisions
- •12.7 Rocket Equation
- •12.7.1 Example: Adding Mass to a Railway Car
- •12.7.2 Example: Rocket with Diminishing Mass
- •13 Multiparticle Systems
- •13.1 Motion of a Multiparticle System
- •13.2 The Center of Mass
- •13.2.1 Example: Points on a Line
- •13.2.2 Example: Center of Mass of Object with Hole
- •13.2.3 Example: Center of Mass by Integration
- •13.2.4 Example: Center of Mass from Image Analysis
- •13.3.1 Example: Ballistic Motion with an Explosion
- •13.4 Motion in the Center of Mass System
- •13.5 Energy Partitioning
- •13.5.1 Example: Bouncing Dumbbell
- •13.6 Energy Principle for Multi-particle Systems
- •14 Rotational Motion
- •14.2 Angular Velocity
- •14.3 Angular Acceleration
- •14.3.1 Example: Oscillating Antenna
- •14.4 Comparing Linear and Rotational Motion
- •14.5 Solving for the Rotational Motion
- •14.5.1 Example: Revolutions of an Accelerating Disc
- •14.5.2 Example: Angular Velocities of Two Objects in Contact
- •14.6 Rotational Motion in Three Dimensions
- •14.6.1 Example: Velocity and Acceleration of a Conical Pendulum
- •15 Rotation of Rigid Bodies
- •15.1 Rigid Bodies
- •15.2 Kinetic Energy of a Rotating Rigid Body
- •15.3 Calculating the Moment of Inertia
- •15.3.1 Example: Moment of Inertia of Two-Particle System
- •15.3.2 Example: Moment of Inertia of a Plate
- •15.4 Conservation of Energy for Rigid Bodies
- •15.4.1 Example: Rotating Rod
- •15.5 Relating Rotational and Translational Motion
- •15.5.1 Example: Weight and Spinning Wheel
- •15.5.2 Example: Rolling Down a Hill
- •16 Dynamics of Rigid Bodies
- •16.2.1 Example: Torque and Vector Decomposition
- •16.2.2 Example: Pulling at a Wheel
- •16.2.3 Example: Blowing at a Pendulum
- •16.3 Rotational Motion Around a Moving Center of Mass
- •16.3.1 Example: Kicking a Ball
- •16.3.2 Example: Rolling down an Inclined Plane
- •16.3.3 Example: Bouncing Rod
- •16.4 Collisions and Conservation Laws
- •16.4.1 Example: Block on a Frictionless Table
- •16.4.2 Example: Changing Your Angular Velocity
- •16.4.3 Example: Conservation of Rotational Momentum
- •16.4.4 Example: Ballistic Pendulum
- •16.4.5 Example: Rotating Rod
- •16.5 General Rotational Motion
- •Index
408 |
13 Multiparticle Systems |
start from a homogeneous disk, object AB, and remove a smaller circular portion, object B, and is left with a disk with a hole, object A.
The mass of the complete disk is MA B = π R2ρ, where ρ is the mass (area) density, and the mass of the small disk is MB = π r 2ρ. The subdivision principle states that the center of mass of the whole disk (object AB), which is at the origin, R = 0, can be written as:
MA B R = MA R A + MB R B . |
(13.24) |
=0
We solve this equation to Þnd R A , the unknown center of mass for object A.
R A = − |
MB |
π r 2ρ |
|
r 2 |
|
||
|
R B = − |
|
( R − r ) i = − |
|
( R − r ) i , |
(13.25) |
|
MA |
π R2ρ |
R2 |
|||||
Notice the simplicity of this approach. We did not have to perform any integration. This use of symmetries is a characteristic of physics that you will meet many times during your career.
13.2.3 Example: Center of Mass by Integration
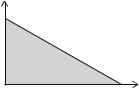
Problem: Find the center of mass of a thin, homogeneous triangular plate with sides of length a and b, as illustrated in Fig. 13.5. (You must be able to solve doubleintegrals to understand this example).
Solution: The center of mass for a continous, homogeneous object is deÞned as:
M R = r dm , (13.26)
m
where we have written the integral over the mass. Instead, we may integrate over space and use the mass (area) density, ρ:
M R = r ρ d A . (13.27)
A
Fig. 13.5 Illustration of a homogeneous triangle with sides of length a and b
y |
|
b |
|
a |
x |
13.2 The Center of Mass |
409 |
We need to Þnd both the mass, M , and the position R. Both are found by integration over the area A, which is the area of the triangle. First, we Þnd the mass by integrating over the area A. We integrate x from 0 to a, and y from 0 and up to the line corresponding to the upper boundary of the triangle. This is a line going through the points x = 0, y = b and x = a, y = 0. The straight line through these points has the equation y = b(1 − x /a).
M = |
A |
ρd A = ρ |
0 |
0 |
d y d x = ρ 0 |
b(1 − x /a) d x = |
2 ρab , |
|
|
|
|
a |
b(1−x /a) |
|
a |
1 |
|
|
|
|
|
|
|
|
(13.28) |
|
which, of course, is the well know formula for the area of a triangle multiplied with the mass density ρ of the triangle.
Now, we Þnd the position of the center of mass by calculating the integral for M R
for each component: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
M X = A xρd A = ρ 0 a 0 b(1−x /a) x d y d x = ρ 0 a x b(1 − x /a) d x |
(13.29) |
||||||||||||||||||||||||||||||||
1 |
|
|
|
1 |
a3b/a = ρ |
1 |
|
1 |
a2b |
|
1 |
|
|
||||||||||||||||||||
= ρ |
|
a2b − |
|
|
|
a2b − |
|
= ρ |
|
|
a2b , |
|
|||||||||||||||||||||
2 |
3 |
2 |
3 |
6 |
|
||||||||||||||||||||||||||||
The center of mass in the x -direction is therefore: |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
M X ρ (1/6) a2b 1 |
|
|
|
|
(13.30) |
|||||||||||||||||||
|
|
|
|
|
|
|
X = |
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
a . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ρ (1/2) ab |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
M |
3 |
|
|
|
|
|
|
||||||||||||||||
We use the same method in the y-direction: |
|
|
|
0 |
|
|
|
|
|
||||||||||||||||||||||||
M Y = A yρd A = ρ 0 |
0 |
|
|
|
y d y d x = ρ |
2 (b(1 − x /a))2 d x |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
a |
b(1−x |
/a) |
|
|
|
|
|
|
|
|
|
|
a |
1 |
|
|
|
|||||||||
= ρb2 2 |
1 |
u2(−1/a) du = ρb2 2 3 b2a , |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(13.31) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
which gives |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
Y = |
M Y ρ (1/6) b2a 1 |
b . |
|
|
|
|
(13.32) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
ρ (1/2) ab |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
M |
3 |
|
|
|
|
|
|
||||||||||||||||
The center of mass is therefore:
11
R = |
|
a i + |
|
b j . |
(13.33) |
|
|
||||
3 |
3 |
|
|
||
410 |
13 Multiparticle Systems |
13.2.4 Example: Center of Mass from Image Analysis
The center of mass is often used to describe the center of an object in an image . It may be because we are taking pictures of an object we want to track, such as the wandering behavior of a small grain of dust dancing through the air or the motion of a asteroid seen on the sky, or it may be to determine the center of mass of an irregularly shaped object.
How can we Þnd the center of mass from an image? First, we need to read the image so that we can access it. The image is taken from a classroom experiment, where we have extracted a smaller part of the image for analysis (see Fig. 7.4). We read the image ballimage02.png using:
Let us immediately display it to see if we got the right image:
subplot(1,2,1);
imshow(z)
axis(’equal’)
show()
where the axis commands are to clean up the plotted image. Notice that Python uses position [0,0] for the upper left part of the image, and that the Þrst coordinate is the vertical coordinate and the second coordinate is the horizontal coordinate, so that [iy,ix] is position [ix,iy] in the image. We call each (x , y) position for a pixel . We Þnd the size of the image using size:
>> shape(z2)
(411,559)
The image is stored as the matrix z(y, x , j ) which contain values of red (R, j = 1), green (G, j = 2), and blue (B, j = 3) . However, we cannot use these color values directly to Þnd the center of mass. Instead, we need to know if a pixel at (x , y) is a part of the object or not. We therefore set a threshold on the image, so that all pixels that are brighter than this threshold is included (set to value 1), and all the rest of the pixels are set to zero (Fig. 13.6):
z2 = (z[:,:,0]+z[:,:,1]+z[:,:,2])>1.5 subplot(1,2,2)
imshow(z2)
axis(’equal’)
The resulting images as shown in Fig. 13.7. The left image is the original image and the left image shows the Þltered image, where all the pixels that are part of the ball are colored red.
Now, we are ready to Þnd the center of mass:
|
1 |
|
1 |
|
(13.34) |
|
|
|
|
||||
X = |
|
xi , Y = |
|
yi |
||
M |
M |
|||||
|
i |
i |
|
|||
|
|
|
|
These formulas can be directly converted into an algorithm: For each pixel i , if the pixel is a part of the object, that is if z(xi , yi ) = 1, we include the positions xi and yi in the sum for the center of mass and include the pixel in the sum for the mass.

13.2 The Center of Mass |
411 |
|
|
|
|
|
|
|
Fig. 13.6 Image from video from classroom demonstration. The inset shows the image used for analysis
100 |
|
|
|
|
|
100 |
|
|
|
|
|
200 |
|
|
|
|
|
200 |
|
|
|
|
|
300 |
|
|
|
|
|
300 |
|
|
|
|
|
400 |
|
|
|
|
|
400 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
100 |
200 |
300 |
400 |
500 |
100 |
200 |
300 |
400 |
500 |
||
Fig. 13.7 Left Image of ball (cut). Right Filtered image of ball
s = shape(z2) x = 0
y = 0 m = 0
for iy in range(s[0]): for ix in range(s[1]):
if (z2[iy,ix]==1): x = x + ix
y = y + iy m = m + 1
xcm = x/m; ycm = y/m; hold(’on’)
plot(xcm,ycm,’kx’);
hold(’off’)
where we also plot the center of mass as an ÒxÓ. The last three lines ensure that empty pixels, pixels where z(x , y) = 0, are shown as white. (We set all three R,G,B values to 1 to generate a white entry in the colormap).
412 |
13 Multiparticle Systems |
This method is used for motion tracking of an image. If we are able to automatically Þlter the image so that we only get the object of interest, we can use this method to Þnd the center of mass of the object for each frame in a movie and thereby Þnd the center of mass as a function of time. Usually this requires careful positioning of the camera and a good choice of background for the Þlming.
13.3 Newton’s Second Law for Particle Systems
We have found that if we measure the position of a system of particles using the center of mass, R, of the system, the system behaves according to NewtonÕs second law:
Fext = M A , |
(13.35) |
where A is the acceleration of the center of mass of the system of particles, and the sum is over all external forces. This is true for any system of particles, from a galaxy consiting of starts, to the solar system, to a rigid body consiting of a large number of invididual atoms, down to a molecule or even an atom: The acceleration of the center of mass is given by the external forces acting on the system.
It is this law that allows us to use the techniques we have developed so far on any system, a solid body or a system of particles. In the previous chapters we have strictly speaking only discussed the motion of point-particles with a mass. We have always assumed that every part of a solid body has been moving with the same velocity. We have not allowed the object to oscillate, vibrate, change shape, or rotate. We have not allowed it to do any of the things that real objects do. However, we have now been saved by NewtonÕs second law for particle systems: If we measure the position of an object as the center of mass of the object, we can still use NewtonÕs second law to Þnd its motion, even if the object is vibrating, oscillating, rotating, or displaying other types of internal motion.
If I throw a ball through the room, we have previously found that the motion of the ball can be found from NewtonÕs second law for the ball:
F = G = −mg j = ma . |
(13.36) |
The beauty of NewtonÕs second law for particle systems is that we can use exactly the same analysis for a spinning or oscillating ball. The motion of the center of mass of the ball only depends on the external forces acting on the ball:
F = G = −mg j = mA . |
(13.37) |
It does not matter what happens internally in the ballÑif it is deformed, spinning, or vibratingÑthe motion of the center of the mass is the same as for a point particle as long as the external forces acting are the same.
