
- •Preface
- •Contents
- •1 Introduction
- •1.1 Physics
- •1.2 Mechanics
- •1.3 Integrating Numerical Methods
- •1.4 Problems and Exercises
- •1.5 How to Learn Physics
- •1.5.1 Advice for How to Succeed
- •1.6 How to Use This Book
- •2 Getting Started with Programming
- •2.1 A Python Calculator
- •2.2 Scripts and Functions
- •2.3 Plotting Data-Sets
- •2.4 Plotting a Function
- •2.5 Random Numbers
- •2.6 Conditions
- •2.7 Reading Real Data
- •2.7.1 Example: Plot of Function and Derivative
- •3 Units and Measurement
- •3.1 Standardized Units
- •3.2 Changing Units
- •3.4 Numerical Representation
- •4 Motion in One Dimension
- •4.1 Description of Motion
- •4.1.1 Example: Motion of a Falling Tennis Ball
- •4.2 Calculation of Motion
- •4.2.1 Example: Modeling the Motion of a Falling Tennis Ball
- •5 Forces in One Dimension
- •5.1 What Is a Force?
- •5.2 Identifying Forces
- •5.3.1 Example: Acceleration and Forces on a Lunar Lander
- •5.4 Force Models
- •5.5 Force Model: Gravitational Force
- •5.6 Force Model: Viscous Force
- •5.6.1 Example: Falling Raindrops
- •5.7 Force Model: Spring Force
- •5.7.1 Example: Motion of a Hanging Block
- •5.9.1 Example: Weight in an Elevator
- •6 Motion in Two and Three Dimensions
- •6.1 Vectors
- •6.2 Description of Motion
- •6.2.1 Example: Mars Express
- •6.3 Calculation of Motion
- •6.3.1 Example: Feather in the Wind
- •6.4 Frames of Reference
- •6.4.1 Example: Motion of a Boat on a Flowing River
- •7 Forces in Two and Three Dimensions
- •7.1 Identifying Forces
- •7.3.1 Example: Motion of a Ball with Gravity
- •7.4.1 Example: Path Through a Tornado
- •7.5.1 Example: Motion of a Bouncing Ball with Air Resistance
- •7.6.1 Example: Comet Trajectory
- •8 Constrained Motion
- •8.1 Linear Motion
- •8.2 Curved Motion
- •8.2.1 Example: Acceleration of a Matchbox Car
- •8.2.2 Example: Acceleration of a Rotating Rod
- •8.2.3 Example: Normal Acceleration in Circular Motion
- •9 Forces and Constrained Motion
- •9.1 Linear Constraints
- •9.1.1 Example: A Bead in the Wind
- •9.2.1 Example: Static Friction Forces
- •9.2.2 Example: Dynamic Friction of a Block Sliding up a Hill
- •9.2.3 Example: Oscillations During an Earthquake
- •9.3 Circular Motion
- •9.3.1 Example: A Car Driving Through a Curve
- •9.3.2 Example: Pendulum with Air Resistance
- •10 Work
- •10.1 Integration Methods
- •10.2 Work-Energy Theorem
- •10.3 Work Done by One-Dimensional Force Models
- •10.3.1 Example: Jumping from the Roof
- •10.3.2 Example: Stopping in a Cushion
- •10.4.1 Example: Work of Gravity
- •10.4.2 Example: Roller-Coaster Motion
- •10.4.3 Example: Work on a Block Sliding Down a Plane
- •10.5 Power
- •10.5.1 Example: Power Exerted When Climbing the Stairs
- •10.5.2 Example: Power of Small Bacterium
- •11 Energy
- •11.1 Motivating Examples
- •11.2 Potential Energy in One Dimension
- •11.2.1 Example: Falling Faster
- •11.2.2 Example: Roller-Coaster Motion
- •11.2.3 Example: Pendulum
- •11.2.4 Example: Spring Cannon
- •11.3 Energy Diagrams
- •11.3.1 Example: Energy Diagram for the Vertical Bow-Shot
- •11.3.2 Example: Atomic Motion Along a Surface
- •11.4 The Energy Principle
- •11.4.1 Example: Lift and Release
- •11.4.2 Example: Sliding Block
- •11.5 Potential Energy in Three Dimensions
- •11.5.1 Example: Constant Gravity in Three Dimensions
- •11.5.2 Example: Gravity in Three Dimensions
- •11.5.3 Example: Non-conservative Force Field
- •11.6 Energy Conservation as a Test of Numerical Solutions
- •12 Momentum, Impulse, and Collisions
- •12.2 Translational Momentum
- •12.3 Impulse and Change in Momentum
- •12.3.1 Example: Ball Colliding with Wall
- •12.3.2 Example: Hitting a Tennis Ball
- •12.4 Isolated Systems and Conservation of Momentum
- •12.5 Collisions
- •12.5.1 Example: Ballistic Pendulum
- •12.5.2 Example: Super-Ball
- •12.6 Modeling and Visualization of Collisions
- •12.7 Rocket Equation
- •12.7.1 Example: Adding Mass to a Railway Car
- •12.7.2 Example: Rocket with Diminishing Mass
- •13 Multiparticle Systems
- •13.1 Motion of a Multiparticle System
- •13.2 The Center of Mass
- •13.2.1 Example: Points on a Line
- •13.2.2 Example: Center of Mass of Object with Hole
- •13.2.3 Example: Center of Mass by Integration
- •13.2.4 Example: Center of Mass from Image Analysis
- •13.3.1 Example: Ballistic Motion with an Explosion
- •13.4 Motion in the Center of Mass System
- •13.5 Energy Partitioning
- •13.5.1 Example: Bouncing Dumbbell
- •13.6 Energy Principle for Multi-particle Systems
- •14 Rotational Motion
- •14.2 Angular Velocity
- •14.3 Angular Acceleration
- •14.3.1 Example: Oscillating Antenna
- •14.4 Comparing Linear and Rotational Motion
- •14.5 Solving for the Rotational Motion
- •14.5.1 Example: Revolutions of an Accelerating Disc
- •14.5.2 Example: Angular Velocities of Two Objects in Contact
- •14.6 Rotational Motion in Three Dimensions
- •14.6.1 Example: Velocity and Acceleration of a Conical Pendulum
- •15 Rotation of Rigid Bodies
- •15.1 Rigid Bodies
- •15.2 Kinetic Energy of a Rotating Rigid Body
- •15.3 Calculating the Moment of Inertia
- •15.3.1 Example: Moment of Inertia of Two-Particle System
- •15.3.2 Example: Moment of Inertia of a Plate
- •15.4 Conservation of Energy for Rigid Bodies
- •15.4.1 Example: Rotating Rod
- •15.5 Relating Rotational and Translational Motion
- •15.5.1 Example: Weight and Spinning Wheel
- •15.5.2 Example: Rolling Down a Hill
- •16 Dynamics of Rigid Bodies
- •16.2.1 Example: Torque and Vector Decomposition
- •16.2.2 Example: Pulling at a Wheel
- •16.2.3 Example: Blowing at a Pendulum
- •16.3 Rotational Motion Around a Moving Center of Mass
- •16.3.1 Example: Kicking a Ball
- •16.3.2 Example: Rolling down an Inclined Plane
- •16.3.3 Example: Bouncing Rod
- •16.4 Collisions and Conservation Laws
- •16.4.1 Example: Block on a Frictionless Table
- •16.4.2 Example: Changing Your Angular Velocity
- •16.4.3 Example: Conservation of Rotational Momentum
- •16.4.4 Example: Ballistic Pendulum
- •16.4.5 Example: Rotating Rod
- •16.5 General Rotational Motion
- •Index
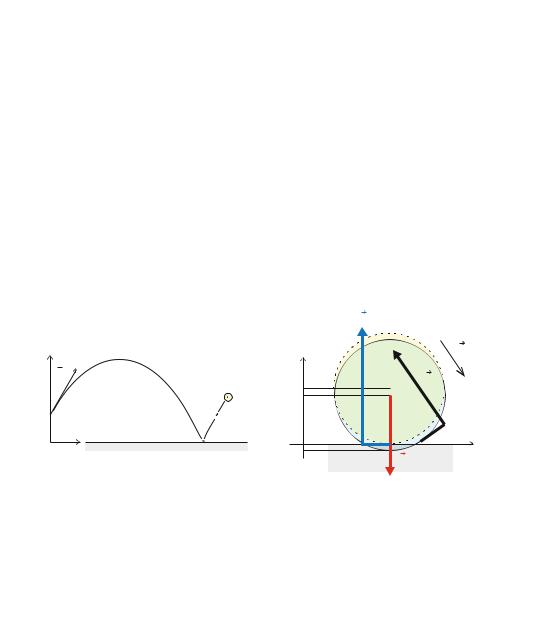
7.5 Force Model—Spring Force |
201 |
7.5.1 Example: Motion of a Bouncing Ball with Air Resistance
In this example we study the motion of an object subject to a constant force, a velocitydependent force, and a position-dependent force. We solve the problem numerically and discuss the results following a workflow similar to what you will find in many practical problems.
Let us continue to refine the description of a ball thrown in the classroom. So far we have introduced gravity and air resistance. But what happens when the ball hits the floor? We need to also include a force model for the normal force from the floor on the ball. The simplest approach to such a contact force model is a spring model: We model the interaction between the floor and the ball as a single spring. But the normal force is zero when there is no contact. In this problem we demonstrate how to include such effects in our models.
Problem: A ball is thrown from a height h above the ground with an initial velocity v0. Find the velocity and position of the ball as a function of time t . Include the normal force from the floor while the ball is in contact with the floor.
Identify and Sketch: We describe the position of the ball by r(t ), measured in a coordinate system with origin at the floor. The initial position and velocity of the projectile is r(t0) = h j and v(t0) = v0 = vx ,0 i + vy,0 j.
Model: The motion of the ball is determined by the forces acting: air resistance, FD , the normal force N from the floor, and gravity, G = −mg j, as illustrated in the free-body diagram in Fig. 7.10. We use a square law for air resistance:
FD = −Dvv . |
(7.47) |
The normal force from the floor on the ball is represented by a spring force. This is a strong simplification of the actual deformation process occurring at the contact between the ball and the floor due to the deformation of both the ball and the floor.
(A) |
N |
(B) |
|
y |
v |
y |
|
v0 |
FD |
|
|
|
y |
h |
|
x |
x |
|
G |
Fig. 7.10 a Sketch of the path of the ball. b Free-body diagram for the ball when in contact with the floor
202 7 Forces in Two and Three Dimensions
The deformed region corresponds roughly to the region of “overlap” between the ball and the floor in Fig. 7.10. The depth of this region is y = R − y(t ), where R
is the radius of the ball, which corresponds to the compression |
L of the spring: |
N = −k ( R − y(t )) j . |
(7.48) |
We check that the sign is correct: The normal force must act upward when y < R, hence the sign must be negative.
However, we must also ensure that the normal force only acts when the ball is in contact with the floor, otherwise the normal force is zero. The full formation of the
normal force is therefore: |
|
|
|
|
|
N = |
|
0 |
when y(t ) ≥ R . |
(7.49) |
|
|
|
−k ( R − y(t )) j |
when y(t ) < |
R |
|
Newton’s second law: Newton’s second law is now |
|
|
|||
|
|
|
|
|
|
|
|
F j = G + FD + N = ma , |
|
(7.50) |
|
|
|
j |
|
|
|
which gives |
|
|
|
|
|
|
a = − ( D/m) v v − g j + N/m , |
|
(7.51) |
||
with the initial conditions: r(t0) = r(0 s) = r0 and v(t0) = v(0 s) = v0. While it is difficult to determine the motion analytically, we may be able to find analytical solutions for parts of the motion. However, we can determine the motion numerically by integrating (7.51) using Euler-Cromer’s method:
|
v(ti + |
t ) v(ti ) + |
t a(ti , r(ti ), v(ti )) |
(7.52) |
|
r(ti + |
t ) r(ti ) + |
t v(ti + t ) . |
(7.53) |
The implementation is straight-forward: |
|
|
||
from pylab import * |
|
|
|
|
m = 0.2 |
# kg |
|
|
|
g = 9.81 |
# m/sˆ2 |
|
|
|
vT = 20.0 |
# m/s |
|
|
|
h = 2.0 |
# m |
|
|
|
R = 0.1 |
# m |
|
|
|
k = 1000.0 |
# N/m |
|
|
|
r0 = array([0.0,h]) |
|
|
|
|
v0 = array([10.0,10.0]) |
|
|
|
|
time = 20.0 |
# s |
|
|
|
dt = 0.001 |
# |
|
|
|
s n = int(round(time/dt)) r = zeros((n,2),float)
v = zeros((n,2),float) t = zeros(n,float) r[0] = r0
v[0] = v0
7.5 Force Model—Spring Force
Fig. 7.11 Plot of the trajectory of the ball calculated using Euler-Cromers method for quadratic air resistance (solid line), compared with the trajectory without air resistance (dashed line)
y [M]
203
6
4 

2 
0 |
|
|
|
0 |
5 |
10 |
15 |
x [M]
t[0] = 0.0
# Simulation loop for i in range(n): if (r[i,1]<R):
N = k*(R-r[i,1])*array([0,1]) else:
N = array([0,0])
FD = - D*norm(v[i])*v[i] G = -m*g*array([0,1]) Fnet = N + FD + G
a = Fnet/m
v[i+1] = v[i] + a*dt r[i+1] = r[i] + v[i+1]*dt t[i+1] = t[i] + dt
plot(r[:,0],r[:,1])
xlabel(’x [m]’), ylabel(’y [m]’)
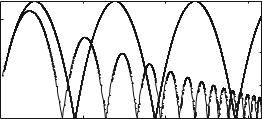
where we have used the vT = 10.0 m/s to calculate D, and m = 0.2 kg. We have chosen to use the spring constant k = 1000 N/m, a number we have largely guessed for now. (The effective spring constant may be measured by experiment or calculated if we know the material properties of the ball and the floor). The resulting path is illustrated in Fig. 7.11, where it is compared with the path of the ball without air resistance.
Detailed analysis of wall contact: While the behavior in Fig. 7.11 looks reasonable at first, a closer examination shows that something is wrong, at least according to our intuition. When there is no air resistance, the ball bounces back to the same height! We know that a real ball would not behave like this. What is wrong?
Figure 7.12 shows a magnification of the behavior of the ball during a bounce when there is no air resistance. The red lines in the figures mark the positions and the times when the ball comes in contact with the floor. We see that the horizontal velocity, vx , does not change at all during the bounce. This is not surprising, since the normal force only has a vertical component. No horizontal forces means no horizontal acceleration. However, we also see that the vertical velocity component, vy , simply reverses during the bounce. This is the part that strikes us as unrealistic. And indeed it is. How can we modify the force model for the normal force to ensure that the vertical speed is smaller after the collision? This question we will return to later when we discuss energy and collisions. The short answer is that we need to introduce a force that is velocity dependent: Any force model that only depends on

204
0.2 |
|
|
|
|
|
||
[M ] |
|
|
|
|
|
|
|
0.1 |
|
|
|
y |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.6 |
||
[M /S ] |
3 |
|
|
|
|
||
2 |
|
|
|
|
|
||
X |
|
|
|
v |
|
|
|
|
1 |
|
|
|
|
|
|
|
20 |
|
|
[M /S ] |
0 |
|
|
|
|
||
Y |
|
|
|
v |
|
|
|
−20
7 Forces in Two and Three Dimensions
3.8 |
4 |
4.2 |
4.4 |
4.6 |
4.8 |
5 |
5.2 |
x [M ]
2.21 |
2.22 |
2.23 |
2.24 |
2.25 |
2.26 |
t [S ]
2.21 |
2.22 |
2.23 |
2.24 |
2.25 |
2.26 |
t [S ]
Fig. 7.12 Plot of the trajectory of the ball without air resistance during its collision with the floor. The red lines illustrates the points where the ball comes in contact with the floor
the vertical position y(t ) of the ball will always result in a reversal of the velocity! By introducing a viscous force, a linear velocity dependent force model, during the collision with the floor, the outgoing vertical velocity will be reduced. But more on this later! (See Chap. 12.)
Comments: We have now built a model for a bouncing ball, including both air resistance and a normal force from the floor. You should notice the simple structure followed systematically: as long as we can develop force models for the interactions, we can model the motion. This method is robust and no different in one-, two-, or three dimensions. You should also notice that the normal force changes: It does not always just balance the gravitational force—it is indeed larger than the gravitational force in parts of the collision. Otherwise the normal force would not be able to change the direction of the ball. This simple point is a clear result of the force model approach, and also of a careful physical analysis, but represents a classical misunderstanding.
