
- •Введение
- •Глава 1. ОСновные понятия теории множеств, комплексных чисел и алгебры многочленов
- •1. Элементы теории множеств и комплексных чисел
- •1.1. Понятие множества. Операции над множествами
- •1.2. Числовые множества и их свойства.
- •2. Алгебра многочленов.
- •Глава 2. Матрицы. Определители
- •1. Алгебра матриц.
- •Виды матриц.
- •2. Определитель n-го порядка.
- •2.1. Определение. Вычисление определителей 2 и 3-го порядков.
- •2.2.Миноры и алгебраические дополнения.
- •2.3.Свойства определителя n-го порядка.
- •3. Действия над матрицами.
- •3.1. Линейные операции над матрицами.
- •3.2. Умножение матриц.
- •3.3. Многочлены от матриц.
- •3.4. Обратная матрица.
- •Вычисление обратной матрицы (через алгебраические дополнения).
- •3.5. Линейная зависимость строк и столбцов матрицы.
- •3.6. Ранг матрицы. Базисный минор.
- •3.7 Нахождение ранга матрицы
- •Вопросы для повторения.
- •Глава 3. Системы линейных уравнений и методы их решения.
- •1. Основные понятия и определения
- •2. Условия совместности системы линейных уравнений
- •3. Метод обратной матрицы
- •4. Правило Крамера
- •5. Метод Гаусса исключения неизвестных
- •7. Метод полного исключения
- •7.1. Решение систем линейных уравнений
- •7.2. Вычисление обратной матрицы методом полного исключения.
- •7.3. Вычисление ранга матрицы методом полного исключения
- •Линейное пространство.
- •8. Собственные значения и собственные векторы матриц
- •9. Квадратичные формы
- •10. Численные методы решения систем линейных уравнений
- •Вопросы для повторения.
- •Задачи для самостоятельного решения.
- •Глава 4. Векторная алгебра
- •Векторное произведение двух векторов.
- •Вопросы для повторения.
- •Глава 5. Задачи линейного программирования
- •1. Постановка задачи линейного программирования (злп)
- •2. Графический метод решения злп
- •3. Симплекс – метод решения злп
- •4. Двойственные злп
- •Методы определения опорного плана тз.
- •Вопросы для повторения.
- •Глава 6. Балансовые модели
- •1. Экономико-математическая модель (эмм) межотраслевого стоимостного баланса (модель Леонтьева)
- •Модель международной торговли
- •Вопросы для повторения.
- •Задачи для самостоятельного решения.
- •Библиографический список
- •Глава 1. ОСновные понятия теории множеств, комплексных чисел и алгебры многочленов 4
- •Глава 2. Матрицы. Определители 17
- •Глава 3. Системы линейных уравнений и методы их решения. 52
- •Глава 4. Векторная алгебра 103
- •Глава 5. Задачи линейного программирования 118
- •Глава 6. Балансовые модели 153
- •394026 Воронеж, Московский просп., 14
Вопросы для повторения.
Вектор. Модуль вектора. Нулевой и единичный векторы. Коллинеарные, компланарные, равные, противоположные векторы,
Линейные операции над векторами и их свойства.
Геометрическая проекция вектора на ось (направление) и её свойства. Алгебраическая проекция.
Векторы в декартовой системе координат.
Скалярное произведение векторов и его свойства.
Векторное произведение векторов, его геометрический смысл и свойства. Координаты векторного произведения. Двойное векторное произведение.
Смешанное произведение векторов, его геометрический смысл и свойства.
Определение евклидова векторного пространства Rn.
Линейно зависимые и независимые системы векторов. Ранг системы векторов. Диагональная система векторов. Теорема о разложении вектора по базису. Ортогональный, ортонормированный, единичный базисы.
Задачи для самостоятельного решения.
На векторах
 и
и
 построить треугольник OAB. Точка М делит
сторону отрезка АВ в отношении 2:3. Найти
координаты вектора
построить треугольник OAB. Точка М делит
сторону отрезка АВ в отношении 2:3. Найти
координаты вектора
 .
.Построить треугольник с вершинами А(2,-3,1), В(4,11,6), С(4,-4,3). Найти длины сторон АС, АВ и угол ВАС.
Построить параллелограмм на векторах
 и
и
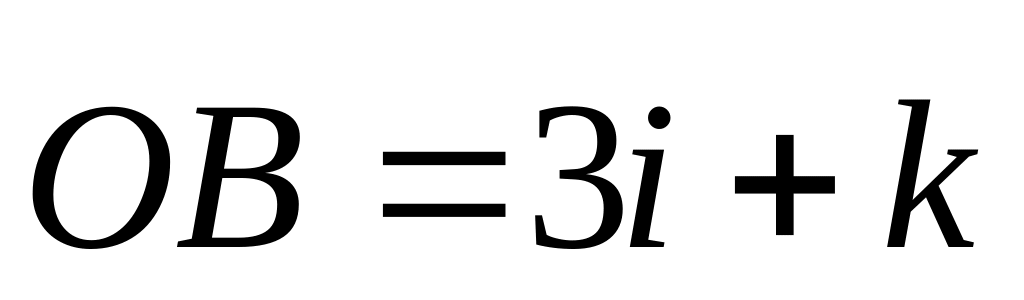 .
Определить острый угол между диагоналями
параллелограмма.
.
Определить острый угол между диагоналями
параллелограмма.Даны векторы
 и
и
 .
Найти вектор
.
Найти вектор
 ,
ортогональный
,
ортогональный
 и
и
 ,
если его длина равна
,
если его длина равна


 Найти
Найти

 .
.В пространстве даны 4 точки: А(1,1,1), В(4,4,4), С(3,5,5), D(2,4,7). Найти объём тетраэдра АВСD.
Показать, что векторы


 линейно зависимы. Найти эту
зависимость.
линейно зависимы. Найти эту
зависимость.Для системы векторов из задачи 1 найти все базисы.
Определить ранг системы векторов:


 ,
, .
.Векторы


 образуют базис в R3.
Разложить по этому базису вектор
образуют базис в R3.
Разложить по этому базису вектор
 .
.Найти векторы, дополняющие следующие системы до ортонормированных базисов:
a)

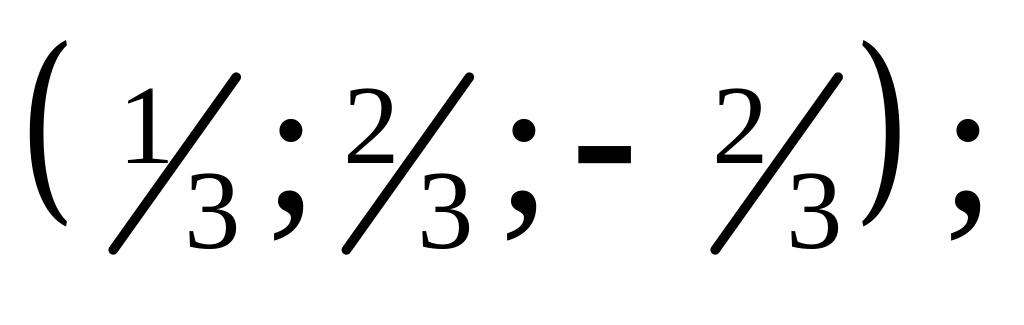
б)


Даны ортонормированные векторы
 ,и
,и
 Подобрать третий вектор
так, чтобы система
,
,
образовала ортонормированный базис.
Подобрать третий вектор
так, чтобы система
,
,
образовала ортонормированный базис.Показать, что векторы
 ,
, ортогональны. Дополнить систему
,
до ортогонального базиса. Найти
координаты вектора
ортогональны. Дополнить систему
,
до ортогонального базиса. Найти
координаты вектора
 в этом базисе.
в этом базисе.Векторы


 образуют ортонормированный базис.
Найти в этом базисе координаты вектора
образуют ортонормированный базис.
Найти в этом базисе координаты вектора

Показать, что векторы


 образуют базис в R3.
Разложить вектор
образуют базис в R3.
Разложить вектор
 по этому базису.
по этому базису.
Глава 5. Задачи линейного программирования
1. Постановка задачи линейного программирования (злп)
Линейное программирование - наука о методах исследования и отыскания экстремальных (наибольших и наименьших) значений линейной функции, на неизвестные которой наложены линейные ограничения.
Эта линейная функция называется целевой, а ограничения, которые математически записываются в виде уравнений или неравенств, называются системой ограничений. Математическое выражение целевой функции и её ограничений называется математической моделью задачи.
В общем виде ЗЛП ставится следующим образом (общая ЗЛП): найти максимум (минимум) функции
![]() (1)
(1)
при ограничениях
 (2)
(2)
где
![]() (
(![]() )
- управляющие переменные или решения
задачи
)
- управляющие переменные или решения
задачи
(1)-(2), аij,
bi,
сj, i=![]() ,
j=
,
j=![]() ,
- заданные числа (параметры), F-целевая
функция или критерий эффективности
(оптимальности) задачи.
,
- заданные числа (параметры), F-целевая
функция или критерий эффективности
(оптимальности) задачи.
Функция (1) - линейная, ограничения (2) - линейные. Задача содержит n переменных и m ограничений.
Решить ЗЛП - это значит найти значения управляющих переменных xj, j= , удовлетворяющих ограничения (2), при которых целевая функция (1) принимает экстремальное значение.
Основной
(канонической) ЗЛП называется задача,
состоящая в определении максимума
целевой функции при ограничениях,
заданных равенствами и
![]() .
.
Допустимым решением (планом) ЗЛП называется вектор X=(x1, x2, …, xn), удовлетворяющий системе ограничений (2). Множество допустимых решений образует область допустимых решений (ОДР).
Допустимое
решение Х*=![]() ,
при котором целевая функция достигает
своего экстремального значения,
называется оптимальным решением
ЗЛП.
,
при котором целевая функция достигает
своего экстремального значения,
называется оптимальным решением
ЗЛП.
