
- •Введение
- •Глава 1. ОСновные понятия теории множеств, комплексных чисел и алгебры многочленов
- •1. Элементы теории множеств и комплексных чисел
- •1.1. Понятие множества. Операции над множествами
- •1.2. Числовые множества и их свойства.
- •2. Алгебра многочленов.
- •Глава 2. Матрицы. Определители
- •1. Алгебра матриц.
- •Виды матриц.
- •2. Определитель n-го порядка.
- •2.1. Определение. Вычисление определителей 2 и 3-го порядков.
- •2.2.Миноры и алгебраические дополнения.
- •2.3.Свойства определителя n-го порядка.
- •3. Действия над матрицами.
- •3.1. Линейные операции над матрицами.
- •3.2. Умножение матриц.
- •3.3. Многочлены от матриц.
- •3.4. Обратная матрица.
- •Вычисление обратной матрицы (через алгебраические дополнения).
- •3.5. Линейная зависимость строк и столбцов матрицы.
- •3.6. Ранг матрицы. Базисный минор.
- •3.7 Нахождение ранга матрицы
- •Вопросы для повторения.
- •Глава 3. Системы линейных уравнений и методы их решения.
- •1. Основные понятия и определения
- •2. Условия совместности системы линейных уравнений
- •3. Метод обратной матрицы
- •4. Правило Крамера
- •5. Метод Гаусса исключения неизвестных
- •7. Метод полного исключения
- •7.1. Решение систем линейных уравнений
- •7.2. Вычисление обратной матрицы методом полного исключения.
- •7.3. Вычисление ранга матрицы методом полного исключения
- •Линейное пространство.
- •8. Собственные значения и собственные векторы матриц
- •9. Квадратичные формы
- •10. Численные методы решения систем линейных уравнений
- •Вопросы для повторения.
- •Задачи для самостоятельного решения.
- •Глава 4. Векторная алгебра
- •Векторное произведение двух векторов.
- •Вопросы для повторения.
- •Глава 5. Задачи линейного программирования
- •1. Постановка задачи линейного программирования (злп)
- •2. Графический метод решения злп
- •3. Симплекс – метод решения злп
- •4. Двойственные злп
- •Методы определения опорного плана тз.
- •Вопросы для повторения.
- •Глава 6. Балансовые модели
- •1. Экономико-математическая модель (эмм) межотраслевого стоимостного баланса (модель Леонтьева)
- •Модель международной торговли
- •Вопросы для повторения.
- •Задачи для самостоятельного решения.
- •Библиографический список
- •Глава 1. ОСновные понятия теории множеств, комплексных чисел и алгебры многочленов 4
- •Глава 2. Матрицы. Определители 17
- •Глава 3. Системы линейных уравнений и методы их решения. 52
- •Глава 4. Векторная алгебра 103
- •Глава 5. Задачи линейного программирования 118
- •Глава 6. Балансовые модели 153
- •394026 Воронеж, Московский просп., 14
7. Метод полного исключения
Используется для решения систем линейных уравнений, обращения матриц, разложения вектора по базису, вычисления ранга матрицы.
7.1. Решение систем линейных уравнений
Первый шаг (соответствует исключению неизвестной x1) выполняется с разрешающим элементом a110 по правилам прямого хода метода Гаусса.
Общий шаг (соответствует последовательному исключению неизвестных x2, x3, ..., xn) выполняется по следующим правилам:
назначается разрешающий элемент; им будет коэффициент при исключаемой неизвестной;
элементы разрешающей строки остаются неизменными;
все элементы разрешающего столбца (кроме разрешающего элемента) заменяются нулями и остаются таковыми до конца преобразований;
все прочие элементы пересчитываются по правилу прямоугольника.
Контроль вычислений остается неизменным.
Решим ту же самую систему линейных уравнений методом полного исключения.




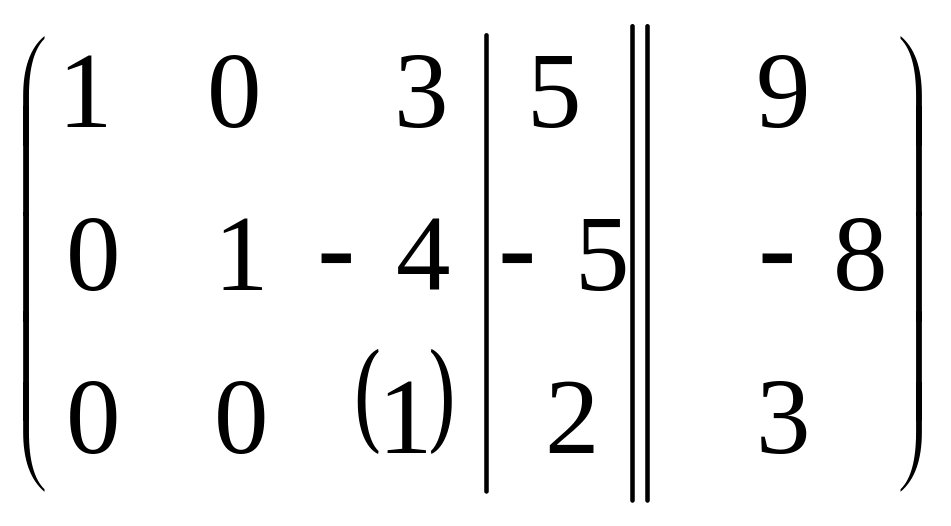

Ответ:
![]() .
.
7.2. Вычисление обратной матрицы методом полного исключения.
Дана
матрица
 ,
det
A
0.
,
det
A
0.
Составляем расширенную матрицу, приписав справа к исходной матрице единичную матрицу, отделив её от исходной вертикальной чертой:
 .
.
Эта матрица подвергается преобразованиям по алгоритму полного исключения и слева от вертикальной черты получается единичная, а справа - обратная матрица А-1. При расчёте желательно вести контроль вычислений.
Пример.
Для матрицы А= найти А-1,
пользуясь методом полного исключения.
найти А-1,
пользуясь методом полного исключения.
Решение.


 ~
~ ~
~
 ~
~
А-1= =
= .
.
7.3. Вычисление ранга матрицы методом полного исключения
Пусть дана матрица A размеров m x n. Если в ходе преобразований её методом полного исключения не встретится строка (столбец), состоящая сплошь из нулей, то rang A = min(m;n). Если же k (k<min(m;n)) строк (столбцов) матрицы окажутся состоящими сплошь из нулей, то rang A = min(m;n)-k.
Пример. Найти ранг матрицы:
A=![]()
Решение.




![]()
Следовательно, rang A=2.
Однородные системы линейных уравнений.
Определение. Система линейных уравнений называется однородной, если во всех её уравнениях свободные члены равны 0.
В общем случае однородная система имеет вид:
 .
.
Однородная
система всегда совместна, т.к. имеет
нулевое (тривиальное)
решение xi=0,
i=![]() .
.
Теорема 1. Однородная система, в которой число уравнений меньше числа неизвестных, всегда имеет ненулевое решение.
Теорема 2. Если в однородной системе число уравнений равно числу неизвестных, то она имеет ненулевое решение тогда и только тогда, когда определитель матрицы системы равен 0.
Пусть
![]() - множество всех решений однородной
системы. Всякий базис в множестве
- множество всех решений однородной
системы. Всякий базис в множестве
![]() состоит из
состоит из
![]() векторов
векторов
![]() .
Соответствующая ему в базисе система
вектор-столбцов
.
Соответствующая ему в базисе система
вектор-столбцов
![]() называется фундаментальной
системой решений.
Общее решение однородной системы имеет
вид
называется фундаментальной
системой решений.
Общее решение однородной системы имеет
вид
![]() ,
,
где
![]() - произвольные постоянные.
- произвольные постоянные.
Пример. Найти общее решение и проанализировать его структуру (указать базис пространства решений однородной системы, установить размерность пространства)

Решение. Преобразуем матрицу коэффициентов
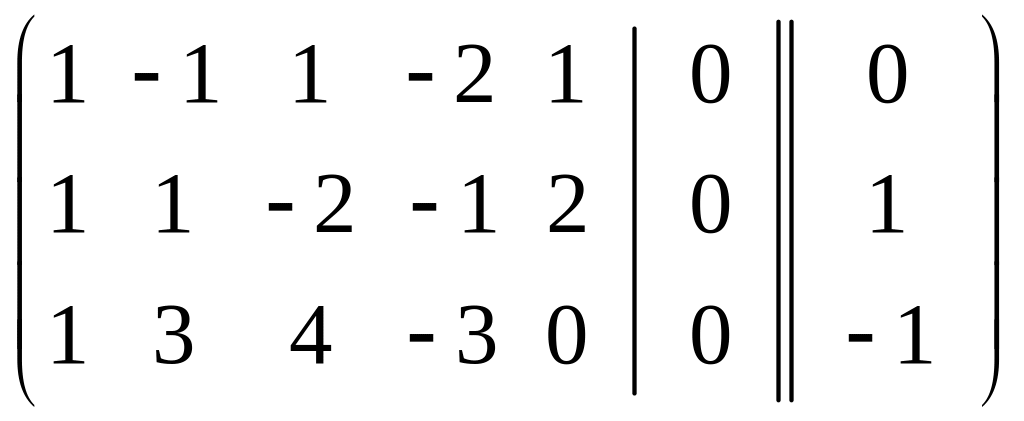


 .
.

Следовательно,
![]() - базис. Размерность пространства решения
- базис. Размерность пространства решения
![]() .
Полагая
.
Полагая
![]()
![]()
![]() получим общее решение системы
получим общее решение системы
 .
.
Из общего решения находим фундаментальную систему решений (частное решение):
 ,
,
 ,
,
 .
.
С
использованием фундаментальной системой
решений может быть записано в виде
![]() .
.
