
862
.pdf
81
Изменение скорости воздуха, обтекающего вокруг семян, может вызвать эффект дополнительного увеличения присасывающей силы, подобно тому, как увеличивается подъемная сила крыла самолета.
Взаимодействие семян с воздушным потоком и не только в зоне присасывания, но и на участках транспортирования, зависит не только от перепада давления, но и от его скорости, условий обтекания семян воздухом, конфигурации «истоков», «стоков», профиля воздуховода, наличия эжекторных и байпасных устройств. Иными словами, сколько-нибудь корректный подход к анализу взаимодействия семян с воздухом требует детального исследования движения многочисленных элементов этой среды в поле внешних сил.
Наиболее полно макроскопические движения твердых, жидких и газообразных сред в поле внешних сил изучается в одном из разделов теоре-
тической физики – механике сплошных сред (МСС) [4.4], [4.8], [4.11].
Используемые в МСС уравнения состояния среды позволяют проследить за изменениями плотности, массы, векторов перемещения и скорости среды, тензоров внутренних напряжений, деформаций и скоростей деформаций, кинетической, внутренней энергии и энтропии [4.1], [4.2], [4.3],
[4.5].
Таким образом, методы механики сплошной среды могут быть базой разработки общей теории работы высевающих аппаратов различного принципа действия.
Основой для уравнений, описывающих течение воздуха около семян, могут служить уравнения механики сплошной среды:
1. Закон сохранения массы газа
d ( d ) 0 , dt
приводящий к уравнению неразрывности потока
д div(V ) 0 .
дt
2. Закон сохранения количества движения
Q Vd ,
и уравнение изменения количества движения
dQ |
F Pn . |
||
dt |
|||
|
|
||
|
|||
3.Основное уравнение динамики сплошной среды
dVdt F DivР .
4.Уравнение баланса энергии сплошной среды
|
d |
V 2 |
|
|
|
|
|
|
|
|
FV div(PV ) q . |
|
|
||||
|
U |
|
|
||
|
dt |
2 |
|
|
|
(4.3)
(4.4)
(4.5)
(4.6)
(4.7)
(4.8)
82 |
|
5. Зависимость плотности среды от давления |
|
Р . |
(4.9) |
В этих уравнениях использованы следующие обозначения:
- плотность среды; и - соответственно, элементарный объем и его поверхность; Рн и F – плотность поверхностных и массовых сил; Р– тензор напряжений в среде газа; U – удельная внутренняя энергия среды; q – удельное количество энергии, подведенной извне.
Основное уравнение динамики сплошной среды (4.7) может быть представлено в проекциях на оси прямоугольной декартовой системы координат.
Учитывая выражения проекций ускорения в эйлеровых переменных и проекций тензора DivP,
|
|
|
|
|
|
|
|
|
|
|
|
(DivP) |
i |
Pki ,i 1,2,3, |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
можно получить |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
V |
|
|
|
V |
|
|
V |
|
|
|
V |
|
P |
|
|
Pyx |
|
P |
||||||||||||
|
|
( |
|
|
x V |
|
x V |
|
|
x V |
|
x ) F |
|
|
xx |
|
|
|
|
|
|
zx |
||||||||||||
|
|
t |
|
|
|
|
|
x |
|
y |
|
z |
||||||||||||||||||||||
|
|
|
|
|
|
x |
x |
|
y |
y |
|
|
z z |
x |
|
|
|
|
|
|
|
|||||||||||||
|
|
( |
Vy |
V |
Vy |
V |
|
Vy |
V |
|
Vy |
) F |
|
Pxy |
|
|
|
Pyy |
|
|
Pzy |
|
||||||||||||
|
|
|
|
|
|
|
|
|
x |
|
y |
|
z |
|||||||||||||||||||||
|
|
|
|
t |
|
|
|
x |
x |
|
y |
y |
|
|
z z |
y |
|
|
|
|
|
|
|
|||||||||||
|
V |
|
|
|
V |
|
|
V |
|
|
|
V |
|
|
|
|
P |
|
|
Pyz |
|
|
|
P |
|
|
|
|
||||||
( |
|
z V |
|
|
z |
V |
|
|
z V |
|
|
z ) |
F |
xz |
|
|
|
|
|
zz |
|
(4.10) |
||||||||||||
t |
|
x |
|
|
|
|
|
|
y |
|
z |
|
||||||||||||||||||||||
|
|
|
x |
|
|
|
y y |
|
|
z z |
|
|
z |
x |
|
|
|
|
|
|
|
|
|
|||||||||||
К этим соотношениям присоединяют еще одно динамическое уравнение (4.4) неразрывности потока. Выразив оператор div(V) в прямоугольных декартовых координатах, уравнение приобретает вид:
|
|
( V ) |
|
( Vy ) |
|
( V ) |
) 0 . |
|
|
|
x |
|
z |
(4.11) |
|||||
t |
x |
y |
z |
||||||
|
|
|
|
|
Эти уравнения содержат 13 неизвестных: (элементы тензора Pxx, Pyx,
Pxz, Pxy, Pyy, Pzy, Pxz, Pyz, Pzz, составляющие скорости Vx, Vy, Vz, и ) т.е. представляют собой незамкнутую систему.
Для замыкания этой системы используют обычно те или иные допущения о математических моделях среды: идеально упругая среда, подчиняющаяся линейному закону Гука, идеальная жидкость, лишенная внутреннего трения, вязкая жидкость, движение которой описывается законом Ньютона и т.д.
Разумеется, использование той или иной модели, идеализирующей реальный процесс, может привести к ошибкам, что ставит задачу об их оценке.
При сравнительно низких скоростях движения воздух чаще всего
представляют в виде идеальной жидкости. |
|
В этом случае |
|
Рху Рух Руz Pzy Pxz Pzx 0 |
|
Pxx Pyy Pzz P(давление в среде) |
(4.12) |
83
Уравнение динамики (4.7) в проекциях на оси координат в этом случае преобразуется к виду
|
|
дVx |
|
V |
|
|
|
дVx |
|
V |
|
|
|
дVx |
|
V |
|
|
дVx |
|
F |
1 дР |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
x дx |
y дy |
z дz |
дх |
|
|||||||||||||||||||||||||||||
|
|
дt |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|||||||||||||||||||||
|
дVy |
|
V |
|
дVy |
V |
|
|
|
дVy |
|
V |
|
|
дVy |
|
F |
|
|
1 дР |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
дt |
x дx |
y дy |
|
z дz |
|
y |
дy |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
дVz |
V |
|
|
|
дVz |
V |
|
|
|
дVz |
|
|
V |
|
|
дVz |
|
|
F |
|
|
|
1 дР |
(4.13) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
x дx |
y дy |
|
z дz |
|
|
|
дz |
||||||||||||||||||||||||||
|
|
дt |
|
|
|
|
|
|
|
|
|
z |
|
|
|
|||||||||||||||||||||
|
|
|
|
д |
|
|
|
д( V |
) |
|
д( Vy ) |
|
д( V |
) |
0 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
||||||||||||
|
|
|
|
дt |
|
|
дx |
|
дy |
|
|
|
|
|
дz |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
(P) |
уравнение баротропности |
|
||||||||||||||||||||||||||||||||
Если = const, то жидкость несжимаема, а в случае |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
k const , |
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.14) |
|||||||||||||
где k – показатель адиабаты, движение среды считают адиабатическим. Обычно несжимаемыми признают капельные жидкости.
При идеализации движения воздуха отказ от учета его сжимаемости представляется чрезмерным.
Оценка возможных ошибок может быть осуществлена решением задачи об одномерном распространении малых возмущений в неподвижном газе [4.10].
Пусть вдоль оси Ох некоторой трубки покоится газ с параметрами Р0,0 и скоростью V0 = 0.
Если в газе создать небольшие возмущения этих параметров, то
р Р Р'; 0 '; Vx V0 V ' V ' .
При постановке этих значений в уравнения (4.13), предварительно оговаривают, что при допущении о баротропности движения (заключающейся в зависимости плотности только от давления Р, но не от температуры) будет соблюдаться равенство
дР |
|
dР |
|
д |
dР |
д ' |
|
|||
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|||||
дх |
|
d |
|
дх |
d 0 |
дх |
|
|||
Причем, с повышением давления возрастает и плотность позволяет предположить:
dP |
а2 . |
||
|
|
|
|
|
|||
d 0 |
0 |
||
|
|||
(4.15)
dР / d 0 , что
(4.16)
Пренебрегая малыми величинами второго порядка и опуская объемную силу, можно прийти к линейной системе уравнений:
|
|
дV ' |
a2 |
д |
' |
; |
|
дV ' |
|
д |
' |
. |
(4.17) |
||
|
|
|
|
|
|
|
|
|
|
||||||
|
0 дt |
0 |
дx |
|
|
0 |
дx |
|
дt |
|
|
|
|||

84
Исключив из этих равенств систему (4.17), можно свести к так называемому волновому уравнению, позволяющему определить V '
д2V ' |
a2 |
д2V ' |
0 |
, |
(4.18) |
|||
дt 2 |
|
дx2 |
|
|||||
0 |
|
|
|
|||||
где a0 
 kRT - адиабатическая скорость звука в среде;
kRT - адиабатическая скорость звука в среде;
по которому можно определить скорость распространения возмущений V .
Совершенно аналогичными по форме оказываются уравнения для и Р , которые можно получить из системы (4.17), если исключать из нее последовательно V или Р .
Отношения плотностей и давлений в среде при изменении скоростей воздуха в этом случае составляет
|
1 |
1 |
М |
2 |
... ; |
2(Р0 Р) |
1 |
1 |
M |
2 |
... ; |
(4.19) |
|
2 |
|
V 2 |
4 |
|
0
где М V / a - число Маха.
Расчеты по этим формулам показывают, что если V < 50 м/с, то относительная ошибка от неучета сжимаемости газа может составить 1%.
Ввысевающих системах скорость воздуха не превышает 20…30 м/с, так что ошибки от использования изобарной модели не могут превышать 1%.
Если свойства реальной среды заменить свойствами идеальной изобарной жидкости и пренебречь притоком тепла извне на участке присасывания семян, то уравнение (4.8) баланса энергии сплошной среды может быть сведено к уравнению, описывающему изменение кинетической энергии Т.
Вэтом случае движения воздуха по трубке тока вокруг семян (рис. 4.2) может быть описано уравнением Бернулли [4.12].
Рис. 4.2. Схема движения воздуха по трубке тока
V 2 |
P |
|
|
V 2 |
P |
|
|
|
|
||
1 |
|
1 |
g z |
|
2 |
|
2 |
g z |
|
. |
(4.20) |
|
|
|
|
2 |
|||||||
2 |
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Уравнение Бернулли позволяет определить давление воздуха в струях, обтекающих семена, если окажутся известными скорости элементов среды и геометрические параметры семян и аппарата, от которых зависят z1 и z2.

85
С помощью теоремы кинетической энергии (4.20) (теорема Бернулли) и теоремы количества движения (4.6) (теорема Эйлера) можно определить главный вектор сил давления среды на обтекаемый ею замкнутый контур.
Величина этого вектора, а вместе с тем и подъемной силы R (как ее называют в аэродинамике) определяется формулой Жуковского [4.12]:
R V Г , |
(4.21) |
где Г – циркуляция скорости потока V по контуру профиля С, определяемая контурным интегралом
Г V r ; |
(4.22) |
С |
|
V - скорость набегающего на контур потока жидкости.
Циркуляция потока зависит от вида потока, формы семян и конструкции пневматических каналов сеялки.
В общем виде потоки воздуха могут быть плоскими (что характерно, например, для щелевых пневматических аппаратов), осесимметричными или пространственными, а в зависимости от скорости воздуха и условий движения его в каналах потоки подразделяют на потенциальные (безвихревые) и вихревые.
Если движение среды безвихревое, то из условия равенства нулю вихря скорости rot V следует существование функции от координат и времени, связанной со скоростью V равенством
V grad |
, |
(4.23) |
или в проекциях на оси прямоугольных декартовых координат
v |
д |
; |
u |
д |
, |
(4.24) |
|
дх |
ду |
||||||
|
|
|
|
|
называемой потенциалом поля скоростей.
Уравнением поверхности уровня потенциала скоростей будет слу-
жить
(х, у, t) const .
Траектории движения частиц среды в случае стационарного потока (t= 0) совпадают с функцией тока
(х, |
у) С . |
(4.25) |
С помощью этой функции составляющие скорости u, v, также могут быть определены как частные производные:
u |
д |
; v |
д |
. |
(4.26) |
|
|
||||
|
дх |
|
дх |
|
|
Функция тока (х, у) и эквипотенциальные поверхности (х, у) (в случае плоского потока – кривые линии) образуют в совокупности гидродинамическую сетку, которая полностью определяет движение среды
(рис.4.3).
Если сопоставить равенства (4.24) и (4.26), то для соответствующих проекций скоростей потока можно получить равенства:

|
|
|
|
86 |
|
|
|
|
||
д |
|
д |
, |
д |
|
|
д |
, |
(4.27) |
|
дх |
ду |
ду |
дх |
|||||||
|
|
|
|
|
||||||
представляющие собой дифференциальные уравнения Коши-Римана, которым удовлетворяют вещественная и мнимая части всякой регулярной функции комплексного переменного f(z), где в данном случае z = x + iy.
(x, y, t) – const(x, y, t) – const
Рис. 4.3. Гидродинамическая сетка
Функцию i называют характеристической функцией плос-
кого потока или комплексным потенциалом функции f(z). Производная от характеристической функции
dx |
|
д |
i |
д |
u iv |
(4.28) |
|
dz |
дх |
дх |
|||||
|
|
|
|
представляет собой вектор, сопряженный с вектором скорости. Использование комплексного потенциала позволяет определять
компоненты скорости среды по одной переменной z, вместо двух – х и у.
В настоящее время в теории сплошной среды [4.1], [4.2], [4.3] определены значения , , для многих вариантов обтекания тел разнообразной формы как идеальной, так и вязкой жидкостью в потенциальных и вихревых потоках. Решены эти задачи для всех видов источников и стоков (линейных, плоских, осесимметричных, пространственных).
К сожалению, использование этих решений для анализа работы пневматического высевающего аппарата связано с определенными трудностями.
Дело в том, что определение потенциала и трубки тока связано с решением уравнения неразрывности потока (4.4)
ддхu ддуv 0 .
Подставляя в это уравнение вместо компонент скорости их выражения через потенциальную функцию по формулам (4.24) можно получить
д2 |
|
д2 |
0 , |
(4.29) |
|
дх2 |
ду2 |
||||
|
|
|
уравнение Лапласа, которое, как уравнение в частных производных, имеет бесчисленное множество решений.
Дополнительными требованиями, позволяющими определить функцию в конкретных случаях, являются граничные условия.
При решении задачи обтекания тела используют [4.5], [4.10], [4.11] два граничных условия:
87
[V ] |
|
|
|
д |
0 и V |
V . |
(4.30) |
|
s |
|
|
|
|||||
n |
|
|
|
|
|
|||
|
|
|
|
дn s |
|
|
|
|
Первое из условий является выражением непроницаемости тела, т.е. нормальные составляющие скорости воздуха на его поверхности должны быть равны 0.
По второму условию на весьма далеком расстоянии от тела, где возмущающее влияние тела на поток отсутствует (условно говоря на бесконечности), поток должен иметь заданную скорость V .
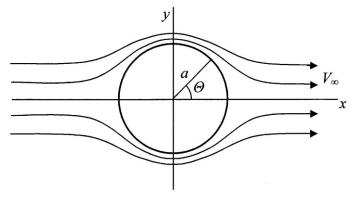
Например, при обтекании сферы плоским потоком (рис.4.4) распределение скоростей на ее поверхности может быть описано уравнением
|
|
|
|
|
1 |
|
|
|
|
3 |
|
|
|
Vz |
|
отн |
|
|
|
|
отн |
|
|
|
V sin |
. |
(4.20) |
S |
|
|
|
||||||||||
|
r a |
r |
r a |
|
2 |
|
|
|
|||||
Рис. 4.4. Схема движения воздуха около сферы
Аналогично может быть определено распределение скоростей воздуха при обтекании цилиндра (рис 4.5а) и эллипса (рис. 4.5б).
Для случая цилиндрического тела
Vr a 2V sin , |
(4.32) |
|||
а для эллипсоида |
|
|
|
|
V (1 |
b |
)V |
cos . |
(4.33) |
|
||||
r |
a |
|
|
|
|
|
|
|
|
При выводе уравнений (4.31), (4.32), (4.33) предполагалось, что в зоне движения воздуха около тела нет источника или стока, т.е. V = V∞.
В действительности семена присасываются к отверстию высевающего диска, т.е. именно к стоку, который расположен в непосредственной близости от семян.
Характеристики источников и стоков представлены на рис. 4.6 и 4.7
и соотношениях (4.34) и (4.35) [4.12].
Так, для источника (стока), расположенного в начале координат, с секундным объемным расходом Q – действительной положительной величиной в случае источника и отрицательно в случае стока
(z) Q ln z ; Q ln r ; |
Q ; |
V Q |
; |
V |
Q |
; (4.34) |
|||||||||
|
|
|
|
|
|
|
|
_ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
2 |
|
2 z |
|
|
2 r |
|||||
где r, ε - полярные коэффициенты.

88
а |
б |
Рис. 4.5. Схема движения воздуха около тела в виде цилиндра (а) и эллипса (б)
а) источник б) сток Рис.4.6. Потоки воздуха в источнике и стоке
В случае вихревого движения, изолированного в начале координат (рис.4.7), с циркуляцией Г характеристики стока могут быть представлены
[4.5], [4.12] как
|
( z) |
|
Г |
ln Z ; |
|
Г |
; |
|
Г |
ln r ; |
V |
Г |
; |
|
V |
|
|
|
|
Г |
|
|
. |
(4.35) |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
2 |
|
|
2 |
|
2 |
|
2 Z |
|
|
|
|
|
2 r |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Движение воздуха, в случае близкого расположения характерных элементов воздуховодов, может быть описано путем использования конформных преобразований [4.1], [4.2], [4.3], или методом наложения потоков.
Метод наложения для потенциальных потоков может быть реализован с учетом того, что потенциал суммарного поля скоростей может быть представлен в виде суммы потенциалов отдельных составляющих
1 2 ... n . |
(4.36) |
Рис.4.7. Движение воздуха в вихре
89
Результирующая скорость может быть найдена как
_ |
_ |
_ |
_ |
|
V рез V 1 |
V 2 |
...V n . |
(4.37) |
|
Например, суммирование потенциалов вихря и стока описывает движение среды в так называемом вихрестоке (рис.4.8) [4.5].
(z) |
Q Гi |
ln z |
(4.38) |
|
|||
|
2 |
|
|
Рис. 4.8. Движение воздуха в вихрестоке
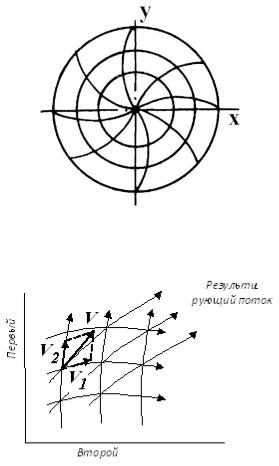
В случае потенциальных и вихревых потоков может быть использован графический способ построения линий тока результирующего потока
(рис. 4.9).
Рис. 4.9. Схема определения результирующей скорости
Данный способ легко с достаточной точностью может быть реализован на ЭВМ.
4.2Модель процесса захвата семян аппаратами магнитных
иэлектромагнитных сеялок
Движение электрически заряженных или магнитных частиц в электромагнитном поле зависит от напряженностей Е электрического и Н магнитного полей [4.15], [4.16]. Эти напряженности в каждой конкретной точке определяют по силе, действующей на пробный заряд, помещенный в эту точку
F e(E |
V |
H ) , |
(4.39) |
|
c |
||||
|
|
|
где e – пробный заряд; V – скорость движения заряда; с – константа с размерностью, равной скорости света в пустоте.

90
Если рассматривать движение не одной, а нескольких (системы) заряженных частиц сплошной среды, то
|
|
1 |
|
|
|
|
F e E |
|
e Va H |
, |
(4.40) |
||
c |
||||||
|
|
|
|
|
||
где Va – скорость одной из частиц а.
Суммирование производится по всем частицам внутри элементарного объема Δη.
Величины |
|
|
е |
и |
j |
e Va |
называют, соответственно |
|||
е |
t |
|
|
|
||||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
плотностью заряда и плотностью тока. |
|
|
||||||||
Соответственно этому плотность силы f = F / Δη примет вид |
||||||||||
|
|
|
f |
E |
1 |
( j H ) . |
(4.41) |
|||
|
|
|
|
|||||||
|
|
|
|
e |
|
c |
|
|
||
|
|
|
|
|
|
|
|
|||
В изменяющихся во времени электрических и магнитных полях их напряженности оказываются взаимозависимыми [4.15], в соответствии с уравнениями Максвелла, записанными в интегральной форме:
H
L
E
L
|
4 |
|
|
1 |
|
E |
|
|
|
||||
d |
|
|
|
|
I |
|
|
|
n d |
|
|||
|
c |
c |
|
|
|||||||||
|
|
|
|
|
t |
|
(4.42) |
||||||
|
|
1 |
|
|
H |
|
|
|
|
, |
|||
d |
|
|
d |
|
|
|
|||||||
|
|
|
|
|
|
|
|||||||
|
c |
t |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||
где I - ток протекающий через поверхность .
В дифференциальной форме уравнения Максвелла представляется в
виде:
rotH
rotE
4 |
j |
|
1 F |
|
||||
|
|
|
|
|
|
|||
|
|
c t |
|
|||||
c |
|
|
|
(4.43) |
||||
|
|
|
. |
|||||
|
1 H |
|
|
|||||
c |
|
t |
|
|
||||
|
|
|
|
|||||
К уравнениям Максвелла относят обычно еще принцип непрерывности магнитных силовых линий, так что их поток через замкнутую поверхность равен нулю
Hd 0 |
|
(4.44) |
|
|
|
и обобщенную теорему Гаусса |
|
|
End 4 Q |
, |
(4.45) |
|
|
|
где Q ed - заряд, заключенный внутри σ.
В дифференциальной форме два последних соотношения образуют систему
divH 0
. |
(4.46) |
divE 4 e |
|
