862

92

eV – конвективные токи, возникающие в частично ионизированном газе. После ряда некоторых упрощений в этом случае можно получить си-

стему уравнений магнитной гидродинамики

О схожести уравнений гидродинамики и электрогидродинамики говорят даже сравнительно общие характеристики среды.

Если в механике вязкой жидкости используется понятие кинематической вязкости, то в электрогидродинамике используют аналогичную ей

магнитную вязкость [4.18].

Аналогично числу Рейнольдса движущего потока введено понятие

магнитного числа Рейнольдcа.

Если, например, Rm > 1, то в уравнениях движения можно пренебречь электрической силой по сравнению с магнитной.

4.3 Модель процесса пневмотранспортирования семян

Подавляющее большинство пунктирных сеялок не имеют семяпровода. Как правило, семена из выгрузного окна падают в сошник, а точнее в борозду, образованную внутри сошника.

Негативное влияние семяпровода на равномерность распределения уже давно было выявлено В.Е. Комаристовым и затем многими другими исследователями.

Но устранение семяпровода вызвало целый ряд конструкторских затруднений. Это связано с ограничениями минимальной величины междурядья, невозможностью организации централизованного высева семян, необходимостью изыскания способов уменьшения раскатывания семян в бороздке, так как существует значительная разница между скоростью движения сеялки по полю и скоростью выхода семян из аппарата.

93

Кроме того, в последние годы начали проводиться работы по использованию принципов пневмоники, когда семена из псевдоожиженного состояния в бункере импульсным воздушным потоком транспортируются к борозде.

Преимуществами таких аппаратов является универсальность, отсутствие на сеялке (посевной секции) вращающихся частей (цепей, звездочек, дисков), использование пневмоавтоматики для целей регулирования процесса и контроля за качеством высева.

Немаловажным является опыт решения аналогичных задач в теории контейнерного трубопроводного транспорта, в частности, организации пневмопочты с очень сложными системами трубопроводов, соответствующих произвольному профилю трассы, путевыми сбросами, эжекторами, байпасными устройствами при высокой плотности элементов [4.13], [4.14].

Процесс пневмотранспортирования семян может быть использован для обеспечения заданной скорости их падения в бороздку, образованную сошником. Если скорость семян, покидающих семяпровод, по величине будет равна скорости движения агрегата, а направлена в противоположную сторону, то раскатывания их в бороздке не произойдет, либо окажется минимальным.

Устройство, обеспечивающее выброс семян из пневмопровода с заданной скоростью и снижение отрицательного воздействия воздуха в посевной борозде изучено в Воронежском ГАУ [4.19] сотрудниками кафедры сельскохозяйственных машин А.П. Тарасенко, В.В. Василенко, В.А. Гребцовым и др.

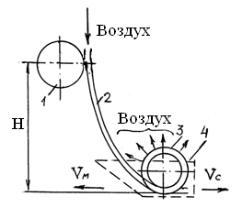
Устройство представляет собой семяпровод в виде полиэтиленовой трубки определенной формы и размеров (рис. 4.10), к нижней части которого закреплено выбросное устройство в виде изогнутой по спирали трубки (один виток) с отверстиями по наружной стенке для выхода воздуха.

Рис.4.10 Схема высева с пневмотранспортированием семян:

1 – высевающий аппарат; 2 – семяпровод; 3 – выбросное устройство; 4– сошник

Скорость семян на выходе семяпровода регулируется за счет изменения проходного сечения отверстий, размещенных в стенках выбросного устройства, с помощью специальной заслонки.

При высеве семян кукурузы оптимальными оказались семяпроводы с внутренним диаметром 20 мм, выполненными по эллиптической или параболической кривой.

Диаметр витка выбросного устройства в этом случае должен равняться 200 мм. Коэффициент живого сечения радиальных отверстий необ-

94

ходимо изменять в пределах 0,06…0,25. Оптимальной скоростью воздушного потока оказались величины 28…32 м/с.

Скорость выброса семян кукурузы в этом устройстве может регулироваться в пределах 1,6…3,5 м/с.

При изучении влияния пневмотранспортирования на равномерность высева и повреждения семян установлено, что после пролета по семяпроводу показатели качества выходного потока снижаются по сравнению с исходным.

Большее нарушение равномерности исходного потока характерно для малой нормы высева. Коэффициент вариации интервалов времени вылета отдельных семян увеличивается на 3…11%. Дробление семян не превышает

0,3%.

Дисперсионный анализ технологического процесса показал, что при равенстве скорости выброса семян с рабочей скоростью посевного агрегата относительное влияние пневмосемяпровода на точность распределения семян составляет около 60%, относительное влияние перекатывания семян по дну борозды не превышает 10%.

Увеличение длины семяпровода снижает равномерность распределения семян и при длине трубок, равных 0,74 м, высев находится уже на уровне серийных пунктирных сеялок (σс = 10…13 см).

В работе [4.19] проведены и теоретические исследования, направленные на определение скорости семян, находящихся под воздействием воздушного потока, на различных участках семяпровода. Составлены дифференциальные уравнения, определяющие движение семян, как по основной части семяпровода, так и по кольцу выбросного устройства.

К сожалению, решение выполнено при весьма существенных допущениях, таких как движение одной материальной точки с постоянным скольжением по внешней стенке семяпровода, постоянной площади миделева сечения частиц, плотности воздуха и направления вектора скорости воздуха только вдоль оси пневмопровода.

При достаточно большой длине трубопровода в нем может располагаться несколько одновременно движущихся семян различных размеров.

Параметры воздушного потока (направление и величина скорости воздуха, давление, температура), безусловно, будут зависеть от числа движущихся семян, величины зазоров между ними и семяпроводом (о которых зависят перетоки газа).

Уравнение, предложенное автором в работе [4.19], не учитывают ряда существенных факторов. В них не учитывается величина напора воздуха (давления) ни в начальной точке, ни в любом из последующих положений. В уравнения не входят даже такой существенный параметр, как внутренний диаметр трубопровода.

Более полное описание движения системы частиц под действием потока газа по трубопроводу произвольной формы возможно при использовании методов механики сплошной среды, транспонированных к условиям движения семян по семяпроводу.

95

4.3.1 Основные уравнения одномерного течения воздуха в семяпроводе (трубе)

Как и в случае изучения течения воздуха около семян, в основе описания движения воздуха в семяпроводе могут быть использованы уравнения механики сплошной среды [4.13], выражающие законы сохранения массы газа (4.3) приводящей к уравнению неразрывности потока (4.4), количества движения (4.5), изменения количества движения (4.6) и энергии

(4.8).

В интегральной форме применительно к движению по трубе эти

где η(dη) –произвольный объем сплошной среды, состоящий из одних и тех же частиц: А(dζ)- поверхность, ограничивающая этот объем, ρ - плотность газа, V - скорость газа, Рn – вектор напряжений на площадке с нормалью n, F – плотность массовых сил , U – внутренняя энергия единицы объема газа, qn –нормальная составляющая вектора потока тепла.

Преобразуя поверхностные интегралы в формулах (4.52), (4.54) в интегралы по объему η с помощью формулы Гаусса–Остроградского, можно получить:

где Р - тензор напряжений в газовой среде;

Р = -РI + T (здесь Р – давление газа; I – единичный тензор; Т – тензор касательных напряжений).

Используя известную формулу дифференцирования по времени интеграла с переменными пределами интегрирования

можно уравнения (4.52), (4.55), (4.56) привести к виду:

( div V )d 0;

t

98

Согласно формуле Н.Е. Жуковского, колебания давления δρ можно

оценить равенством

с Q ,

а колебания величины βρV2 равенством

( V 2 ) V Q ,

где δQ – колебания расхода газа.

Отношение колебаний рассмотренных величин, составляет

( V 2 ) V ,C

причем, числитель дроби мал по сравнению с ее знаменателем.

3.Тепловой поток вдоль оси трубы мал по сравнению с потоком тепла в перпендикулярном направлении и его можно не учитывать.

4.Рассматриваемый газ в условиях низконапорных пневматических систем можно считать совершенным, для которого уравнения состояния имеет вид:

P RTг ;

а выражения для термодинамических функций запишутся так:

где R - газовая постоянная; CV, Cp – удельные теплоемкости изохорного и изобарного процессов; Тг - температура газа.

С учетом сделанных допущений систему уравнений (4.61) и добавочные условия для U и P можно представить в виде

При выводе этих уравнений принято, что проекция массовых сил, действующих на газ, равна нулю. Система уравнений (4.64) является уже замкнутой, т.е. позволяет определить шесть неизвестных величин

, Р,V,Q,Тг ,U .

Третье уравнение системы (уравнение притока тепла) можно упростить, если прибавить к нему почленно второе уравнение (уравнение движения), умноженное предварительно на скорость газа V.

Допущение о малости числа Маха приводит к уравнению

100

Выражение RTв представляет собой адиабатическую скорость

звука в газе:

C 2 ( dPd )s RTb ,

где производную определяют при постоянной энтропии S.

Система уравнений (4.65) для рассматриваемого случая примет вид:

Так как изменения температуры газа малы, то скорость звука в нем можно считать постоянной.

Система уравнений (4.67) относительно двух функций – давления P(x,t) и расхода Q(x,t) – может быть использована в качестве исходной для расчета движения газа по трубам в изотермических условиях.

4.3.2 Математическая модель движения семян по семяпроводу

Пусть семяпровод представляет собой трубку малого диаметра с произвольным профилем, движение газа в котором (при отсутствии семян) описывается системой уравнений (4.67).

Рассмотрим участок семяпровода, расположенного между сечениями х=0 и х=L, где L – длина участка, отсчитываемого вдоль оси трубки х.

Пусть в некоторый момент времени на этом участке находится одно или несколько семян. Движение каждого семени описывается неизвестной и подлежащей определению функцией x j (t) (здесь j=1,2…N), которую

будем называть траекторией j-го семени.

Траектории семян разбивают рассматриваемый участок семяпровода на несколько областей, в каждой из которых движется только газ, а семена представляют собой границы этих областей. Для нахождения этих границ можно использовать обыкновенные дифференциальные уравнения, выражающие второй закон Ньютона:

ление газа за и перед семенем; g - ускорение свободного падения; α(х) - угол наклона оси семяпровода к горизонтали в той точке трассы x j (t) ,

в которой находится j-е семя в данный момент времени; Fcj - сила сопротивления, вызванная трением.

Уравнения (4.68) и (4.69) незамкнуты, и их нельзя решить отдельно, так как в каждое из них входят неизвестные P ( j ) и P ( j ) , значения которых определяются в процессе решения газодинамических уравнений.