2.5.6. Статистическая модель многокритериального принятия решений на основе принципов оптимальности в условиях неопределенности

Модель многокритериального принятия ре­шений при риске представлена в разделе 2.3. Как и в однокритериальном случае, при оценивании качества альтерна­тив возможна одна из следующих трех ситуаций априорной информирован­ности ЛПР о состояниях среды (раздел 2.5.1).

Ранее уже рассмотрена проблема выбора альтернативы по одному локаль­ному критерию (характеристике) качества в зависимости от поведения среды, описаны критерии оценки и выбора, по которым сравнивают альтернативы. Данные критерии назывались также критериями снятия неопределенности.

После того как удается оценить каждый локальный критерий (характе­ристику) качества, избавившись от случайности или риска выбора, задача становится детерминированной и для ее решения можно применить методы многокритериального принятия решений при определенности.

Предлагаемый подход можно рассматривать как двухуровневое решение задачи выбора. На нижнем уровне рассматривается решение задачи оцени­вания вариантов решений каждого из локальных критериев (харак­теристик) качества , вводя или конструируя специальные критерии снятия неопределенности и избавляясь формально от случайных составляю­щих, связанных с поведением среды. Выбор специальных критериев снятия неопределенности зависит от априорной информированности ЛПР.

Задача принятия решений состоит в выборе ЛПР наилучшего варианта (строки матриц при представлении функции полезности или потерь в виде матриц), имеющего наибольшую полезность или наименьшие потери , в зависимости от смысла оценок локальных критериев или характеристик каче­ства

2.5. Методы оптимизации

Для решения задачи снижения рисков информационной безопасности необходимо предложить и реализовать комплекс мер контроля и управления (защитных мер). Таким образом, под системой информационной безопасности будем понимать совокуп­ность отдельных элементов (мер контроля и управления), взаимодействующих в процессе функционирования системы, выполняющих определенную задачу. При разработке или совер­шенствовании системы информационной безопасности естественно стремление сделать ее наилучшей в каком-либо смысле. Под этим понимается синтез такой системы информационной безопасности, в процессе функционирования которой обеспечивалось бы экстремальное значение не­которого критерия — показателя качества или эффективности работы. Качество функционирования системы характеризуется не­которым числовым показателем — целевой функцией, которую требуется обратить в результате оптимизации в экстремум. Далее для определенности будет рассматриваться задача минимизации (например, минимизация риска, минимизация стоимости реализации системы).

Случаи, когда имеется несколько целевых функций или целевая функ­ция не является числовой, рассматривались ранее в разделах 2.3-2.5.

Минимизация целевой функции должна быть выполнена при соблюде­нии определенных ограничений. Ограничения могут быть весьма разнооб­разными и определяются многими факторами, например, условиями физи­ческой реализуемости при проектировании системы, условиями эксплуата­ции, гарантирующими надежную работу объекта, техническими заданиями на характеристики объекта.

Методы решения задач оптимизации условно разделяются на два класса: аналитические и поисковые. Применение аналитических методов связано с условиями экстремума. Данными методами решаются задачи вариационно­го исчисления и задачи оптимального управления. Однако найти с помо­щью условий экстремума явное решение задачи удается в редких случаях.

Среди множества задач оптимизации выделим конечномерные задачи статической оптимизации, т.е. задачи, в которых значения целевой функ­ции не зависят от времени. К ним сводятся задачи оценки параметров при обработке статистических данных, задачи решения систем алгебраических уравнении, систем дифференциальных уравнений, задачи экспериментальной оптими­зации, поиска экстремума сложных функций при проектировании системы и т.д.

Постановка любой задачи оптимизации начинается с определения набора независимых переменных, выделения зависящей от них функции качества (риска) и определения условий (ограничений), которые характеризуют приемлемые или допустимые значения независимых переменных. Рассмотрим случай, ко­гда функция качества (риска) является скалярной функцией, называемой целевой функцией. Решение задачи оптимизации состоит в определении допустимых значений переменных, которым соответствуют оптимальные значения целе­вой функции. Под оптимальностью будем понимать минимальность.

Рассмотрим численные методы решения конечномерных статических за­дач условной оптимизации, называемых также задачами нелинейного матема­тического программирования (ЗНП), постановка которых сводится к виду

найти

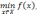
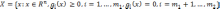
где целевая функция и функции ограничений — вещественные скаляр­ные функции.

Как следует из постановки задачи, ее особенности связаны с видом целе­вой функции и ограничений. Приведем наиболее распространенные виды целевой функции : 1) функция одной переменной: 2) функция многих пе­ременных; 3) линейная функция; 4) квадратичная функция; 5) гладкая не­линейная функция; 6) выпуклая гладкая функция; 7) выпуклая функция; 8) негладкая нелинейная функция; 9) стохастическая функция; 10) непре­рывная функция; 11) разрывная функция; 12) нечеткая функция.

Виды ограничений : 1) ограничения отсутствуют; 2) простые ограниче­ния; 3) линейная функция; 4) квадратичная функция; 5) выпуклая гладкая функция; 6) гладкая нелинейная функция; 7) выпуклая функция; 8) неглад­кая нелинейная функция; 9) непрерывная функция; 10) стохастическая функция; 11) нечеткая функция.

Сочетание конкретных видов целевых функций и ограничений порожда­ет определенные классы задач оптимизации:

• при отсутствии ограничений — задачу безусловной оптимизации;

• при линейных ограничениях и целевой функции — задачу линейного программирования;

• при линейных ограничениях и квадратичной целевой функции — зада­чу квадратичного программирования;

• при выпуклости множества X и функции f(x) — задачу выпуклого про­граммирования,

• при негладкой целевой функции — задачу недифференцируемой опти­мизации;

• при нескольких целевых функциях — многокритериальную задачу оп­тимизации;

• при стохастических ограничениях или целевой функции — задачу сто­хастического программировании;

• при нечетких ограничениях или целевой функции — задачу нечеткого математического программирования или нечеткой оптимизации.

Важным признаком задачи оптимизации является ее размерность, от ко­торой зависят объем памяти и количество вычислений, необходимых для решения задачи. Под размерностью задачи будем понимать количество не­зависимых переменных n и число ограничений m.

Другой признак, от которого зависит выбор метода решения, – вид доступ­ной информации. Будем придерживаться следующей классификации мето­дов. Методы прямого поиска, или нулевого порядка, используют информацию только о значениях целевой функции. Методы первого порядка используют значения целевой функции и ее первых производных, методы второго поряд­ка — значения целевой функции, первых и вторых производных.

Доступность производных связывается с построением процедуры расче­та точных значений производных, приемлемой точностью вычисления про­изводных (при использовании конечно-разностных представлений) и тру­доемкостью процедуры. Эти затраты должны сопоставляться с общими затратами на решение задачи оптимизации.

В итеративных процедурах методов первого и второго порядка использу­ется информация, по крайней мере, о градиентах функций, входящих в фор­мулировку задачи (в первую очередь знание градиента целевой функции). К методам этого класса, прежде всего, относятся градиентные методы (и их модификации), метод Ньютона (и его модификации), квазиньютоновские методы, методы переменной метрики, метод сопряженных направлений. Методы данного класса довольно подробно описаны в литературе, посвя­щенной теории оптимизации.

Методы прямого поиска основаны на использовании значений оптими­зируемой целевой функции. Их стратегия заключается в использовании значений функции для конечно-разностной аппроксимации градиента функции, матрицы вторых производных. К этим методам относятся метод покоординатного спуска, методы случайного поиска, метод сопряженных направлений, метод Хука-Дживса и класс методов деформируемых конфи­гураций.

Теоретически наиболее сильные результаты в теории оптимизации полу­чены для методов второго и первого порядка. Для большинства этих мето­дов проведено достаточно полное аналитическое исследование свойств ме­тодов, доказана сходимость методов, получены оценки скорости сходимо­сти. Методы прямого поиска менее исследованы, многие из них носят эври­стический характер. Если сравнивать методы двух классов по скорости схо­димости, то преимущество получат методы первого класса.

Подчеркнем, что не существует универсального метода оптимизации, применение которого оправдано и эффективно во всех случаях. Выбор того или иного метода должен быть согласован с конкретными условиями и огра­ничениями, вытекающими из специфики решаемой задачи оптимизации, доступной информации.

Сделаем терминологическое замечание. Под «методом» понимаем общее описание действий по решению соответствующей задачи, отражающее структуру действий без детализации; под «алгоритмом» — более частное, де­тализированное описание метода, частный вариант метода.

Постановки задач поисковой оптимизации отличаются большим разно­образием. В ряде случаев имеется возможность достаточно частых и даже непрерывных измерений значений оптимизируемой функции. В других си­туациях временные и экспериментальные затраты на измерения столь зна­чительны, что приходится ограничиваться небольшим их числом. Естест­венно, что в таких задачах предпочтение должно быть отдано дискретным методам, обеспечивающим приемлемое решение за малое число итераций.

Приведем основные формальные постановки задач, к которым могут быть сведены задачи выбора оптимального комплекса мер контроля и управления, и решению которых посвящены различные методы оптимизации.

Пусть действительная скалярная функция определена на множест­ве X -мерного евклидова пространства (варианты множества X описаны ниже). Пусть в точке (предполагается, что такая точка существует) функ­ция достигает минимального значения на множестве , т.е.

Требуется построить оценку точки (с некоторой точностью, на­пример, чтобы или , где – заданная точ­ность) на основе конечного числа измерений значений функции либо на основе конечного числа итераций, где число измерений функции на каждой итерации ограничено.

Необходимо отметить, что при описании задач оптимизации использу­ются операторы min и max, применение которых корректно лишь в тех слу­чаях, когда достигается нижняя или верхняя грань (минимум или макси­мум) оптимизируемой функции. При невыполнении условия достижимо­сти грани для корректности описания задач операторы min и max должны заменяться на операторы inf (от «infinum» - точная нижняя граница) и sup (от «suprenum» - точная верхняя граница). Далее будем подразумевать, где это необ­ходимо, что операторы min и max читаются как inf и sup.

Множество значений переменной ограничено множеством допустимых значений , которое образовано ограничениями. Рассмотрим методы решения задач следующих типов:

• задачи безусловной минимизации, когда множество допустимых значе­ний X совпадает с пространством ;

• задача минимизации с простыми (интервальными) ограничениями, ког­да множество имеет вид

где – -я независимая переменная; 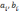– константы, определяющие ниж­нюю и верхнюю границы изменения ;

• задача минимизации с линейными ограничениями, когда множество X имеет вид

• задачи минимизации с ограничениями типа равенств и неравенств:

.

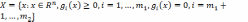
При решении практических задач распространенной является ситуация, когда информация о значениях оптимизируемой функции и об ограничениях искажена ошибками различного типа. В этом случае доступна информация о поведении оптимизируемой функции в виде y(x)=f(x)+ , где – ошибка, имеющая случайную или детерминированную природу.

Подробно вопросы оптимизации рассмотрены в работах [1, 5, 32-38, 68].