2.5.2.3. Критерий максимизации вероятности распределения функции полезности

Выберем величину , удовлетворяющую неравенствам , где ; .

Каждое решение оценивается критерием 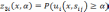– вероятностью того, что значение функции полезности не меньше для состояния среды . Смысл критерия максимизации вероятности распределения функции полезности заключается в нахождении решения , для которого

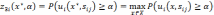
При использовании этого критерия ЛПР исходит из задания конкретного значения и оптимальными считает те решения , для которых выполнено это условие.

Если используется функция потерь , то для каждого решения определяется вероятность и применение критерия состоит в выборе решения , для которого

где значение выбирается ЛПР из отрезка .

2.5.2.4. Модальный критерий

Модальный критерий конструируется исходя из наиболее вероятного состояния среды.

Предположим, что существует единственное значение В этом случае ЛПР полагает, что среда находится в состоянии и оптимальное решение определяется из условия

Если же окажется, что максимум достигается на априорных вероятностях , то оптимальное решение определяется из условия

Основным недостатком рассматриваемого критерия является возможность того, что если взять два решения и , для которых , то по модальному критерию предпочтительным будет решение , т.е. Однако при этом может оказаться, что .

К преимуществам модального критерия можно отнести:

• использование наиболее вероятных состояний среды; при этом совсем не обязательно знать количественные значения самих вероятностей осуществления этих состояний;

• возможность определения функции полезности лишь для наиболее вероятных состояний среды, что во много раз увеличивает скорость принятия решения.

Отметим, что при использовании функции потерь операция max заменяется на min.

2.5.2.5. Критерий минимума энтропии математического ожидания функции полезности

Прежде чем описывать критерий, дадим краткое описание энтропии. Энтропия может служить мерой оценки неопределенности. Пусть с вероятностью тогда мерой неопределенности является энтропия:

Энтропия – неотрицательная величина. Если одно из равно единице, то — ситуация отсутствия неопределенности. При , , величина энтропии максимальна ( ) — ситуация полной неопределенности.

Перейдем к описанию критерия. Предположим, что для всех и Энтропию математического ожидания функции полезности для решения определим следующим образом:

Здесь в качестве вероятностей выступают взвешенные нормализованные величины

Требуется найти решение (либо X^*) из условия

В случае невыполнения условия для всех и выполняется переход от значений функции полезности к риску (сожалениям, потерям) вида

В этом случае решение находится из условия минимума по энтропии математического ожидания функции полезности вида при :

2.5.2.6. Критерий Гермейера

Рассмотрим критерий Гермейера, ориентированный на величины потерь, которые описываются функцией с отрицательными значениями , .

Согласно критерию Гермейера оптимальными решениями считают такие решения, для которых

Во многих прикладных задачах приходится иметь дело с ценами и затратами и условие выполняется. В случае, когда среди величин встречаются и положительные значения, можно перейти к строго отрицательным значениям с помощью преобразования при . Отметим, что в этом случае решение зависит от b.

Правило выбора по критерию Гермейера формулируется следующим образом.

Функция потерь дополняется столбцом, содержащим в ка­ждой строке наименьшее произведение имеющегося в ней результата на ве­роятность соответствующего состояния , т. е. каждое решение оценивает­ся взвешенной величиной. Выбираются те варианты , в строках которых находится наибольшее значение этого столбца.

Отметим, что если вероятности состояний среды точно не известны, а число использований матрицы решений мало, то, следуя критерию Гермейера, получают неоправданно большой риск.