2.6. Интегрирование иррациональных и трансцендентных функций
Предварительно
введем обозначение рациональной функции
от двух переменных u
и v,
т. е. функции, получающейся из двух
переменных u
и v
и некоторых
постоянных, над которыми производятся
только операции сло-жения, вычитания,
умножения и деления: 
.
Такова, например, функция
Если переменные
u
и v,
в свою очередь, являются функциями
переменной х:
то функция
называется рациональной функцией от
и
Например, функция
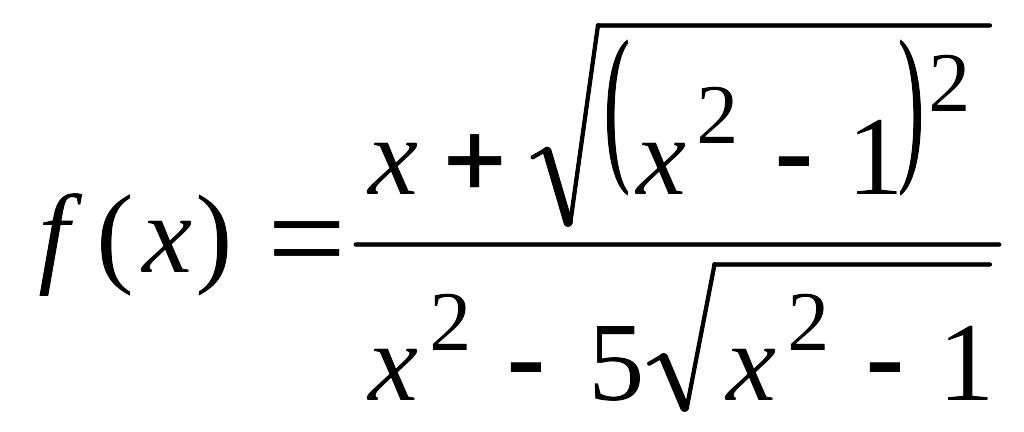
является рациональной
функцией от х
и от
здесь
,
а функция
является рациональной функцией от
и от
:
Рассмотрим теперь интегралы от некоторых простейших иррациональных и трансцендентных функций и покажем, что в ряде случаев они сводятся к интегралам от рациональных функций (или, как говорят, рационализируются) и могут быть вычислены методами, рассмотренными в п. 2.5.
1. Интеграл вида
где a,
b,
c,
d,
некоторые числа
m
–
натуральное число, R
– рациональная функция от х
и от
Покажем, что такой
интеграл рационализируется подстановкой
В самом деле,
так что
где
рациональная
функция аргумента t.
Пример 1.
Вычислить
Решение.
Сделав
подстановку
получим
Далее, имеем
Пример
2.
Вычислить
Решение. Имеем
2. Интеграл вида
где a,
b,
c
– некоторые числа;
R
– рациональная функция от х
и от
Если трехчлен
имеет действительные корни
и
,
то
.
Следовательно,
т.
е. получаем интеграл, рассмотренный в
п. 1.
Если
то
т.е. под знаком интеграла находится
рациональная функция от х.
Поэтому интересен
случай, когда трехчлен
не имеет действительных корней и
.
Покажем, что в данном случае интеграл
рационализируется подстановкой Эйлера
Возводя обе части
равенства
в квадрат, получаем
так что
Таким образом,
где
рациональная функция от t.
Если же в трехчлене
а
то для рационализации интеграла можно
применить другую подстановку Эйлера
Пример 3.
Вычислить
.
Решение.
Поскольку трехчлен
имеет комплексные корни, сделаем
подстановку
Возводя обе части равенства в квадрат,
получаем
или
отсюда
Тогда
Далее имеем
Умножая обе части
равенства на
получаем
или
Приравнивая коэффициенты при одинаковых степенях t, относительно A, B, и D получаем систему уравнений
первой
степени
откуда A = 2, B = 3, D = 3. Следовательно,
и окончательно
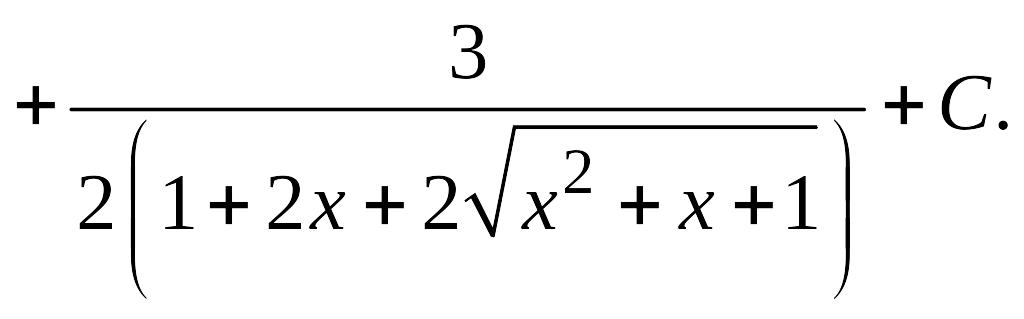
Пример 4.
Вычислить
Решение.
Здесь в трехчлене
,
,
поэтому воспользуемся подстановкой
Возводя обе части равенства в квадрат,
получаем
или
отсюда
Таким образом,
Заметим, что вычисление интегралов с помощью подстановок Эйлера обычно приводит к громоздким выражениям и трудоемким выкладкам, поэтому их следует применять, только если данный интеграл не удается вычислить более коротким способом.
3. Интеграл вида
где R
рациональная функция от sin
x и от cos
x. Покажем,
что интеграл рационализируется
подстановкой
Действительно,
так что
где рациональная функция от t.
Пример 5.
Вычислить
Решение.
Применяя подстановку
получаем
Таким образом,
4. Интеграл вида
Покажем, что данный интеграл
рационализируется подстановкой
В самом деле, так как
то
где
рациональная функция от t.
Пример 6.
Вычислить
Решение.
Полагаем
,
отсюда
Следовательно,
В заключение отметим, что рассмотренные методы и приемы интегрирования не исчерпывают всех классов аналитически интегрируемых элементарных функций. В то же время из всего изложенного следует, что операция интегрирования сложнее операции дифференцирования. Необходимы определенные навыки и изобретательность, которые приобретаются на практике в результате решения большого числа примеров.
Отметим также, что если дифференцирование не выводит из класса элементарных функций, то при интегрировании дело обстоит иначе. Существуют такие элементарные функции, первообразные от которых не являются элементарными функциями. Такие первообразные не только существуют, но и играют большую роль как в самом математическом анализе, так и в его приложениях. Они хорошо изучены, для них составлены таблицы и графики, помогающие их практическому использованию.
Если первообразная не является элементарной функцией, то говорят, что интеграл «не берется» в элементарных функциях.