4.5. Степенные ряды

1. Определение и общие замечания. Ряд вида

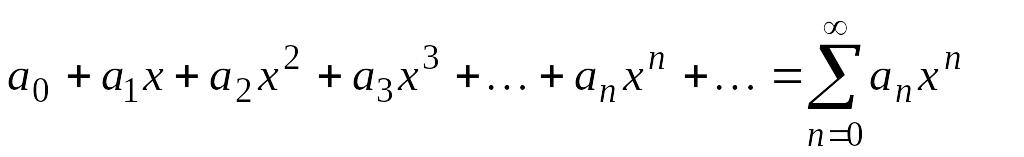(4.9)

называется степенным рядом.

Числа называются коэффици-ентами степенного ряда.

Придавая х различные числовые значения, будем получать раз­личные числовые ряды, которые могут оказаться сходящимися или расходящимися. Множество тех значений х, при которых ряд (4.9) сходится, называется областью его сходимости. Это множество всегда не пусто, так как любой степенной ряд сходится при Очевидно, что частичная сумма степенного ряда является функцией переменной х. Поэтому и сумма ряда S также является некоторой функцией переменной х, определенной в области сходимости ряда:

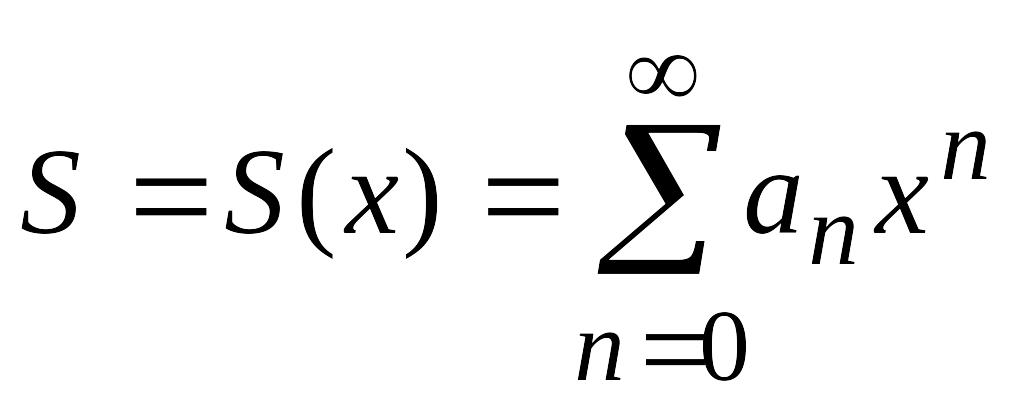
2. Интервал сходимости степенного ряда. Сформулируем теорему, имеющую важное значение в теории степенных рядов и касающуюся области сходимости степенного ряда.

Теорема 12 (теорема Абеля). 1) Если степен­ной ряд (4.9) сходится при , то он сходится, и при­том абсолютно, для всех х, удовлетворяющих условию

2) если ряд (4.9) расходится при , то он расходится для всех х, удовлетворяющих условию .

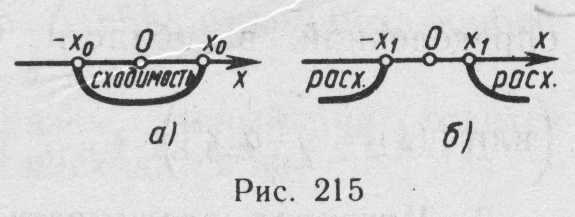Т еорема Абеля утверждает, что если точка сходимости степенного ряда, то во всех точках, расположенных на интервале (рис. 20, а), этот ряд сходится абсолютно, а если  точка расходимости степенного ряда, то во всех т

Рис. 20

очках, рас­положенных вне интервала (рис. 20,б), ряд рас­ходится. Отсюда вытекает следующая теорема.

Т

Рис. 20

еорема 13. Если ряд сходится не при всех значениях х и не только при , то существует число

такое, что ряд абсолютно сходится при и расходится при .

Таким образом, решен вопрос об области сходимости степен­ного ряда. Интервал (R, R) называется интервалом сходимости степенного ряда. Число R называется радиусом сходимости сте­пенного ряда.

Отметим, что интервал сходимости некоторых рядов охваты­вает всю числовую прямую (в этом случае пишут ), у дру­гих вырождается в одну точку ( ). Итак, всякий степенной ряд имеет свой радиус сходимости R. При ряд может либо сходиться, либо расходиться. Этот вопрос решается для каждого конкретного ряда. Приведем способ определения радиуса сходимости степенного ряда.

Теорема 14. Если существует предел 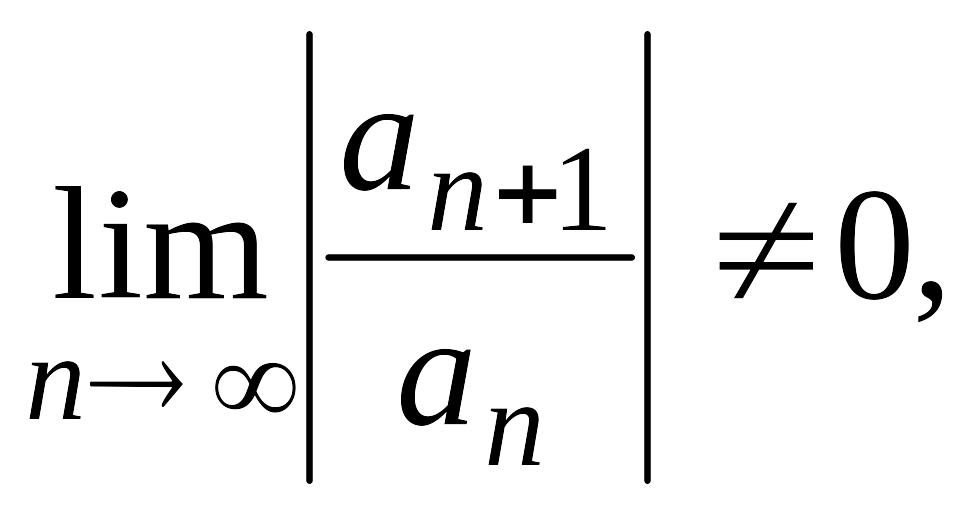то радиус сходимости ряда равен

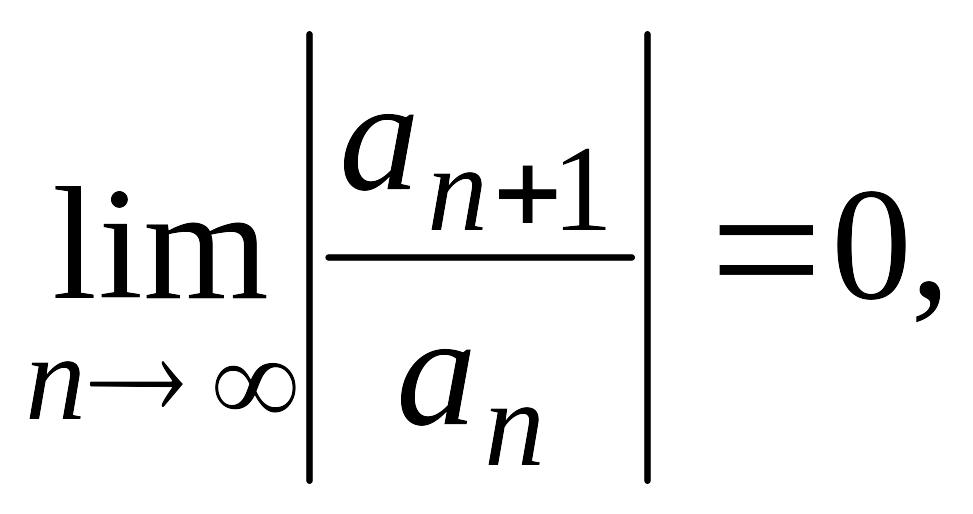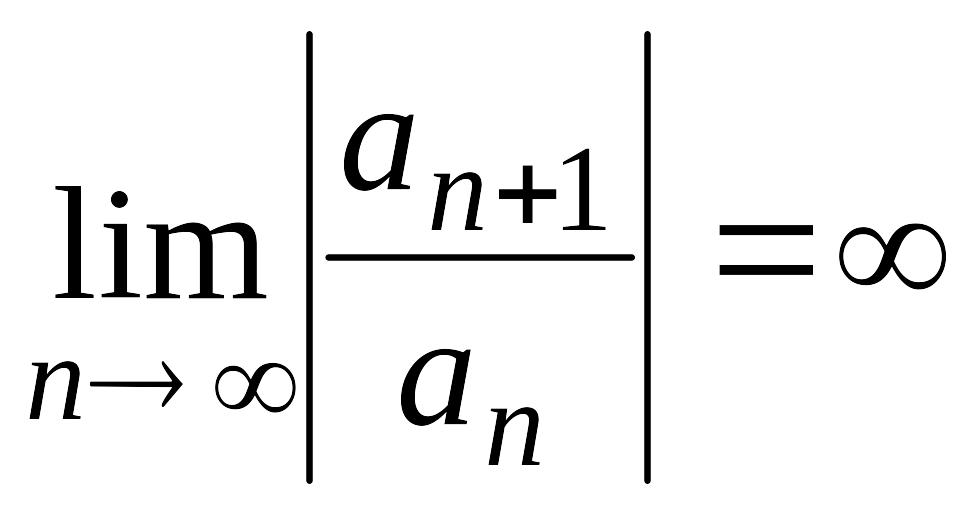З а м е ч а н и е. Можно доказать, что если то ряд сходится на всей числовой прямой, т. е , а если , то ряд сходится только при , т. е.

Пример 1. Рассмотрим ряд 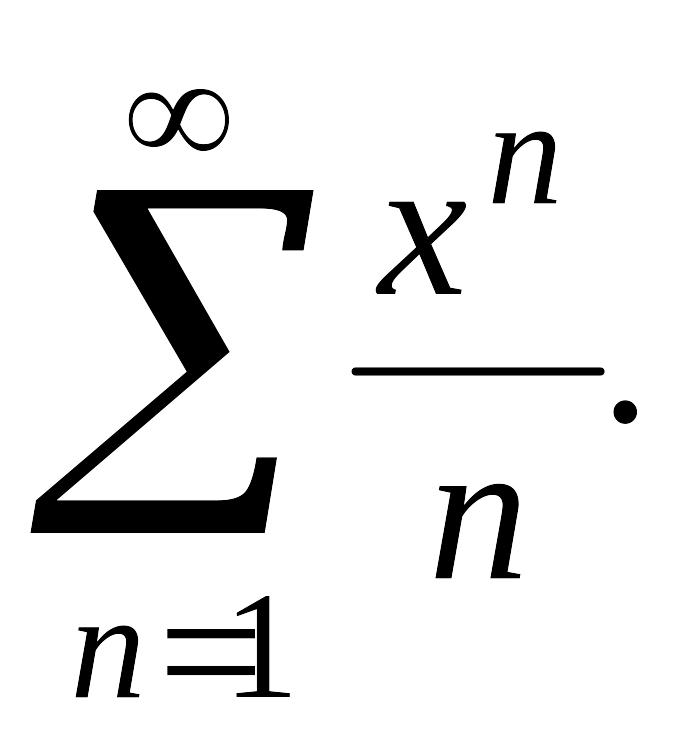Здесь и Поэтому

Следовательно, по теореме 13 данный ряд сходится на интер­вале Исследуем поведение ряда на концах интервала схо­димости, т. е. в точках . При получаем гармонический ряд , а при ряд 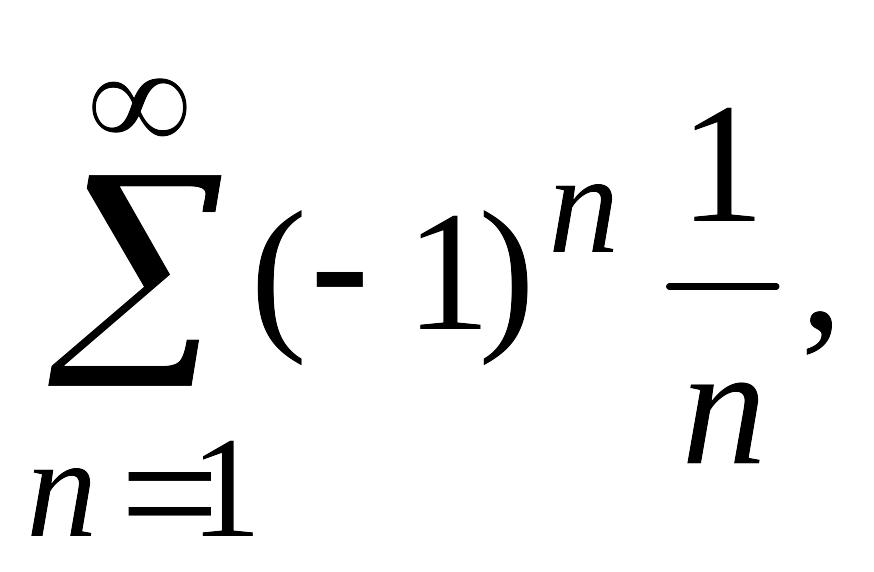который сходится в силу признака Лейбница. Таким образом, данный ряд сходится в любой точке полуинтервала [1, 1) и расходится вне его.

Пример 2. Ряд 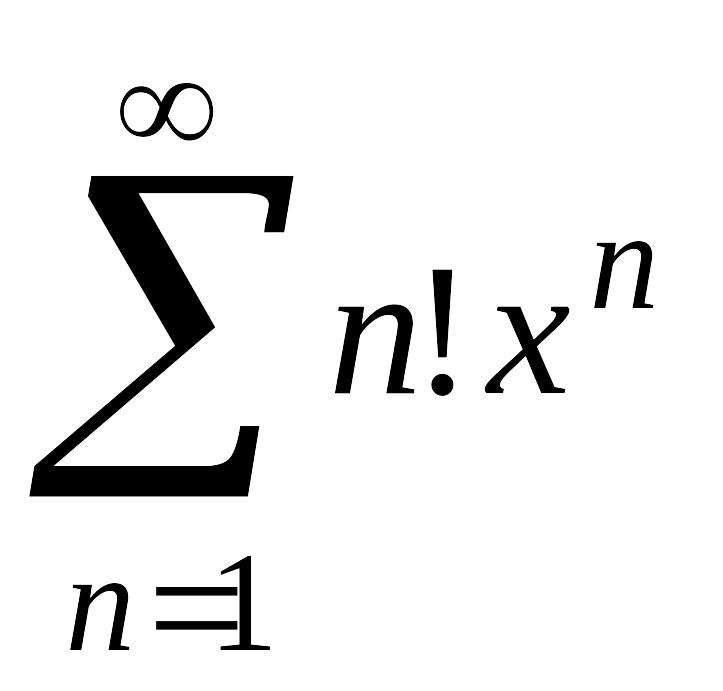расходится на всей числовой прямой, кроме точки , так как его радиус сходимости

Пример 3. Ряд сходится абсолютно на всей числовой прямой, так как его радиус сходимости

3. Свойства степенных рядов. Пусть функция является суммой степенного ряда

(4.10)

интервал сходимости которого . В этом случае говорят, что на интервале функция разлагается в степенной ряд (или ряд по степеням х).

Имеют место две теоремы о свойствах степенных рядов, которые приведем без доказательства.

Теорема 15. Если функция на интервале разлагается в степенной ряд (4.10), то она дифференцируема на этом интервале и ее производная может быть найдена почленным дифференцированием ряда (4.10), т. е.

.

Аналогично могут быть вычислены производные любого порядка функции . При этом соответствующие ряды имеют тот же интервал сходимости, что и ряд (4.10).

Теорема 16. Если функция на интервале разлагается в степенной ряд (4.10), то она интегрируема в интервале и интеграл от нее может быть вычислен почленным инте­грированием ряда (4.10), т.е. если то

.

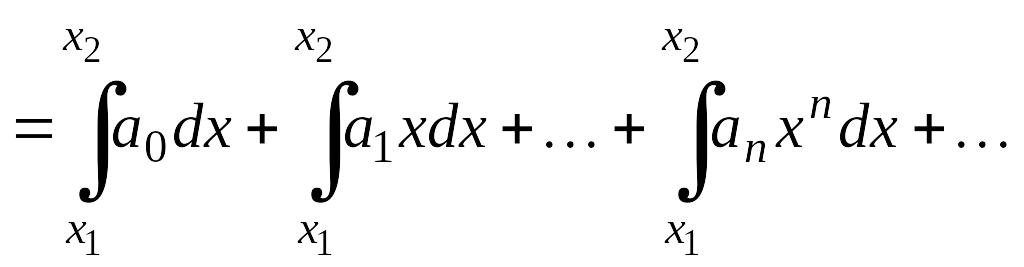Представляет интерес интегрирование степенного ряда (4.10) по отрезку , где :

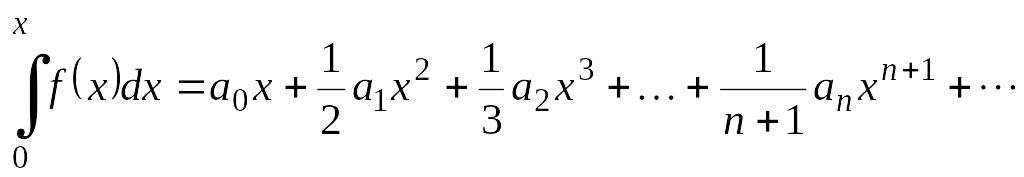
В этом случае опять получаем степенной ряд, который имеет тот же интервал сходимости, что и ряд (4.10).

Сформулированные теоремы дифференцирования и интегрирования степенных рядов имеют важное значение. Далее они неодно­кратно используются.

Отметим, что в ряде случаев рассматриваются степенные ряды более общего вида:

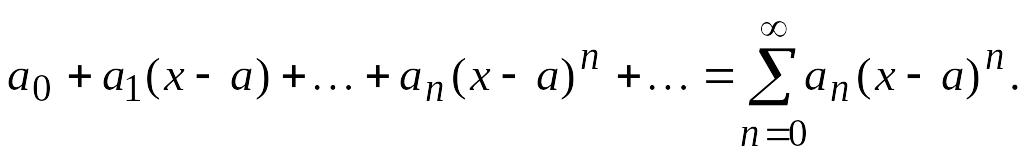(4.11)

Ряд вида (4.11) приводится к виду (4.9) заменой переменной .

Если функция является суммой ряда (4.11), то в этом случае говорят, что функция разлагается в ряд по степеням .

Все изложенное полностью переносится и на ряды вида (4.11). Для простоты записи последующие рассуждения проводятся для рядов вида (4.9).

4. Разложение функций в степенные ряды. Как показывает следующая теорема, разложение функции в степенной ряд един­ственно.

Теорема 17. Если функция на интервале разлагается в степенной ряд

(4.12)

то это разложение единственно.

Если функция разлагается в степенной ряд, то этот ряд имеет вид

(4.13)

Ряд (4.13) называется рядом Маклорена для функции .

Пусть теперь  произвольная бесконечно диффе-ренциру­емая функция. Для нее можно составить ряд (4.13). Установим, при каких условиях сумма ряда (4.13) совпадает с функцией . Ответ на этот вопрос можно получить с помощью формулы Маклорена. Ранее было показано, что для любой бесконечно дифференци­руемой функции справедлива формула Маклорена

,

где остаточный член имеет вид

(4.14)

Имеет место следующая теорема.

Теорема 18. Для того, чтобы ряд Маклорена (4.13) сходился на и имел своей суммой функцию , необходимо и достаточно, чтобы на остаточный член формулы Маклорена (4.14) стремился к нулю при , т. е. для любого (R, R).

Из теоремы вытекает, что вопрос о разложении функции в ряд Маклорена сводится к исследованию поведения остаточного члена при .

Рассмотрим разложения в ряд Маклорена некоторых элементарных функций.

Р а з л о ж е н и е ф у н к ц и и . Имеем: , откуда при получаем: . По формуле

(4.13) для функции составим ряд Маклорена:

. (4.15)

Найдем интервал сходимости ряда (4.15)

.

Следовательно, ряд абсолютно сходится на всей числовой прямой.

Докажем теперь, что функция  сумма ряда (4.15).

Отметим, что в силу необходимого условия сходимости ряда для любого х справедливо равенство

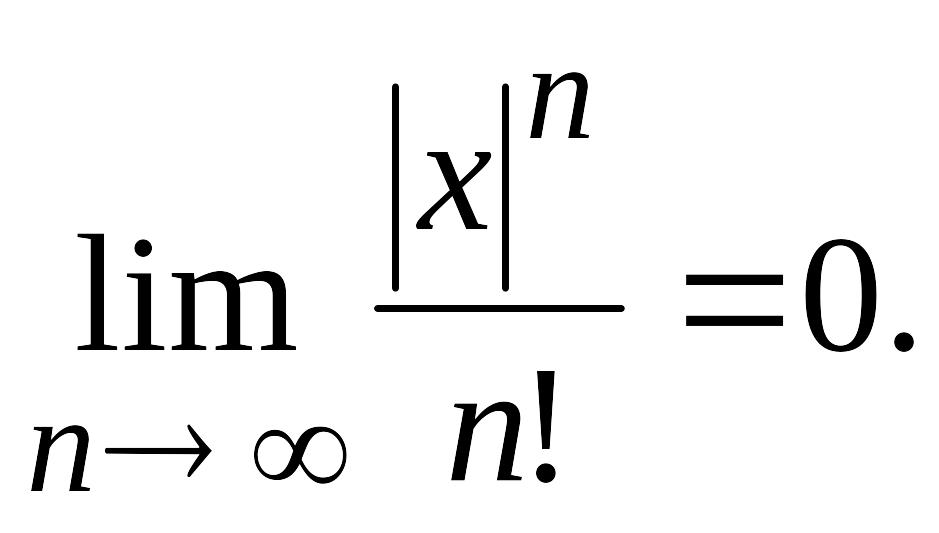(4.16)

Так как , то

где . Отсюда, учитывая, что ,

получаем

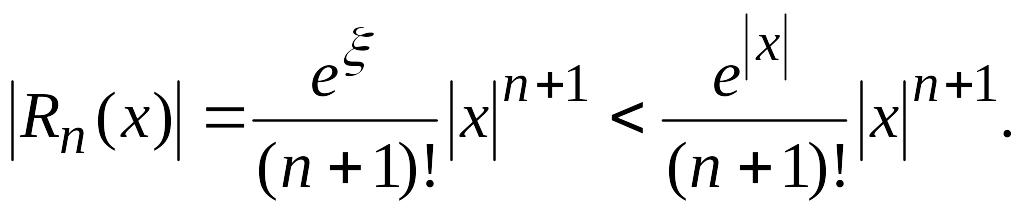
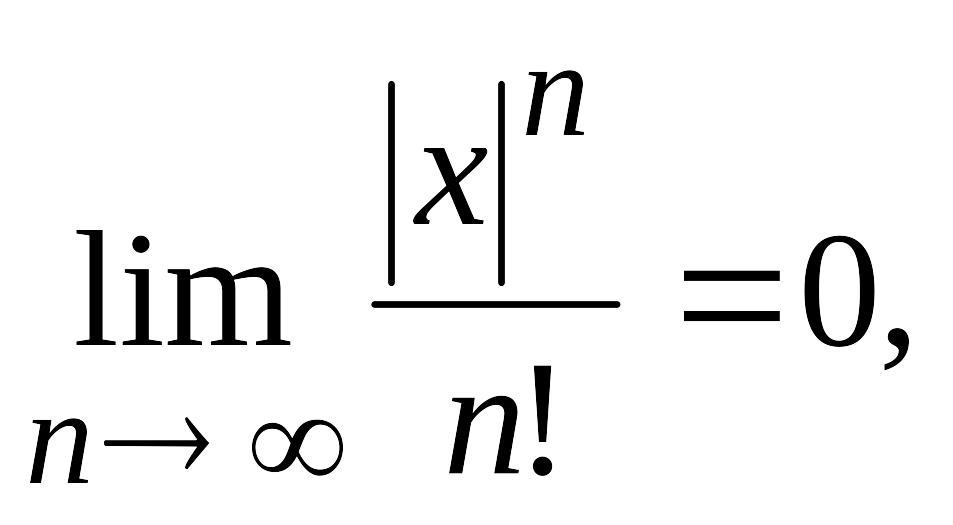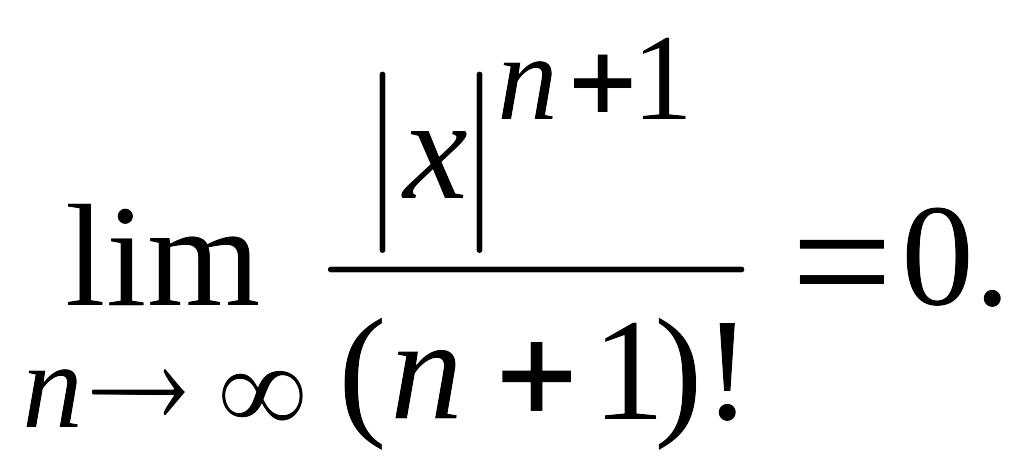Так как в силу (4.16) то и Поэтому, переходя к пределу в последнем неравенстве при , получаем, что при любом х, и, следовательно, функция является суммой ряда (4.15).