4.5 Интерполяция Эрмита
При построении интерполяционного многочлена Эрмита требуется, чтобы в узлах совпадали с табличными данными не только его значения, но и значения его производных до некоторого порядка. Пусть даны узлы x1, x2,…, xn и соответствующие системы чисел
,
,
………………..
.
В теории численных методов доказывается, что может существовать только один многочлен Hm–1(x) степени не выше m–1, где m=1+2+…+n, удовлетворяющий условиям
, r=0,
1, …, k–1,
k=1,
…, n.
Многочлен
Hm–1(x)
называют многочленом Эрмита, а узел xk
– узлом интерполирования кратности
k.
Многочлен Эрмита интерполирует функцию
f(x),
если
(r=0,
1, …, k–1,
k = 1,
…, n).
В общем случае выражения для многочленов Эрмита очень громоздко, и пользоваться ими на практике трудно, разве что за исключением простейших случаев. Однако возможности современных систем компьютерной математики позволяют без особых затрат программно организовать вычисление таких многочленов. Продемонстрируем некоторые такие приемы в системе Maple.
Пример. Построить многочлен наименьшей степени, принимающий в данных точках сам и для своей производной следующие значения
x |
0.5 |
2 |
3 |
4 |
5 |
f(x) |
0.3 |
1 |
2.2 |
2 |
1 |
f(x) |
0.2 |
0.9 |
1 |
–1.1 |
–0.3 |
> restart;
Вводим исходные данные – узлы интерполяции (массив X), значения в них функции (массив Y) и её производной (массив DY):
> X:=[0.5,2,3,4,5];Y:=[0.3,1,2.2,2,1]; DY:=[0.2,0.9,1,-1.1,-0.3];
> n:=5; m:=2*n; # n – число узлов интерполяции
Определяем аппроксимирующую функцию – алгебраический многочлен минимально возможной степени 2n–1 (почему?), но с пока неопределенными коэффициентами c[k]:
> h:=x->sum(c[k]*x^(k-1),k=1..m);
Формируем уравнения сначала из условия равенства значения полинома в узлах значениям функции f(x):
> eqns1:=(h(X[i])=Y[i])$i=1..n;
а затем то же для производных –
> eqns2:=(D(h)(X[i])=DY[i])$i=1..n;
Решаем полученную систему относительно коэффициентов многочлена:
> rez:=solve({eqns1,eqns2},{c[i]$i=1..m});
Подставив эти числа в h(x), результат сохраняем в виде новой функции hermite:
> hermite:=unapply(subs(rez,h(x)),x);
Это и есть искомый многочлен Эрмита. Выведем его график:
> g6:=plot(hermite(x),x=X[1]..X[n],color=black):
> g2:=plot([[X[i],Y[i]]$i=1..5],style=POINT,symbol=CIRCLE):
> plots[display](g2,g6);
Рис. 4.5.
Нетрудно видеть, что приведенный алгоритм эрмитовой интерполяции легко модифицируется на случай, если производная аппроксимируемой функции известна не во всех узлах, а лишь в некоторых, а также, если в них заданы производные более высокого порядка. Но на практике такого рода (глобальная) интерполяция Эрмита используется редко из-за слишком высокой степени полинома уже при небольшом числе узлов. Зачастую лучший результат обеспечивает локальная интерполяция, т. е. когда производится интерполирование на отдельных отрезках изменения x полиномами малой степени.
Рассмотрим локальную интерполяцию Эрмита по заданным значениям функции и её производной. На каждом отрезке [xk, xk+1] имеем по два значения функции и производной на концах отрезка, тем самым по ним можно построить полином 3-й степени
,
xk
x
xk+1,
который должен удовлетворять условиям
,
,
,
.
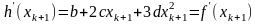Эта система уравнений замкнутая, её можно разрешить относительно четырех коэффициентов a, b, c, d и в итоге получить многочлен Эрмита на k-м отрезке. Проделав эту процедуру n–1 раз, найдем полную интерполирующую функцию на всём отрезке [x1, xn].
Вот как это можно сделать в Maple.
> restart;
> X:=[0.5,2,3,4,5]: Y:=[0.3,1,2.2,2,1]: # табличные данные
> DY:=[0.2,0.9,1,-1.1,-0.3]: n:=5:
> p:=array(1..n-1); # выделение памяти под массив
> for k from 1 to n-1 do # цикл по частичным отрезкам
h:=x->a+b*x+c*x^2+d*x^3; # кубический полином
r:=solve({h(X[k])=Y[k],h(X[k+1])=Y[k+1],
D(h)(X[k])=DY[k],D(h)(X[k+1])=DY[k+1]},
{a,b,c,d});# решение системы 4 уравнений
p[k]:=subs(r,h(x)); # запись локального многочлена Эрмита в массив
od: # конец цикла (в более поздних версиях Maple вместо od используется end do)
> w:=unapply(piecewise(x<X[2],p[1],x<X[3],p[2],
x<X[4],p[3],p[4]),x); # создание аппроксимирующей функции путем сшивки ее локальных частей
> evalf(w(x),5);# просмотр этой аппроксимирующей функции
> g7:=plot(w(x),x=0.4..5.1,color=black): # график этой функции на отрезке [0.4, 5.1]
> g2:=plot([[X[i],Y[i]]$i=1..n],style=POINT, symbol=CIRCLE):
> plots[display](g2,g7);
Рис. 4.6.
> [D(w)(0.5),D(w)(3),D(w)(4)]; # проверка значений производной в ряде узлов
