1.5. Действующий элемент системы

Как было ранее отмечено, объект, выполняющий определенные системные функции и не подлежащий дальнейшему расчленению в рамках морфологического описания, принимается в качестве «первичного» элемента системы (рис. 1.9). Связь элемента с внешней средой, к которой относятся и другие элементы системы, осуществляется через его входы ͞x=(x₁,x₂,….,x_m) и выходы ͞y=(y₁,y₂,….y_n).Через ͞х элемент подвергается внешним воздействиям, а через ͞y сам воздействует на внешнюю среду.

Рис. 1.9. Схематичное представление элемента системы

Такое представление предполагает наличие у элемента по крайней мере одного входа и одного выхода.

Поведение элемента будем рассматривать как последовательную смену его «внутреннего» состояния в некотором интервале времени. Такая динамика (динамический процесс), как правило, описывается системами дифференциальных или конечно-разностных уравнений.

В общем случае описание можно представить как

u_t^’=f[͞u(t), ͞x(t),t] , ͞u(0)=͞u₀;

y(t)=h[͞u(t), ͞x(t),t],

где (t) – р-мерный вектор, компоненты которого описывают состояние элемента в момент времени t; ͞u₀ – начальное состояние элемента; у(t) – n-мерный вектор выходов элемента; ͞x(t) – m-мерный вектор входов элемента.

В дискретные моменты времени динамика может быть представлена как система разностных уравнений вида

где k = 0,1,2,3,,.. – порядковый номер, характеризующий последовательное дискретное время.

Заметим, что состояние элемента в каждый момент времени можно интерпретировать как некоторую точку в р-мерном пространстве состояний (фазовом пространстве). Тогда поведение элемента во времени можно представить в виде некоторой траектории (фазовой траектории) в пространстве состояний, которая описывается вектором функцией ͞u(t).

Изучая элемент с позиций описания взаимодействия вход-выход, можно считать некоторым преобразователем входов в выходы в соответствии с правилами, определенными внутренним описанием:

͞y (t)=R(t) (͞x(t)), (1)

где R(t) – символическое обозначение совокупности преобразования входа в каждый выход (оператор преобразования).

В частном случае при t= const (t→∞):

͞y(t)= R(x). (2)

Системный элемент, обладающий вышерассмотренными свойствами, будем называть действующим элементом системы.

Например, предположим, что оператор R – линейный (линейное преобразование). Соотношения (1)-(2) можно записать как ͞у =A*k, где , ; – матрица линейного преобразования:

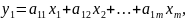
или

Связь действующих элементов. Пусть Е₁и Е₂ – два действующих элемента с операторами R₁ и R₂ соответственно, ͞x₁=(x₁₁,x₁₂,….,x_1m1) и ͞x₂=(x₂₁,x₂₂,….,x_2m2) – их входные векторы, а ͞y₁=(y₁₁,y₁₂,….,y_1m1) и ͞y₁=(y₂₁,y₂₂,….,y_2m1) – выходные векторы.

Элемент E₁ воздействует на элемент Е₂ только таким образом, что Е₂ через свои входы «принимает» значения всех или нескольких выходов элемента Е₁.

Тогда можно записать:

x_2j= y_1i (3)

для некоторых значений i и j , где ; . Очевидно, что равенство (3) должно быть выполнено хотя бы для одной пары значений ( i ,j ) иначе не было бы воздействия элемента E₁ на элемент E₂.

Введем квадратную матрицу S₂₁, состоящую из m₂ или n₁ строк и столбцов в зависимости от того, m₂≥ n₁ или n₁ ≥ m₂. Элементы S_ij матрицы определяются следующим образом:

Другими словами, элементы матрицы имеют значение I, если соответствующая составляющая вектора ͞y элемента Е₁ принимается в качестве составляющей вектора входа ͞х₂ элемента Е₂ , и 0, если этого не происходит. Матрица S₂₁ примерно имеет вид:

S₂₁ – нуль-единичная матрица, если хотя бы один ее элемент не является нулем.

Матрицу S₂₁ назовем матрицей связи элемента Е₂ с элементом Е₁ (рис. 1.10). С ее помощью система равенств (3) записывается как ͞x₂=s₂₁y₁.

Рис. 1.10. Схематическое представление связи двух действующих элементов

Матрицу связи элементов можно обобщить для любых элементов системы E_r и E_k независимо от того, связан E_r с E_k или нет. Если элемент E_r не связан с E_k , то соответственно S_kr= 0 (0 – нулевая матрица, все ее элементы равны 0). С другой стороны, если S_kr имеет все ненулевые элементы, то это означает, что каждая координата вектора ͞х_k связана со всеми координатами вектора ͞y_r. В общем случае

͞x_r=S_kr͞y_k. (4)

Допустим, что система состоит из N элементов E₁, E₂ ,…, E_rn, которые описаны входными векторами и выходными векторами, соответственно ͞х₁ , ͞x₂, … ͞x_n и y₁,͞y₂,…,͞y_n.Тогда для каждой пары элементов можно записать векторное соотношение связи типа (4). В результате получается N (N-1) векторных равенств:

͞x_r=S_kr͞y_k,

, , (5)

Сформированные таким образом матрицы связи образуют в совокупности квадратную матрицу размером N на N вида

Матрицу S назовем матрицей связей системы в целом. Она характеризует сеть связей между всеми элементами системы и практически выражает структуру.

Матрица S является нуль-единичной, так как все нуль-единичные матрицы связей S_kr выступают в виде ее элементов.

Исходя из вышеизложенного, взаимодействие любых двух элемента E_r и E_k можно представить в виде векторных равенств:

x_r=S_krR_k(͞x_k),

͞y_r=R_r(͞x_r), , , (6)

где R_k и R_г – операторы преобразований для элементов Е_к и E_r соответственно.

Обобщая способ действия (6) на всю систему, получим:

X*=R*S(X); Y*=S*R(Y), (7)

где X, Y – состояние входов и выходов системы до преобразования; X*, Y* – новое состояние входов и выходов системы после преобразования; R – матрица операторов преобразования отдельных элементов; S – матрица связей между элементами.

Таким образом, соотношения (6) и (7) позволяют формально описывать действие системы в целом через действия отдельных ее элементов, образующих структуру систем.