3.2. Общая задача нелинейного программирования. Постановка задачи

Не теряя общности, рассмотренные выше модели оптимизации сводятся к так называемой задаче нелинейного программирования (НП). Эту задачу будем записывать следующим образом:

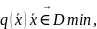
(26)

где функции – в общем случае нелинейные.

Если функции q, h_k (k=͞1͞,P) линейны по ͞x, то задача (26) – задача линейного программирования.

В (26) функция q( ͞x) называется критерием оптимизации (целевой функцией), функция h_k(͞x) (k = ͞1͞,͞Р) – функцией ограничений, область D – областью допустимых решений; х D – допустимым решением (вектором, точкой). Допустимое решение, минимизирующее целевую функцию q( ͞x), называется оптимальным решением, а соответствующее ему значение функции q( ͞x) – оптимальным значением.

Предположим, что в задаче НП (26) ограничения в области D заданы в виде равенств, то есть h_k(͞x) =0, k = ͞1͞,͞Р.

Очевидно, что такая задача является частным случаем, так как каждое равенство h_k(͞x) =0 можно заменить двумя неравенствами h_k(͞x) ≤ 0, -h_k(͞x) ≤0, а ограничения неравенства представимы в форме равенств введением дополнительных переменных z_k так, чтобы h_k(͞x)+z_k=0, k=͞1͞,͞P.

Следует помнить, что задачу максимизации также можно записать в виде задачи НП (26), заменив q( ͞x) на -q ( ͞x).

Геометрия поиска. Состояние объекта оптимизации (ТП) характеризуется вектором ͞X = (x₁,…x_m), который в m-мерном пространстве переменных определяет точку с координатами x₁,x₂,….x_m. Функция q в каждой точке пространства имеет определенное значение, причем имеются поверхности равного уровня. Вспомним, что такие поверхности определяются равными значениями критерия оптимизации q, уравнения которых записываются в виде

(27)

где с – значения критерия оптимизации.

При m = 2 уравнения (27) образуют так называемые линии уровня (рис. 3.3).

a б

Рис. 3.3. Образование линий уровня: ͞X*= (x₁*, x₂*) – оптимальное решение:

а – общее; б – проекция на плоскость

Рассмотрим теперь, как в пространстве параметров ͞х представляются ограничения. Ограничения типа равенств h_k(x₁,…x_m)=0, k=͞1͞,͞P уменьшают размерность пространства параметров, так как переменные x₁,…x_m, могут выбираться на поверхности, определяющейся пересечением гиперповерхностей h_k(͞x), k =1͞,͞Р, всех ограничений одновременно. Например, при m = 3 решение находится на поверхности h (x₁, х₂,x₃) =0, которая и определяет двухмерное пространство оптимизируемых параметров (рис. 3.4).

Рис. 3.4. Пример ограничений типа равенств: ͞x* – оптимальное решение

Ограничения типа неравенств образуют (высекают) в х-мерном пространстве параметров сферический многогранник, определяющий область допустимых решений D.

Уравнения h_k( ͞x)=0 являются уравнениями границы, разделяющей пространство параметров на две части – в одной из них h_k( ͞x) ≤ 0, в другой – h_k( ͞x) >0. Сказанное иллюстрирует рис. 3.5.

Рис.3.5. Пример ограничений типа неравенств: q₁>q₂>q₃>q₄; ͞

x* – оптимальное решение; ОАВСЕ – область допустимых решений

Здесь нанесены линии уровня для функции q( , ), область допустимых решений:

При этом минимум показателя качества (критерия) достигается на границе области D. Необходимо знать, что в зависимости от вида критерия оптимизации q экстремум (максимум или минимум) может быть локальным, глобальным, внутренним, граничным, условным и безусловным.

В точке ͞x* достигается локальный минимум, если q(͞x*) есть наименьшее значение функции q(͞x) в некоторой Ԑ-окрестности этой точки. Наименьший из всех локальных минимумов называется глобальным. Понятно, что если во всей области D имеется один локальный минимум, то он будет глобальным (см. рис. 3.3, 3.4, 3.5).

В этом случае критерий оптимизации q(͞x) называется циклоидальным (одноэкстремальным). Если q(͞x) в области D имеет несколько локальных минимумов, то он называется многоэкстремальным (рис. 3.6).

A

x₂

x₁

B

2

4

6

9

3

5

7

8

10

10

x₁^A

x₁^B

x₂^A

x₂^B

Рис. 3.6. Линии уровня функции q(x₁x₂) с двумя локальными минимумами:

q(A)=2; q(B)=0 – глобальный минимум

Предположим, что в некоторой подобласти

задачи НП функция q(͞x) унимодальна с локальным минимумом в точке ͞ .

Также будем считать, что одним из методов оптимизации можно решить задачу и найти соответствующую точку локального минимума .

Надо знать, что в этом случае методы такой оптимизации называются методами локального поиска, а подобласти δ_ρ – областями притяжения локального минимума в точках ͞ . Решение же многоэкстремальной задачи при таких предположениях может быть сведено к решению β-задач на локальный экстремум.

Экстремумы называются граничными, если они достигаются в граничных точках области D (см. рис. 3.5), и внутренними, если они достигаются во внутренних точках области D (см. рис. 3.4).

Если экстремумы критерия q(͞x) ищутся в условиях отсутствия ограничений на вектор ͞х, то они называются безусловными (см. рис. 3.3, 3.6), в противном случае – условными (см. рис. 3.4, 3.5).

Одной из важных геометрических характеристик многомерной функции q(͞x) является ее градиент. Вспомним, что градиент аналитически определяется следующим образом:

. (28)

Следует помнить, что градиент скалярной функции q(͞x) в некоторой точке ͞x_k – это вектор, направленный в сторону наибольшего увеличения функции и ортогональный поверхности (линии) уровня в точке ͞x_k. Противоположный вектор называется антиградиентом. Он направлен в сторону наискорейшего убывания функции q(͞x) в точке (рис. 3.7).

Рис. 3.7. Геометрическая интерпретация градиента в точке x:

q1>q2>q3 >…. ; ͞x* – оптимальное решение

Из (28) следует, что вектор grad q(͞x) можно получить для широкого класса аналитически заданных функций q(͞x) путем вычисления соответствующих частных производных dq/dx, i=͞1͞,͞m. Однако в практических задачах такой подход обычно невозможен, так как здесь, с одной стороны, функции q(͞x) как правило, не дифференцируемы, имеют громоздкие формулы расчета, иногда вычисляются при помощи моделируемых алгоритмов и др., с другой стороны, практические задачи решаются на ПК. Это требует применения разностных методов для приближенной оценки частных производных. Рассмотрим два таких метода:

(29)

(30)

где ͞x_k=(x₁^kx₂^k …., x_i^k, x_m^k ) – k-я точка, в которой вычисляется градиент, x_i – величина шага по i-й координате в окрестности точки x.

Показано, что точность формулы (30) для приближенного вычисления частных производных выше, чем формулы (29). Однако для ее использования требуется большее число арифметических вычислений (практически в два раза). Это необходимо учитывать при достаточно сложном выражении для критерия оптимизации q(͞x).

Численная схема отыскания экстремума. Следует помнить, что существуют два подхода к решению задачи НП типа (26). Первый (классический) заключается в замене задачи на экстремум задачей поиска решений системы уравнений вида

(31)

При нахождении безусловного экстремума (ограничения отсутствуют)

(32)

где λ=( λ₁…. λ_k) – вектор произвольных множителей, если ограничения заданы в виде равенств.

В (32) L = L ( ͞x , ͞λ) называется функцией Лагранжа. Оптимизация здесь сводится к решению систем m+р уравнений относительно неизвестных … , λ₁…. λ_p.

Второй подход связан с так называемыми численными методами поиска (поисковыми методами). Здесь требуется построить оценку ͞ D оптимального решения ͞x* (предполагается, что оно существует) на основе конечного числа k значений функции q(͞x), последовательно вычисляемых в точках x₀,x₂…,x_k D, причем эти значения образуют убывающую сходящуюся последовательность q(͞x) >q(͞x1)>…. q(͞x2=͞x*). Последовательность называется релаксационной, а методы ее построения – методами спуска.

Тогда, в общем случае, можно предложить итерационную формулу построения

{ }:͞ =͞ +͞ ͞ -) k=0,1,2…, (33)

где ͞ – направления спуска, ͞ – длина шага спуска вдоль выбранного направления ͞ .

Степень близости оценки к оптимальному решению ͞x* в этом случае можно задать, например, в виде ||x*- || ≤ Ԑ или |q(͞x*)| - |q(͞ )| ≤ Ԑ, где Ԑ > 0 – заданная точность. Одним из показателей эффективности численных методов спуска может служить их скорость сходимости. Говорят:

о линейной сходимости (сходимость со скоростью геометрической прогрессии), если:

о сверхлинейной сходимости, если:

где µ→0, k→0;

о квадратичной сходимости, если:

На рис. 3.8 приведена схема вычислений для одной итерации такого поиска в соответствии с формулой (33).

Рис. 3.8. Схема одной итерации поиска: : = - знак присвоения