3.3. Градиентные методы

В рассматриваемых методах используются свойства градиента. Выбирая в формуле (33) в качестве направления спуска антиградиент, получим следующий итерационный процесс поиска в координатной форме:

(34)

где частные производные , вычисляются либо по формуле (29), либо (30); x_k=(x₁^kx₂^k …., x_i^k, x_m^k ).

Существуют различные способы выбора шага в формулах (34). При этом следует помнить, что, с одной стороны, длина шага не должна быть слишком большой, чтобы не «проскочить» экстремум (алгоритм может зациклиться), с другой – длина шага не должна быть и слишком малой, чтобы итерационная процедура оптимизации не оказалась медленная. Ниже рассмотрим два возможных способа выбора шага . Первый заключается в том, что фиксируется некоторое значение >0 и процедура оптимизации реализуется для k = 0,1,2,... с некоторой начальной точки ͞ такое число раз, пока не станет q(͞ ) ≥ q(͞ ). С этого момента для того, чтобы ближе подойти к минимуму, величина шага уменьшается, итерационная процедура (34) повторяется и т.д.

Второй способ – это так называемый метод наискорейшего спуска. Здесь на каждой итерации величина выбирается таким образом, чтобы в направлении спуска целевая функция достигала своего минимального значения. Другими словами, выбирается из условия

(35)

Такой подход на каждой итерации предполагает решать задачу скалярной (одномерной) минимизации (35) по переменной , которая может оказаться трудоемкой, особенно в условиях, когда вычисления функции сложны либо q(͞х) не дифференцируема и минимизация проводится перебором с некоторым шагом. В то же время метод наискорейшего спуска дает выигрыш в числе машинных операций, так как обеспечивает движение с самой выгодной величиной шага .

Следует помнить, что метод наискорейшего спуска в отличие от обычного градиентного с выбором по первому способу обеспечивает направление движения из точки ͞ по касательной к линии уровня в точке ͞ , причем звенья такого зигзагообразного спуска ортогональны между собой (рис. 3.9).

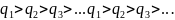
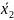
а б

Рис. 3.9. Траектория спуска: а – градиентный метод; б – наискорейший спуск

В общем случае считается, что в рассмотренных выше методах градиентного спуска последовательность точек {͞ } сходится к стационарной точке функции q(x).Можно доказать следующую теорему.

Теорема. Если функция q(͞x) ограничена снизу, ее градиент удовлетворяет условию Липшица:

где R – константа Липшица ͞х, ͞у E_n и выбор значения производится одним из описанных выше способов, то, какова бы ни была начальная точка, .

Теорема даёт практические условия прекращения итерационной процедуры поиска в виде

(36)

где δ > 0 – число, характеризующее точность нахождения минимума.

Пример.

В качестве начальной точки возьмём

Первая итерация. Вычислим градиент в точке ͞x₀: grad q(x) = (12,10,6). Сделаем шаг в направлении антиградиента из точки ͞х₀ в точку ͞х₁ .

Для этого используем формулы (34):

В нашем случае

(37)

Используем наискорейший спуск – выберем длину шага из условия (35):

Для нахождения минимума по переменной приравняем производную по этой переменной к нулю: -48 или после преобразований : .

Отсюда учитывая соотношения(37),

Здесь =(4,32; -6; 0,24).

Заметим, что с условиями (36):

Вторая итерация. Вновь по формулам (34):

или

,

Величину выбираем из условия

Приравнивая производную по α, к нулю и решая уравнение, получим α= 0,13. Тогда ͞ = (0,52; 0,18; 0,01); q(͞ ) = 0,7<q(͞ ) = 4,14<q(͞ )=26.

Как видим, с каждой итерацией q(͞ ) приближается к своему оптимальному значению, равному 0.

Можно показать, что градиентные методы имеют сходимость со скоростью геометрической прогрессии. Из рис. 3.10 видно, что чем ближе линии уровня функции q(͞x) к окружности, тем быстрее сходятся градиентные методы. В тех случаях, когда поверхности уровня сильно вытянуты (функция имеет так называемой «овражный» характер), этот метод может сходиться очень медленно и не обеспечить заданной точности поиска.

Рис.3.10. Траектории поиска методом наискорейшего спуска

Например, если точка минимума лежит на дне оврага (на узком гребне – если решается задача на максимум), то метод может вызвать прыжки через овраг (рис. 3.11).

Рис. 3.11. Градиентный поиск минимума овражной функции

Для ускорения поиска экстремума в этом случае используется так называемый овражный метод.

Опишем простейший его вариант. Из двух начальных точек ͞ и ͞ производится одним из градиентных методов спуск в точки ͞ и ͞ на дне оврага. Допустим, что при этом q( ͞ )<q(͞ ).

Далее делается движение по дну оврага, для этого полагается:

где h > 0 называется овражным шагом.

Из точки ͞ , которая, вообще говоря, находится на «склоне оврага», производится спуск на дно оврага в точку , определяется точка ͞х₃ и т.д. В общем, процесс движения по дну оврага описывается следующей итерационной формулой:

(38)

Если уже найдены , ͞ , то из точки осуществляют спуск и находится следующая точка на дне оврага (рис. 3.12).

Рис. 3.12. Овражный поиск минимума

(спуск из точек и схематично изображен в виде отрезка прямой)

Величина h на каждой итерации поиска подбирается эмпирически в зависимости от информации о поведении минимизируемой функции. При этом необходимо помнить, что величину овражного шага требуется выбирать так, чтобы по возможности быстрее проходить прямолинейные участки на «дне оврага» за счет увеличения овражного шага; на крутых поворотах за счет уменьшения шага избежать выброса из «оврага»; добиться меньшего отклонения точек ͞ от «дна оврага» и тем самым сократить объем вычислений в процедурах градиентного спуска.

Учет ограничений. Ограничения в задаче НП создают дополнительные трудности в процессе поиска минимума (максимума). Будем рассматривать ограничения в виде неравенств (͞x)≤0, k=͞1͞, P, которые могут также выступать в качестве выходов ТП.

Необходимо помнить, что для достижения минимума не обязательно двигаться в направлении градиента, а можно осуществлять поиск по любому направлению, вдоль которого функция q(͞x) убывает. Поэтому, если в процессе движения к оптимуму встретилось ограничение (граница) допустимой области решений D, поиск можно продолжать вдоль этой границы. Одним из простейших способов такого движения является зигзагообразное движение, в этом случае при нарушении ограничений следует оптимизацию проводить не по функции q(͞x), а по k нарушенным ограничениям, минимизируя сумму q̂(͞x)=∑ (͞x), (k≤p). Определяя антиградиент этой суммы (-gradq̂(͞x)), организуют движение в направлении этого антиградиента, и тем самым производится возврат в область допустимых решений D.

Такой подход эквивалентен минимизации некоторой функции Q(͞х) следующего вида:

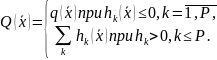
На рис. 3.13 показан пример такого поиска минимума.

0

Рис. 3.13. Работа градиентного метода в условиях ограничений