12.2.Формула Эйлера для критической силы

Рассмотрим шарнирно опертый по концам сжатый стержень (рис. 12.2). Предположим, что по какой-то причине стержень получил малое искривление оси, вследствие чего в нем появился изгибающий момент M=Fv.

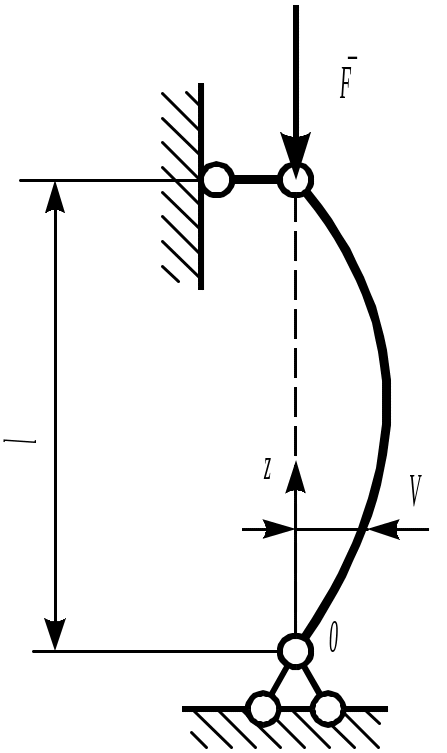
Рис. 12.54

При малых прогибах справедливо равенство EIv”= – M, которое можно представить в виде:

V”+k²v=0, (12.2)

где обозначено k²=F/EI.

Решение однородного дифференциального уравнения (2) имеет вид

V(z)=Bcoskz+Csinkz.

Произвольные постоянные B и C определяются из граничных условий:

при z=0 v=0;

при z=l v=0.

Из первого условия следует, что B=0. Таким образом, уравнение оси изогнутого стержня записывается так:

v=Csinkz.

Используя второе граничное условие, получим

Csinkl=0.

Если предположить, что C0, то sinkl=0 и тогда получим kl=n, n=1,2,3,… .

В результате имеем F=n²²EI/l², т.е. криволинейная форма равновесия стержня возможна только при фиксированных значениях сжимающей силы. При n=1 стержень изгибается с образованием одной полуволны синусоиды (рис. 12.3), при всех последующих n число полуволн соответственно равно n.

Наименьшее значение сила F принимает при n=1

F_кр=²EI/l². (12.3)

Рис. 12.55

Эта сила называется критической силой. Формула (12.3) была впервые получена в 1744 г. математиком Леонардом Эйлером.

Таким образом, F_кр представляет собой наименьшую сжимающую силу, при которой наряду с прямолинейной формой равновесия становится возможной другая (изгибная) форма равновесия.

12.3.Влияние способа закрепления концов стержня на значение критической силы

Формула Эйлера получена для шарнирного опирания стержня по концам. На практике встречаются и другие способы закрепления концов (рис. 12.4).

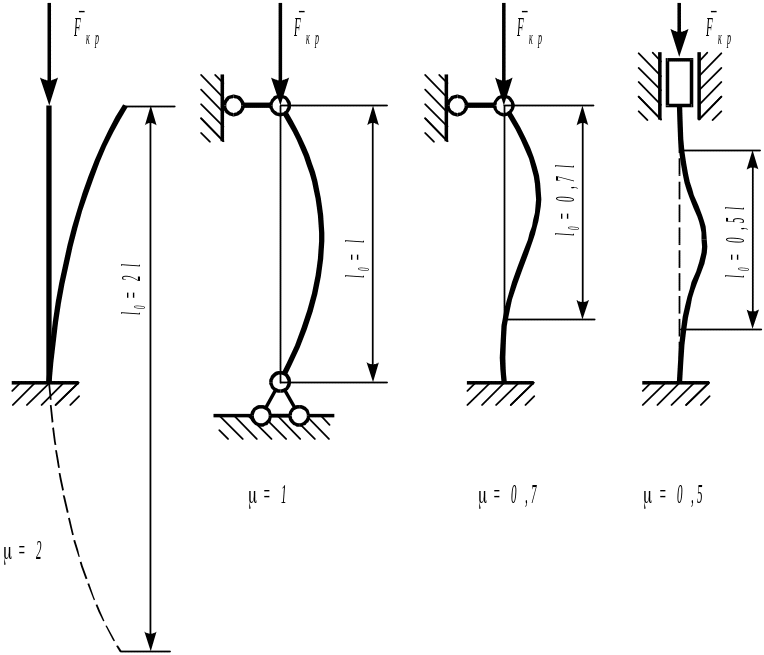
Рис. 12.56

Критическая сила для каждого из этих стержней может быть получена по обобщенной формуле:

F_кр=²EI/(l)²,

где -коэффициент приведенной длины, а величина l=l₀ называется приведенной или свободной длиной.

12.4.Практический расчет сжатых стержней

Найти значение критической силы для двутаврового стального стержня, защемленного нижним концом (рис. 12.5).

Из ГОСТ 8239-89 моменты инерции и площадь поперечного сечения двутавра №30 равны: I_x=7080 см⁴, I_y=337 см⁴, А=46,5 см². Модуль упругости стали Е=2,0610⁵Мпа. Коэффициент свободной длины =2.

Потеря устойчивости стержня произойдет в плоскости наименьшей жесткости стержня, поэтому при вычислении критической силы следует брать наименьший момент инерции поперечного сечения.

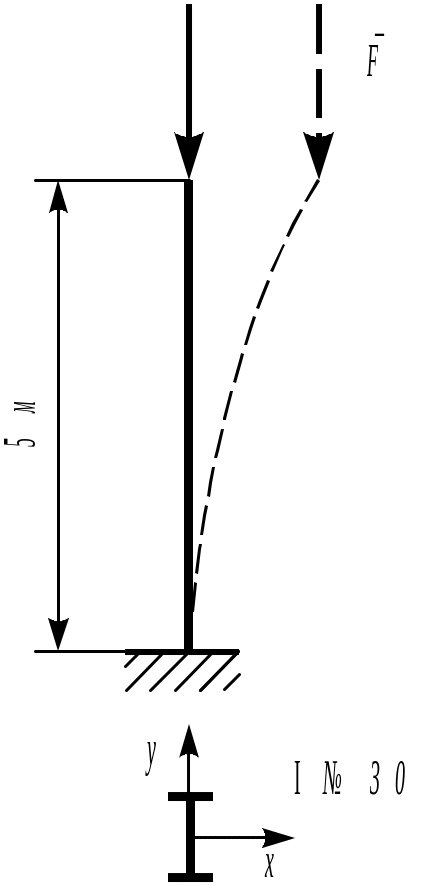
Рис. 12.57

В результате найдем

F_кр=²TI_y/(l)²=3,14²2,0610⁵10⁶33710^-8/(25)²=68447 Н.

Нормальные напряжения в поперечном сечении стержня, возникающие при действии этой сжимающей силы, равны:

кр=Fкр/A=68447/(46,510-4)=14,7Мпа.

Отсюда видно, что потеря устойчивости стержня наступает при напряжениях, значительно меньших предела текучести или предела прочности материала. Действительная сжимающая сила, прикладываемая к стержню, должна быть меньше полученной критической силы.

13.Теория тонких пластин

13.1.Основные понятия и гипотезы

Пластинкой называется призматическое или цилиндрической тело, высота которого мала по сравнению с размерами в плане (рис. 13.1). Высота называется толщиной пластинки и обозначается h.

Рис. 13.58

Плоскость, делящая пластинку пополам по толщине, называется срединной. Составляющая перемещения w в направлении оси z будет представлять собой прогиб пластинки. Пластинки находят широкое применение в строительстве в виде настилов и панелей, железобетонных плит для покрытия производственных зданий, плит фундаментов массивных зданий. Расчетной схемой плит, применяемых в строительных конструкциях, является тонкая пластинка.

Тонкими называются пластинки, имеющие отношение толщины к наименьшему характерному размеру в плане h/b примерно в пределах 1/5 – 1/80 и величину ожидаемых прогибов не более h/4.

Тонкие пластинки рассчитывают по приближенной теории, которая основана на следующих гипотезах, предложенных немецким физиком Г.Кирхгофом.

1. Гипотеза прямых нормалей: любой прямолинейный элемент, нормальный к срединной плоскости, остается прямолинейным и нормальным к срединной поверхности после деформирования пластинки, и длина его не изменяется.

2. Гипотеза о недеформируемости срединной плоскости: в срединной плоскости отсутствуют деформации растяжения, сжатия и сдвига, т.е. она является нейтральной и ее перемещения u₀= v₀=0.

3. Гипотеза об отсутствии давления между слоями пластинки, параллельными срединной плоскости. Гипотеза позволяет пренебрегать напряжением _z ввиду малости по сравнению с напряжениями _x и _y.