6.1. Классификация функций

Постоянная функция f (x) = C, C = const, степенная функция х^ (  – любое число), показатель­ная функция а^х ( 0 < а ≠ 1), логарифмическая функция log_а x (0 < а ≠ 1), тригонометрические функции: sin x, cos x, tg x, ctg x и обратные тригонометрические функции: arcsin x, arccos x, arctg x, arcctg х называются простейшими элементарными функциями.

Все функции, получаемые с помощью конечного числа ариф­метических действий над простейшими элементарными функциями, а также суперпозицией (или наложением) этих функций, состав­ляют класс элементарных функций.

Примерами элементарных функций являются:

и т.д.

Имеет место следующая классификация элементарных функций.

1) Функция вида , где т ≥ 0 – целое число, а₀, а₁, ..., а_m – любые числа, называемые коэф­фициентами (а₀ ≠ 0), называется целой рациональной функцией или алгебраическим многочленом степени т. Многочлен первой степени называется также линейной функцией.

2) Функция, представляющая собой отношение двух целых рациональных функций , называется дробно-рациональной функцией. Совокупность целых рациональных и дробно-рациональных функций образует класс рациональных функций.

3) Функция, полученная с помощью конечного числа супер­позиций и четырех арифметических действий над степенными функ­циями как с целыми, так и с дробными показателями и не являю­щаяся рациональной, называется иррациональной функцией. Например,

и т. д. – иррациональные функции.

4) Всякая функция, не являющаяся рациональной или ирра­циональной, называется трансцендентной функцией. Это, напри­мер, функции f (х) = sin х, f (х) = sin х+ х и т.д.

6.2. Предел функции

1. Предел функции при х→х₀. Пусть функция f(х) опреде­лена на некотором множестве Х и пусть точка х₀  X или х₀  X. Возьмем из Х последовательность точек, отличных от х₀:

x₁, х₂, х₃, …, х_n , …, (1)

сходящуюся к х₀ (предполагается, что такая последовательность существует). Значения функции в точках этой последователь­ности также образуют числовую последовательность

f(х₁), f(х₂), f(х₃), ..., f(x_n), ..., (2)

и можно ставить вопрос о существовании ее предела.

Определение 1. Число А называется пределом функции f(x) в точке х = х₀ (или при х→ х₀), если для любой сходящейся к х₀ последовательности (1) значений аргумента х, отличных от х₀ , соответствующая последовательность (2) значений функции схо­дится к числу А.

Символически это записывается так: .

Функция f (х) может иметь в точке х₀ только один предел. Это следует из того, что последовательность имеет только один предел.

Р а с с м о т р и м п р и м е р ы.

1. Функция f(x)= C = const имеет предел в каждой точке х₀ числовой прямой. В самом деле, если (1) – любая последовательность, сходящаяся к х₀ , то последовательность (2) имеет вид С, …, С, ..., С, ..., т.е. f(х_n) = С. Отсюда заключаем, что f(х_n) → С при n → ∞ или .

2. Функция f(x) = x имеет в любой точке х₀ числовой прямой предел, равный х₀. В этом случае последовательности (1) и (2) тождественны, т.е. f(х_n) = x_n. Следовательно, если х_n → х₀ , то f(х_n) → х₀ при п → ∞ или .

3. Функция f(x) = sin (1/х) (рис. 42), определенная для всех х ≠ 0, в точке х = 0 не имеет предела. Действительно, возьмем две последовательности значений аргумента х: 1/π , 1/(2 π), 1/(3 π), ..., 1/(п π), ... и 2/ π, 2/(5 π), 2/(9 π) ..., 2/[(4п3)π], ... сходящиеся к нулю. Для них соответствующими последователь­ностями значений функции являются:

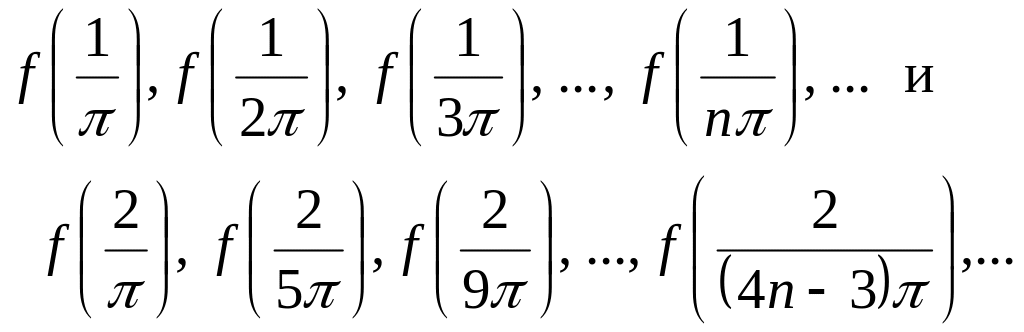Так как при любом п

,

т о для первой последовательности , а для второй последовательности .

Рис. 42

Таким образом, для двух сходящихся к нулю последовательно­стей значений аргумента х соответствующие последова­тельности значений функции имеют разные пределы. А это по определению предела фун­кции и означает, что не существует.

(29)

4. Функция имеет в точке х = 0 предел, равный 1. Действительно, возьмем любую последовательность значений аргумента х, сходя­щуюся к нулю, т. е. , и х_п ≠ 0, тогда имеем

Таким образом, существует , и так как он не зависит от выбора последовательности {х_п}, сходящейся к нулю, то на основании определения предела функции заключаем, что

(29)

5. Функция Дирихле, значения которой в рациональных точ­ках равны единице, а в иррациональных  нулю, не имеет предела ни в одной точке х₀ числовой прямой. Действительно, для сходя­щейся к точке х₀ последовательности рациональных значений ар­гумента предел соответствующей последовательности значений функции равен единице, а для сходящейся к точке х₀ последовательности иррациональных значений аргумента предел соответствующей последовательности значении функции равен нулю.

Существует другое определение предела функции.

Определение 2. Число А называется пределом функции f (х) в точке х = х₀ , если для любого числа ε > 0 существует число δ > 0 такое, что для всех х X, х ≠ х₀ , удовлетворяющих неравенству , выполняется неравенство .

Используя логические символы, определение 2 можно записать в виде

Отметим, что неравенства х ≠ х₀, |x  x₀| < δ можно записать в виде 0 < |x  x₀| < δ .

Первое определение основано на понятии предела числовой последовательности, поэтому его часто называют определением «на языке последовательностей». Второе определение называют определением «на языке ε – δ».

Теорема 1. Первое и второе определения предела функции эквивалентны.

2. Предел функции при х → х₀ – и при х → х₀ +. В дальнейшем будут использованы понятия односторонних пределов функции, которые определяются следующим образом.

Определение 3. Число А называется правым (левым) пределом функции f(x) в точке х₀ , если для любой сходящейся к х₀ последовательности (1), элементы х_п которой больше (меньше) х₀ , соответствующая последовательность (2) сходится к А.

Символическая запись:

.

В качестве примера рассмотрим функцию

f(x) = sign x =

Она имеет в точке х = 0 правый и левый пределы:

В самом деле, если (1) – любая сходящаяся к нулю последовательность значений аргумента этой функции, элементы х_п которой больше нуля (х_п > 0), то sign x_n = 1 и . Следовательно, . Аналогично устанавливается, что .

Можно дать равносильное определение односторонних пределов функции «на языке ε – δ»: число А называется правым (левым) пределом функции f(х) в точке х₀ , если для любого ε > 0 существует δ > 0 такое, что для всех х, удовлетворяющих неравенствам х₀ < x < x₀ + δ (x₀ – δ < x < x₀), выполняется неравенcтво | f(x)  A | < ε. Символическая запись:

Связь между односторонними пределами и пределом функции устанавливает следующая теорема.

Теорема 2. Функция f(x) имеет в точке х₀ предел только тогда, когда в этой точке существуют как правый, так и левый пределы, и они равны. В этом случае предел функции равен односторонним пределам.

3. Предел функции при х→ ∞, при х→  ∞ и при х→ + ∞. Кроме рассмотренных понятий предела функции при х→ х₀ и односторонних пределов существует также понятие предела функции при стремлении аргумента к бесконечности.

Определение 4. Число А называется пределом функции f(х) при х → ∞, если для любой бесконечно большой последовательности (1) значений аргумента соответствующая последовательность (2) значений функции сходится к А.

Символическая запись: .

Определение 5. Число А называется пределом функции f(х) при х → + ∞ ( х→ ∞), если для любой бесконечно большой последовательности значений аргумента, элементы x_n которой положительны (отрицательны), соответствующая последовательность значений функции сходится к А.

Символическая запись:

Р а с с м о т р и м п р и м е р. Пусть f(x) = . Эта функция имеет предел, при х→ ∞ равный нулю. Действительно, если  бесконечно большая последовательность значений аргумента, то соответствующая последовательность значений функции: является бесконечно малой и поэтому имеет предел, равный нулю, т.е. .

Определения 4  5 даны «на языке последовательностей». Можно дать равносильные определения «на языке   » и записать их с помощью логических символов. В качестве примера сформулируем определение предела функции при х  +.

Определение 6. Число А называется пределом функции f(x) при х+, если для любого числа  > 0 существует число  > 0 такое, что для всех хХ, удовлетворяющих неравенству х > , выполняется неравенство | f(x)  A| < .