Литература

1. Крючков А. П. Общая технология СК. – М.: Химия, 1965. 526 с.

2. Рейсхфельд В. О., Еркова Л. Н. Оборудование производств основного органического синтеза и синтетических каучуков. – Л.: Химия, 1974. 437 с.

3. Герман Х. Шнековые машины в технологии. – М.: Химия, 1975. 684 с.

4. Бекин Н. Г. Оборудование и основы проектирования заводов резиновой промышленности. – М.: Химия, 1985. 542 с.

5. Шейн В. С. Процесс выделения и обезвоживания синтетических каучуков.– М.: Химия, 1970, 738 с.

6. Рябинин О. П. Расчёт и конструирование оборудования химической промышленности. – Л.: Химия, 1954. 680 с.

7. Вострокнутов Е. Г. Переработка каучуков и резиновых смесей. – М.: Химия, 1975. 529 с.

8. Берхард Э. Переработка термопластичных материалов. – М.: Химия, 1962. 747 с.

9. Берд Р., Стюарт В., Лайтфут Е. Явления переноса. – М.: Химия, 1974. 689 с.

Приложение 8. О гидродинамическом равновесии шарика в изогнутой трубке

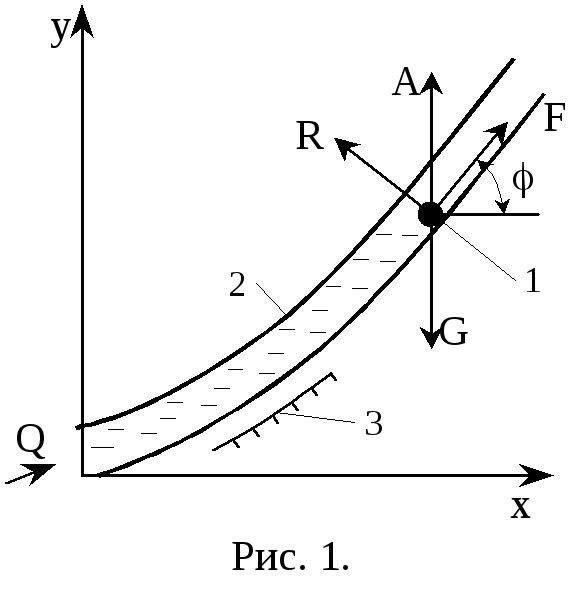Рассмотрена задача статического равновесия тяжелого шарика в изогнутой трубке постоянного диаметра при протекании в ней с постоянным расходом жидкости или газа. Схема течения и система координат представлены на рис.1. Шарик 1 диаметром d помещен в трубку 2 внутренним диаметром D. Для контроля положения шарика в прозрачной трубке служит шкала 3. Слева в трубку подается жидкость (газ) с постоянным расходом Q. Ось декартовой системы координат x направлена горизонтально, ось y - вертикально. Ось трубки s лежит в вертикальной плоскости. Угол φ характеризует наклон касательной к траектории трубки в точке ее касания шариком. На шарик действуют силы: G - собственного веса, А - архимедова сила, R - реакция от стенки трубки (направлена по нормали к оси трубки), F - сила динамического воздействия протекающего потока жидкости.

В положении равновесия сумма всех сил, действующих на шарик (равнодействующая которых проходит через его центр тяжести), равна нулю.

Проекции сил на оси x и y имеют вид:

-R cos(π/2-φ)+F cos φ = 0, A - G + F sin φ + R sin (π /2 - φ) = 0.

Исключив из этих уравнений R, получим соотношение

F = (G - A) sin φ. (1)

Найдем силы, входящие в (1). Для собственного веса и архимедовой силы можно записать

G - A = g (ρ_т - ρ)πd³/6, (2)

где ρ_т, ρ - плотности материала шарика и среды, g – ускорение свободного падения.

Рассматривая шарик как местное сопротивление, можно определить силу динамического воздействия среды так:

F = 0,25πd²ΔP, (3)

где ΔP - падение давления на шарике. Падение давления в местном сопротивлении найдем по известной формуле [1]

ΔP = 0,5ξ ρ v² , (4)

где ξ =25,2/Re+(1/e+n)² - коэффициент местного сопротивления как для ламинарного, так и для турбулентного режимов; n = 1-(d/D)²; e=0,57+ 0,043/(1,1-n); Re=v_e(D-d)ρ/μ – число Рейнольдса для серповидного зазора между шариком и стенкой трубки; v_e =4Q/[π(D²-d²)] - средняя скорость в узком сечении.

Из совместного рассмотрения (1)-(4) следует уравнение, связывающее расход среды и локальный угол наклона трубки

bQ² + aQ - sin φ = 0, (5)

где a =75,6μ(D+d)/[πgd(ρ_т-ρ)(D²-d²)²], b =12 ρ(1+ne) ²/[π²gde²(ρ_т-ρ)(D²-d²)²].

Отметим, что уравнение (5) описывает равновесие шарика при любом режиме течения жидкости. Разрешая уравнение (5) относительно расхода, получим

Q = 2 sin φ /[a + ]. (6)

Из формулы (6) видно, что соотношение коэффициентов a и b определяет режим течения.

Пусть угол наклона трубки монотонно возрастает по ее длине. Предельным углом для конца трубки является φ = π/2. При этом реакция от стенки R уменьшается до нуля, шарик свободно "витает" в поперечном сечении и скорость потока равна скорости уноса шарика. Этот режим характеризует максимально возможный расход среды Q_m. Изогнутая трубка, выполненная из прозрачного материала, у которой угол наклона касательной к оси плавно возрастает от φ = 0 до φ = π/2, позволяет по положению шарика, контролируемому посредством шкалы, измерять расход протекающей среды.

Для определения максимально допустимого расхода Q_m достаточно в (6) положить φ = π/2. Имеем

Q_m = 2/[a + ]. (7)

Гидродинамический режим может быть охарактеризован одним безразмерным параметром - числом Архимеда. Модифицированное для данной задачи число Архимеда определяется выражением

Ar = .

Соответственно, для максимального расхода можем записать

Q_m =2/[a(1 +)].

Из выражения для Ar видно, что ламинарный режим имеет место при малых D, (ρ_т - ρ) и больших μ.

Численный анализ (7) показал, что Q_m в основном определяется внутренним диаметром трубки D и соотношением физических свойств ρ, μ, (ρ_т - ρ). Увеличение диаметра шарика в пределах от d/D=0,07 до 0,5 повышает Q_m в среднем в 1,5-2 раза. Дальнейшее увеличение d/D приводит к снижению Q_m. Следует отметить, что при больших отношениях d/D возрастает гидравлическое сопротивление устройства. Режим течения по преимуществу турбулентный.

Рассмотрим случай ламинарного режима течения, для которого правомерны соотношения a²>>b, b≈0. Полагая в (5) b=0, имеем

= sin φ. (8)

Согласно (8) угол динамического равновесия (соответственно и положение шарика в изогнутой трубке) зависит не только от расхода Q, но и от вязкости. Следовательно, организовав в трубке течение с постоянным расходом Q=const, можно непрерывно контролировать вязкость протекающей среды по положению шарика. При значительной длине трубки и незначительном изменении угла наклона, что ограничено трением качения шарика по стенке трубки, можно получить достаточно высокую точность измерения вязкости или контролировать малое ее отклонение.

Зависимость Q_m от d/D носит экстремальный характер. Найдем координату точки максимума. Запишем выражение (7) в форме

Q_m=,

где H=d/D. Продифференцировав это выражение по H и приравняв нулю, получим кубическое уравнение 4H³+5H²-1=0. Действительный положительный корень этого уравнения H=d/D=(-1)/8=0,3903882. Шарик с таким диаметром, при прочих равных условиях, наименее отклоняется под действием потока жидкости. Этому значению H соответствует максимальный расход жидкости

Q_m = .

Численный анализ показывает, что и в турбулентном режиме Q_m также имеет экстремум (в окрестности d/D≈0,5), но найти его возможно только численно.

Наибольшую точность измерения можно получить в случае линейной или равномерной шкалы отсчета положения шарика. Поэтому найдем конфигурацию трубки, обеспечивающую равномерную шкалу. Равномерность шкалы обеспечивается при линейной зависимости длины участка трубки от начального сечения до сечения, где находится шарик от расхода Q (Q<Q_m). Математически это условие формулируется следующим образом s=KQ, или учитывая (6), можем записать

s = 2K sin φ /[a + ], (9)

где К - коэффициент пропорциональности.

Для плоской кривой характерны следующие геометрические соотношения:

ds/dx = 1 + y'², y' = dy/dx = tg φ. (10)

Пусть общая длина трубки s_o (s_o>>D). Тогда, с учетом условия для верхнего конца трубки s=s_o, при φ =π/2, найдем, используя (9), коэффициент К. Имеем К= s_o(a+)/2. Подставив К в (9), получим уравнение

s = s_o(a+) sin φ /[a + ]. (11)

Уравнения (10), (11) в параметрической форме x(s),y(s) описывают траекторию трубки с равномерной шкалой отсчета. Граничные условия задачи

x=0, y=0, s=0, φ =0; x=x_o, y=y_o, s=s_o, φ =π/2. (12)

Параметры x_o, y_o, s_o, характеризуют размерные координаты верхнего конца трубки и ее общую длину. Причем параметры x_o, y_o неизвестны, а длина s_o задана.

Для дальнейшего анализа задачи ее удобно записать в безразмерной форме

dX/dS = cosφ , dY/dS = sinφ,

S=0, X=0, Y=0, φ =0; S=1, X=X_o, Y= Y_o, φ =π/2, (13)

где X=x/s_o, Y=y/s_o, S=s/s_o, B²=1+4Ar sinφ. При решении задачи (13) методом Рунге-Кутта удобно выбирать шаг по S, равный шагу отметок шкалы расхода, например, 0,05 или 0,1.

Из (13) видно, что форма трубки в общем случае зависит от числа Архимеда, т.е. от режима течения. Следовательно, проектировать ротаметр можно только под конкретную среду и размеры шарика и трубки. В противном случае шкала будет неравномерной. В общем случае система (13) не имеет аналитического решения, поэтому рассмотрим частные случаи.

Ламинарный режим течения. При Ar решение задачи (13) имеет вид

X= 0,5φ + 0,25 sin 2φ, Y=0,5 sin²φ, S= sinφ (14)

Безразмерные координаты верхнего конца трубки: φ =π/2, X= π/4, Y=1/2, S=1. Траектория трубки, расcчитанная по (14), с отметками шкалы, показана на рис. 2 (линия 1). Шаг по S был взят 0,1.

Другой предельный случай - турбулентный режим течения. При Ar>>1 уравнения (13) частично интегрируются. Имеем

X= , Y=S/3, S= .

Для функции X решение можно представить, используя эллиптический интеграл первого рода [2]

X=( 2/3)[F(90^o,45^o) - F(arcos S,45^o)] - (S/3) ,

где F(90^o,45^o) = 1,85407468. Координату верхнего конца трубки определим, используя равенство F(0,45^o)=0. Имеем: X=0,8740191, Y=1/3, S=1, φ =π /2.

Расчетная шкала показана на рис. 2 (линия 2). Из рисунка видно, что в турбулентном режиме начальный участок шкалы (Х<0,3), имеющий слабый наклон, мало пригоден для измерений, т.к. трудно обеспечить высокую точность изготовления трубки и обеспечить минимальное трение качения. Следует отметить, что минимальное трение качения имеет место при высокой твердости соприкасающихся поверхностей, т.е. материалов шарика и стенки трубки (например, пара сталь-стекло).

Рис. 2.

Очевидно, что в промежуточных режимах течения (средних значениях числа Архимеда) конфигурация трубки будет занимать среднее положение между линиями, представленными на рис. 2.

Согласно [3] искривленность трубки увеличивает ее гидравлическое сопротивление. Кроме того, в искривленной трубке максимум скорости смещается к внешней стенке, где именно находится шарик. Поэтому проведенный анализ можно рассматривать как инженерную оценку задачи.

ЛИТЕРАТУРА

1. Альтшуль А.Д. Гидравлические сопротивления. -М.: Недра, 1982.-С.224.

2. Прудников А.П., Брычков Ю.А., Маричев О.И. Интегралы и ряды.-М.: Наука, 1981.-800С.

3. Шлихтинг Г. Теория пограничного слоя. -М.: Наука, 1969.-744С.

Шаповалов Владимир Михайлович

ВОЛЖСКИЕ ТЕХНОЛОГИЧЕСКИЕ МАШИНЫ

Математическое моделирование процессов переноса

Учебное пособие

Редактор Е.М. Марносова

Темплан 2003., поз. №____

Лицензия ИД №04790 от 18.05.2001.

Подписано в печать __________. Формат 60х84 1/16

Бумага газетная. Печать офсетная. Усл. Печ.л. 5,58

Уч.-изд.л.2,79. Тираж 200 экз. Заказ _______.

Волгоградский государственный технический университет.