-
Нестационарная теплопроводность шара при граничных условиях 3-го рода
Музыка – скрытое арифметическое упражнение души,
не умеющей себя вычислить.
Лейбниц
В
технологии переработки полимеров часто
встречается технологическая операция,
связанная с прогревом или охлаждением
изделий, имеющих форму, близкую к форме
шара. Например, вулканизация резиновых
изделий (имеет место прогрев материала),
охлаждение в литьевой форме изделий из
термопластов после формования. Во всех
указанных случаях, а также в ряде других
имеет место нестационарная теплопроводность
тела шарообразной формы. Задачей является
определение необходимого времени для
достижения внутренней точкой изделия
нужной температуры. Поскольку именно
это время определяет продолжительность
технологического процесса, а следовательно
и производительность оборудования.
Считаем
задачу осесимметричной (
).
Расчетная схема представлена на рис.
2.6.
Уравнение энергии, описывающее нестационарное поле в шаре, имеет вид
,
t=0; T=T0,
r=0;
,
r=R,
-
,
где а – коэффициент температуропроводности, То- начальная температура материала шара, Тс – температура окружающей среды.
Введем безразмерные переменные и параметры
x=
;
F0=
;
;
Bi=
.
Тогда задача примет форму
,
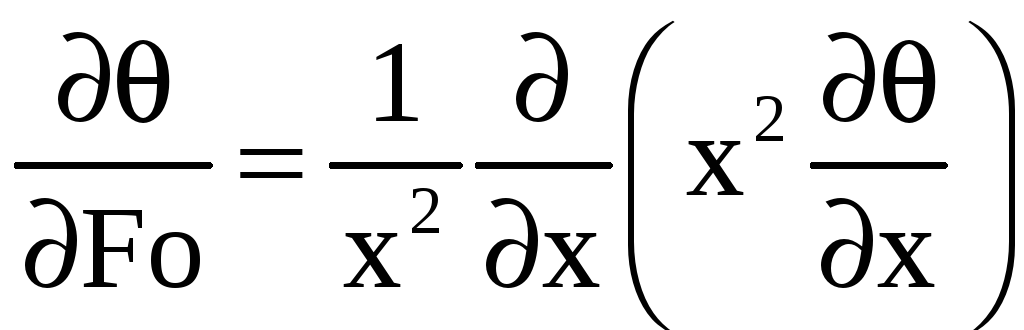F0=0;
,
x=0;
,
x=1;
.
Приближенное решение ищем в формуле
.
Элемент объема в сферических координатах
dV=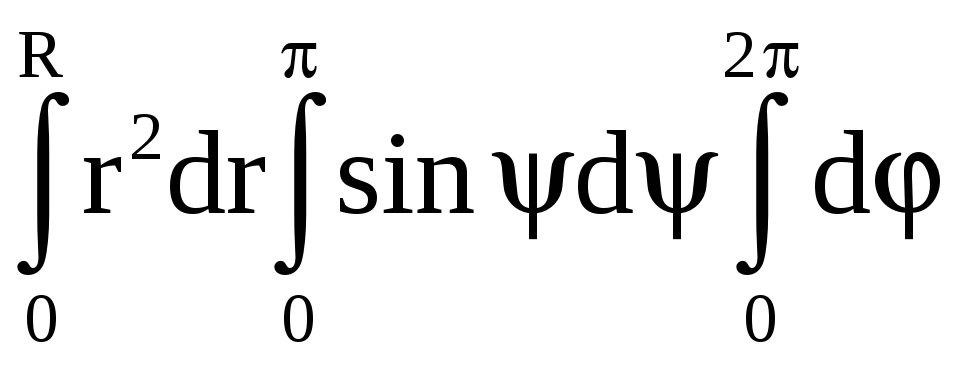
.
Следовательно, условие ортогональности имеет вид
Невязка уравнения энергии для заданного температурного поля имеет вид
.
В развернутой форме условие ортогональности имеет вид
.
Раскроим скобки в подынтегральном выражении
.
После выполнения интегрирования, получим дифференциальное уравнение первого порядка для неизвестной функции а
.
Разделим переменные и проинтегрируем с учетом начального условия
В результате получим выражение для функции а
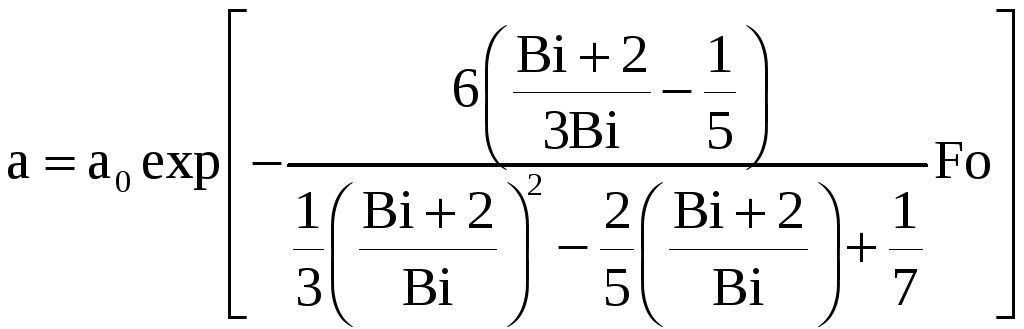
Для определения постоянной ао используем интегральное условие
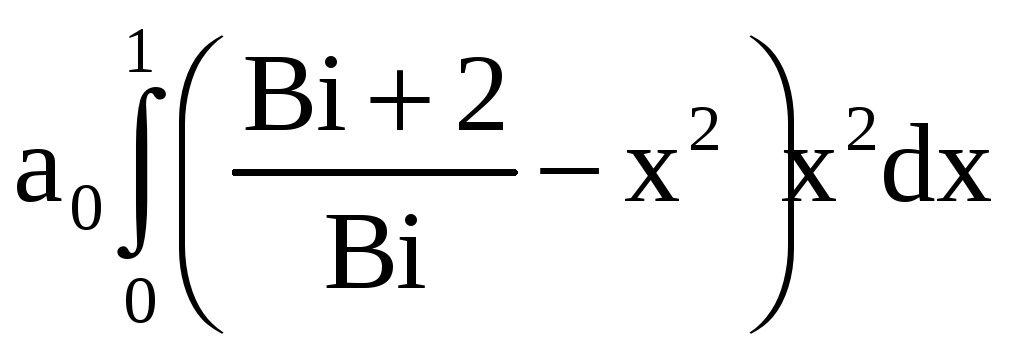
=1.
Выполнив интегрирование, получим
.
Таким образом, имеем следующее выражение для расчета безразмерной температуры любой точки внутри шара
.
В случае высокой интенсивности теплообмена (Bi>>1) можно считать на поверхности шара граничное условие первого рода. В этом случае расчетное выражение для температуры существенно упрощается
.
Наиболее медленно изменяется температура внутренней точки шара, находящейся в центре, т.е. имеющая координату х=0. Температура в центре шара
.
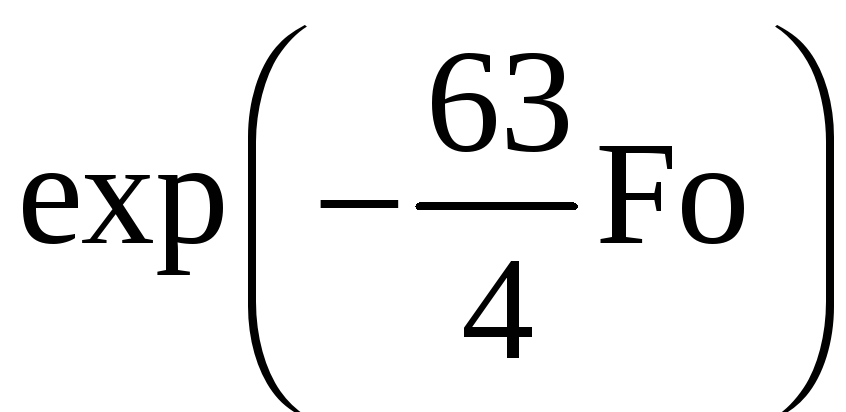