2.2. Диссипативный саморазогрев при напорном течении

вязкой жидкости в плоской щели

Обопри на себя лишь посильное.

Пиндар

И докажи, пожертвовав собой,

Что человек богам не уступает.

Гете

При транспортировке высоковязкой жидкости происходит повышение ее температуры за счет перехода механической энергии в тепло. Т.е. температура жидкости постоянно повышается. Отвод тепла от жидкости осуществляется по механизму радиальной теплопроводности к стенкам трубы.

На определенном удалении от входа температурное поле в жидкости стабилизируется (см. рис. 2.2). Этот вид течения имеет место, например, при впрыске пластифицированной резиновой смеси (10⁵ Пас) в форму, а именно – течение в узких каналах пресс-формы. Также это течение имеет место при литье полимеров. Но что касается резиновой смеси, то здесь есть опасность подвулканизации ее за счет диссипативного саморазогрева, что отрицательно скажется на качестве изделия. Напомним, что резина является реактопластом.

Рассмотрим упрощенный вариант задачи, когда теплофизические свойства жидкости (, , , с) постоянны.

Известно, что поле скоростей вязкой жидкости в плоском канале описывается параболической зависимостью (см. гл. 1.6.2)

,

где _m-скорость на оси. В условиях ламинарного течения _m=2_ср и Q=F_ср, т.е. _m=2Q/F, где F-площадь сечения канала (F=2hB), B – ширина канала.

Уравнение Фурье – Кирхгофа, с учетом одномерности и стационарности теплового потока (), имеет вид

.

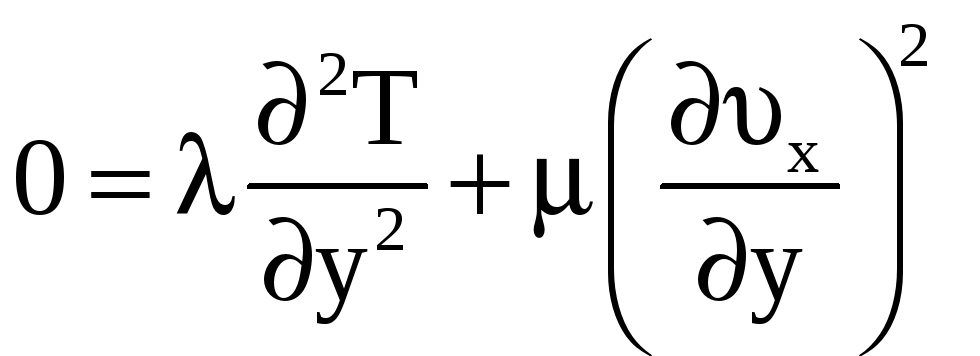Второе слагаемое в этом уравнении характеризует диссипативное тепловыделение.

С учетом производной от осевой скорости

,

уравнение теплопроводности примет вид

.

Проинтегрируем это уравнение по y

.

Повторное интегрирование дает

.

Постоянные интегрирования найдем, используя граничные условия для температуры. Принимаем граничные условия 1-го рода, т.е. стенки изотермические y=h, T = T_c. Из условия температурной симметрии задачи следует y=0, . Поэтому с₁=0, а для с₂ имеем

,

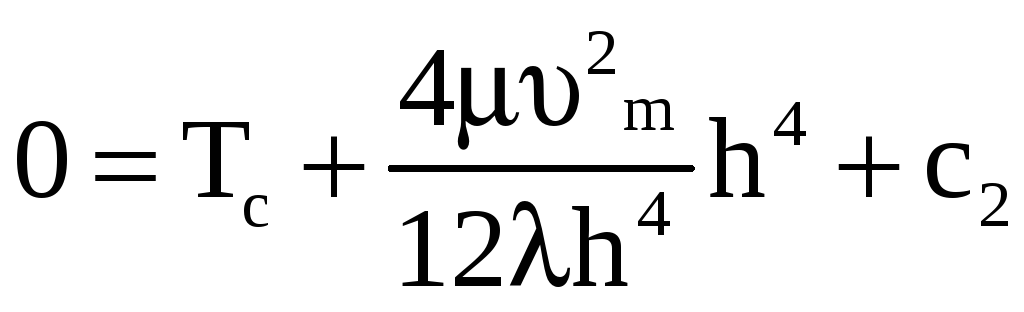Откуда

.

Подставим с₂ в выражение для температуры

.

Из полученного выражения видно, что распределение температуры описывается параболой четвертой степени.

Максимальное повышение температуры жидкости имеет место на оси канала

.

Из выражения видно, что повышение температуры на оси канала (последнее слагаемое) не зависит от высоты канала, но определяется вязкостью жидкости, ее теплопроводностью и квадратом скорости жидкости на оси.

Пример.

Имеется плоский участок литьевой системы при формовании резины. Эффективная вязкость резины 10⁴ Па.с. Теплопроводность резины 0,14 Вт/мК. Средняя скорость течения 0,02 м/с. Определить диссипативное повышение температуры.

Решение.

Используем формулу для температуры в середине щели

.

Известно, что максимальная скорость жидкости на оси в два раза больше средней. Можем записать

.

Имеем существенное повышение температуры, поэтому есть опасность подвулканизации резиновой смеси.

Задачи.

1. Если в условиях рассмотренного примера сохраняя расход жидкости, уменьшить высоту щели. Как изменится саморазогрев?

2. Сформулировать краевую задачу в случае течения степенной жидкости.