
- •ПРЕДИСЛОВИЕ
- •Глава 1. МАТЕМАТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
- •Лабораторная работа № 1
- •Лабораторная работа № 2
- •Лабораторная работа №3
- •Цель работы
- •Содержание работы
- •Описание лабораторной установки
- •Методика эксперимента
- •Порядок выполнения работы
- •Обработка результатов измерений
- •Высота
- •подъема
- •груза
- •Контрольные вопросы
- •Лабораторная работа № 5
- •Лабораторная работа № 6
- •Таблица 4.15
- •Обработка результатов прямых измерений
- •Результаты вычислений
- •Таблица 5.2
- •Параметры лабораторной установки
- •Таблица 5.3
- •Результаты эксперимента и обработки результатов
- •Стальной брус
- •Латунный брус
- •6.1. Гармонические колебания
- •6.2 Затухающие колебания
- •6.3 Вынужденные колебания
- •Лабораторная работа № 9
- •Цель работы
- •Содержание работы
- •Описание лабораторной установки
- •Методика эксперимента
- •Порядок выполнения работы
- •Обработка результатов измерений
- •Контрольные вопросы
- •Лабораторная работа № 10
- •Цель работы
- •Содержание работы
- •Описание лабораторной установки
- •Методика эксперимента
- •Порядок выполнения работы
- •Обработка результатов измерений
- •Контрольные вопросы
- •Лабораторная работа №11
- •Цель работы
- •Описание лабораторной установки
- •Содержание работы
- •Методика эксперимента
- •Порядок выполнения работы
- •Определение периода собственных колебаний маятника
- •Изучение вынужденных колебаний маятника
- •Обработка результатов измерений
- •Контрольные вопросы
- •Цель работы
- •Содержание работы
- •Описание лабораторной установки
- •Методика проведения эксперимента
- •Порядок выполнения работы
- •Обработка результатов измерений
- •Контрольные вопросы
- •Цель работы
- •Содержание работы
- •Описание моделирующей программы
- •Порядок выполнения работы
- •Анализ результатов моделирования
- •Контрольные вопросы
- •ГЛАВА 7. ВОЛНОВОЕ ДВИЖЕНИЕ
- •Методика эксперимента и описание установки
- •Контрольные вопросы
- •Описание лабораторной установки
- •Обработка результатов измерений
- •Контрольные вопросы
- •Лабораторная работа №18
- •Цель работы
- •Содержание работы
- •Методика проведения численного эксперимента на ЭВМ
- •Порядок выполнения работы
- •Завершение работы
- •Обработка результатов измерений
- •Контрольные вопросы
- •Лабораторная работа №19
- •Методика эксперимента
- •Порядок выполнения работы
- •Обработка результатов измерений
- •Контрольные вопросы
- •Таблица 9.1
- •Таблица 9.2
- •Таблица 9.3
- •Глава 10. ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ
- •10.1. Поведение молекул в приповерхностном слое жидкости
- •10.2. Коэффициент поверхностного натяжения
- •10.3. Давление под изогнутой поверхностью жидкости
- •10.4. Краевой угол
- •Добавочное давление под изогнутой поверхностью
- •Поэтому высота жидкости в капилляре равна
- •Лабораторная работа № 22
- •Цель работы
- •Содержание работы
- •Порядок выполнения работы
- •Обработка результатов измерения
- •Контрольные вопросы
- •ОГЛАВЛЕНИЕ

6.2 Затухающие колебания
Ранее упоминалось, что во всех реальных колебательных системах действуют силы сопротивления (трения), приводящие к рассеянию энергии и затуханию колебаний. Выражение для такой силы сопротивления имеет вид
FC = −rυ . |
(6.29) |
Знак «минус» указывает на то, что сила направлена против направления движения тела.
В случае груза на пружине проекция силы сопротивления на ось OX определяется выражением
F = −r |
dx |
, |
(6.30а) |
C dt
а для математического и физического маятников необходимо учитывать проекцию момента сил сопротивления на ось вращения (например, вязкое трение среды или трение в оси вращения)
M C = −r |
dϕ |
. |
(6.30б) |
|
|||
|
dt |
|
|
Здесь r – коэффициент сопротивления среды. |
|
||
Для примера рассмотрим случай наличия силы трения в оси вращения физического маятника. Для этого запишем уравнение динамики вращательного движения (6.14) с учетом (6.21) и (6.30,б)
|
|
J d 2ϕ |
= −mgl sinϕ − r dϕ . |
(6.31) |
||
|
r |
dt 2 |
mg |
dt |
|
|
Вводя обозначение β = |
, ω0 = |
и рассматривая случай малых уг- |
||||
2J |
J |
|||||
|
|
|
|
|||
лов, когда sinϕ ≈ ϕ , получим (в случае груза на пружине легко получить подобное уравнение, только относительно переменной х):
d 2ϕ |
+ 2β dϕ |
+ ω02ϕ = 0 . |
(6.32) |
dt 2 |
dt |
|
|
В случае, когда ωo > β, решением этого уравнения будет следующая зависимость угла отклонения маятника от времени:
ϕ = A e−β t |
cos(ωt +α |
0 |
), |
(6.33) |
0 |
|
|
|
|
где β – коэффициент затухания; ω = |
ω02 − β 2 |
|
– |
собственная круговая |
частота затухающих колебаний. Необходимо отметить, что величина собственной круговой частоты отлична от круговой частоты собственных незатухающих колебаний – сравните полученные результаты с (6.24).
Как следует из вида функции (6.33), данные колебания не являются гармоническими, так как зависимость угла отклонения маятника от времени не является только функцией косинуса или синуса. Период затухающих
101

колебаний (промежуток времени между двумя соседними максимумами колебания) равен:
T = |
2π |
|
ω2 − β 2 . |
(6.34) |
|
|
0 |
|
На (рис. 6.5) приведен график функции (6.33), на котором видно, что |
||
амплитуда колебаний со временем убывает по закону A(t) = A e−β t . Время |
||
|
|
0 |
τ, за которое амплитуда затухающих колебаний уменьшится в е раз, назы- |
||||||||||
вают временем релаксации. Его можно найти из соотношения |
A(t) |
|||||||||
|
= e , |
|||||||||
A(t +τ ) |
||||||||||
|
A e−β t |
|
βτ |
|
βτ |
|
|
|
|
|
откуда следует |
0 |
= e |
|
и e |
|
= e , окончательно получаем βτ =1. |
||||
A e−β(t+τ ) |
|
|
||||||||
|
0 |
|
|
|
|
То есть, время релаксации есть вели- |
||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
чина, обратная коэффициенту зату- |
||||
|
|
|
|
|
|
хания |
|
|
||
|
|
|
|
|
|
τ = |
1 |
. |
(6.35) |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
β |
|
|
|
|
|
|
|
|
|
Формула (6.35) показывает, что |
||||
|
|
|
|
|
|
коэффициент затухания β характе- |
||||
|
|
|
|
|
|
ризует уменьшение амплитуды коле- |
||||
|
|
|
|
|
|
баний за единицу времени. |
||||
Рис. 6.5 |
|
|
|
|
Так же часто используется еще |
|||||
|
|
|
|
|
|
одна характеристика затухания коле- |
||||
баний, которая называется логарифмическим декрементом затухания. Логарифмический декремент затухания равен натуральному лога-
рифму отношения амплитуды колебаний в данный момент времени к ам-
плитуде через период: |
|
|
A(t) |
|
|
||||
|
|
|
|
|
|||||
δ = ln |
|
|
|
|
. |
|
(6.36) |
||
A(t +T ) |
|
||||||||
Подставим сюда закон изменения амплитуды со временем |
|||||||||
|
A e−β t |
β T |
, |
||||||
δ = ln |
0 |
|
|
|
= ln e |
|
|||
A e−β |
(t +T ) |
|
|||||||
|
0 |
|
|
|
|
|
|
|
|
|
δ = β Т . |
|
(6.37) |
||||||
С учетом выражения (6.35) получим |
|
|
|
|
|
|
|
||
|
δ = T |
= |
1 |
, |
|
|
(6.38) |
||
|
|
|
|
||||||
|
τ |
|
Ne |
|
|
||||
где Ne = τ /T – число колебаний, после совершения которых амплитуда колебаний уменьшается в е раз.
102
Выражение (6.38) показывает, что логарифмический декремент характеризует уменьшение амплитуды колебаний за один период.
В инженерных расчетах и технических характеристиках колебательных систем для описания затухания часто используют понятие добротности. Добротность определяется выражением
Q = |
π |
= |
1 |
= πNe . |
(6.39) |
|
δ |
β T |
|||||
|
|
|
|
Физический смысл добротности будет раскрыт позже, при рассмотрении вынужденных колебаний.
Из уравнения (6.34) видно, что при значениях β = ω0 величина периода
затухающих колебания обращается в бесконечность. То есть система, выведенная из равновесия и предоставленная сама себе, бесконечно долго возвращается в положение равновесия. В случаеβ ≥ω0 из решения уравне-
ния (6.32) получают, что движение системы перестает быть периодическим
– становится апериодическим, то есть экспоненциально стремится к положению равновесия без совершения колебательных движений.
6.3 Вынужденные колебания
Рассмотрим вынужденные колебания. В этом случае к возвращающей силе и силе сопротивления необходимо добавить внешнюю периодическую силу (момент силы). Момент внешней периодической силы запишем в виде:
M ВН = M 0 cos(Ωt ), |
(6.40) |
где Ω – циклическая частота внешней силы.
Тогда уравнение динамики вращательного движения (6.14) с учетом
(6.21), (6.30,б) и (6.40) примет вид:
|
|
J d 2ϕ = −mgl sin(ϕ)− r dϕ |
+ M |
0 |
cos(Ωt), |
|
(6.41) |
||||||||
|
|
dt 2 |
|
|
dt |
|
|
|
|
|
|
||||
при |
малых углах отклонения, |
вводя обозначения β = |
r |
, ω0 = |
mg |
и |
|||||||||
2J |
J |
||||||||||||||
|
M 0 |
|
|
|
|
|
|
|
|
|
|
|
|||
µ0 = |
перепишем (6.41) в виде: |
|
|
|
|
|
|
|
|
||||||
J |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
d 2ϕ |
+ 2β |
dϕ |
+ω02ϕ = µ0 cos(Ωt). |
|
|
(6.42) |
||||||
|
|
|
|
dt |
|
|
|||||||||
|
|
|
dt 2 |
|
|
|
|
|
|
|
|
|
|||
Это неоднородное дифференциальное уравнение второго порядка для вынужденных колебаний математического маятника. Его решение есть сумма общего решения однородного уравнения и частного решения неоднородного. Общее решение описывает переходный процесс возбуждения колебаний, а частное – установившиеся вынужденные колебания вида
ϕ(t) = Acos(Ωt +α) .
По истечении некоторого времени в установившемся режиме вынужденные колебания маятника будут происходить с частотой Ω внешнего
103

воздействия, а амплитуда и начальная фаза колебаний будут определяться параметрами самого маятника и внешнего периодически изменяющегося момента сил. Амплитуда установившихся колебаний определяется выражением:
A = |
µ0 |
|
; |
(6.43) |
(ω02 − Ω2 )2 |
+ 4β 2Ω2 |
величина фазы α, на которую вынужденные колебания опережают вынуждающую силу следует из уравнения
tgα = |
2βω |
. |
(6.44) |
||
ω2 |
−ω2 |
||||
|
|
|
|||
|
0 |
|
|
|
|
Из формулы (6.43) видно, что амплитуда вынужденных колебаний имеет максимальное значение при некотором значении частоты Ωрез (предполагается, что параметры системы m, l, J, r не изменяются, а меняется частота внешней силы) – эта частота называется резонансной
Ωрез =  ω02 − 2β 2 . (6.45)
ω02 − 2β 2 . (6.45)
Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты внешнего периодического воздействия Ω к собственной частоте ω0 системы – называется резонансом.
Как видно из уравнения (6.43) и (6.45), для возникновения резонанса, совершенно не важно, каким образом происходит «сближение» частот – путем изменения частоты внешнего воздействия Ω, собственной частоты ω0 или коэффициента затухания β.
Найдем величину резонансной амплитуды, для этого подставим (6.45) в (6.43) и получим
Aрез = |
µ0 |
. |
(6.46, а) |
|
ω02 |
||||
2β |
− β 2 |
|
В случае слабых затуханий β << ωo
Aрез = |
µ0 |
. |
(6.46,б) |
|
|||
|
2βω0 |
|
|
В нашем случае Арез представляет собой угол максимального отклонения маятника от положения равновесия.
Рассмотрим случай, когда на систему будет действовать постоянный момент внешней силы
M ВН = M 0 ,
тогда угол отклонения маятника ϕ0, будет называться статическим отклонением. Величину статического отклонения можно определить из следующих соображений:
mglϕ0 = M 0 ,
104
ϕ0 = |
M 0 |
= |
|
M 0 |
|
= |
|
M 0 |
= |
|
|
µ0 |
. |
(6.47) |
|||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
mgl |
|
|
J |
|
|
|
|
|
Jωo2 |
|
ωo2 |
|
||||||
|
|
|
J mgl |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Из (6.46) и (6.47) видно, что Aрез ≈ |
ϕ0ω0 |
= |
ϕ0π |
|
=ϕ0Q , следовательно |
||||||||||||||
2β |
β T |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Q ≈ |
Aрез |
, |
|
|
|
|
|
|
|
|
(6.48) |
||||||
|
|
ϕ0 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
то есть добротность показывает, во сколько раз величина резонансной амплитуды превышает величину статического отклонения.
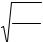
На (рис. 6.4) приведено семейство амплитудных резонансных кривых при различных значениях коэффициента затухания β, на котором также показано, что не всякая система имеет резонансную частоту. Действительно, из (6.45) следует, что Ωрез имеет вещественные значения только при
ω0 ≥  2β , а в остальных случаях резонанс не наблюдается.
2β , а в остальных случаях резонанс не наблюдается.
Рис. 6.6
6.4 Сложение колебаний
Чаще всего в практических задачах приходится рассматривать процессы, в которых изменение физических величин описывается суммой двух или более колебаний, например колебание гитарной струны или человеческий голос. Основные закономерности сложения гармонических колебаний могут быть рассмотрены на примере сложения двух колебаний.
Если тело одновременно участвует в двух колебаниях вдоль оси X x1 (t) = A1 sin (ω1t +ϕ1 ) и x2 (t) = A2 sin (ω2t +ϕ2 ), то его координата x будет описываться уравнением
x(t) = x1 (t) + x2 (t) = A1 sin (ω1t +ϕ1 )+ A2 sin (ω2t +ϕ2 ). |
(6.49) |
105 |
|
|
Например, на тележке стоят часы с ма- |
||||
|
ятником. Координата маятника относительно |
||||
|
тележки |
изменяется |
по |
закону |
|
|
x2 (t) = A2 sin (ω2t +ϕ2 ), а тележку |
качают сона- |
|||
|
правленно с движением маятника так, что ее |
||||
|
координата относительно земли изменяется |
||||
|
по закону |
x1 (t) = A1 sin (ω1t +ϕ1 ). Тогда коорди- |
|||
Рис. 6.7 |
|||||
ната маятника относительно |
земли |
будет |
|||
|
|||||
описываться уравнением (6.49). В этом случае говорят о сложении одина-
ково направленных или параллельных колебаний.
Для наглядного сложения одинаково направленных колебаний удобно использовать метод векторных диаграмм. Рассмотрим два утверждения, на которых базируется метод векторных диаграмм:
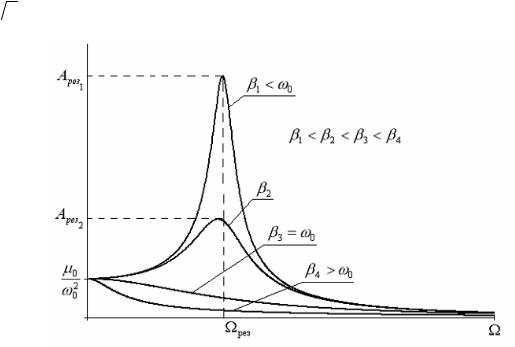
1) Если вектор длины А вращается в плоскости ху в положительном направлении (против часовой стрелки) с угловой скоростью ω, причем в начальный момент времени (t=0) угол между вектором и осью х равен φ, то проекция вектора на ось Ох (рис. 6.7) изменяется со временем по закону
x(t) = Asin (ωt +ϕ). |
(6.50) |
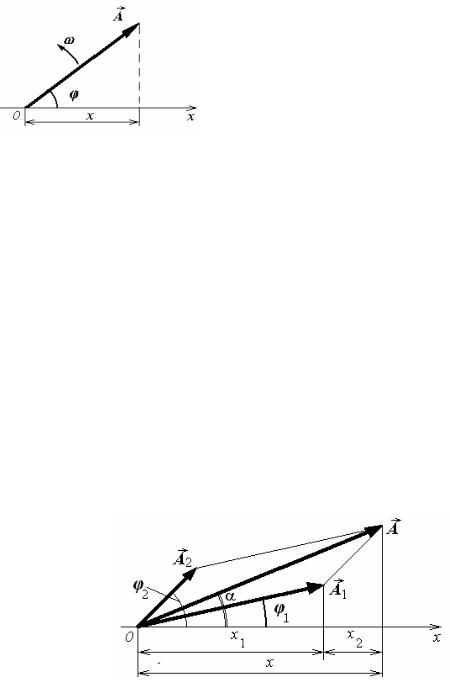
Следовательно, каждому гармоническому колебанию можно сопоставить вектор, вращающийся в плоскости xy. Длина этого вектора будет равна амплитуде колебаний, угловая скорость вращения вектора – циклической частоте колебания, а начальный угол – начальной фазе колебания. 2) Из рисунка (6.8) видно, что проекция суммы векторов на ось равна
сумме проекций этих векторов на ту же ось.
Рис. 6.8
Рассмотрим сложение одинаково направленных гармонических колебаний с одинаковой частотой (амплитуды и начальные фазы могут быть различными или одинаковыми)
x (t)
1
x2 (t)
= A1 sin (ωt +ϕ1 ) |
. |
(6.51) |
|
= A2 sin (ωt +ϕ2 ) |
|||
|
|
Согласно первому утверждению сопоставим колебаниям (6.51) вектора A1 и A2 . Найдем сумму этих векторов A = A1 + A2 и ее проекцию на ось x. Из
106
второго утверждения следует, что проекция суммарного вектора и есть результирующее колебание.
Поскольку длины векторов A1 и A2 , а также угол между ними φ2–φ1 при вращении не изменяются (так как у них одинаковая скорость вращения), то и вектор A будет сохранять неизменной свою длину и расположение относительно векторов A1 и A2 , а значит, A будет вращаться с такой же угловой скоростью, как A1 и A2 . Это отражает тот факт, что сумма двух
гармонических колебаний с одинаковой частотой также является гармоническим колебанием той же частоты.
Наглядность и простота метода векторных диаграмм заключается в том, что основные параметры результирующего колебания можно найти из геометрических соображений. Из рис. 6.8 видно, что амплитуда А и начальная фаза α результирующего колебания определяется следующими выражениями:
A2 = A2 |
+ A2 |
+ 2A A cos(ϕ |
2 |
−ϕ ) |
(6.52) |
|
1 |
2 |
1 |
2 |
1 |
|
|
(теорема косинусов для треугольника, образованного векторами
A, A1 и A2 );
tgα = |
A1 sinϕ1 |
+ A2 sinϕ2 |
(6.53) |
||
A cosϕ |
|
||||
|
+ A cosϕ |
2 |
|
||
|
1 |
1 |
2 |
|
|
Если складываемые колебания будут иметь разные частоты, то изображающие их векторы A1 и A2 будут вращаться с разными угловыми скоростями, их относительное расположение будет периодически изменяться,
и длина вектора A уже не будет постоянной, а его вращение не будет равномерным. Таким образом, при сложении колебаний с разными частотами результирующее колебание уже не будет гармоническим.
Наиболее прост для рассмотрения и вместе с тем интересен случай, когда частоты складываемых колебаний мало отличаются друг от друга:
|
ω2 −ω1 |
|
= ∆ω <<ω1,ω2 . |
(6.54) |
|
|
Для удобства рассмотрения, положим амплитуды складываемых колебаний одинаковыми, а начальные фазы равными нулю. В этом случае
x(t) = x (t) + x |
|
(t) = Asin(ω t)+ Asin(ω |
t)= |
|
ω |
2 |
−ω |
|
|
|
ω |
+ω |
2 |
|
|||||
2 |
2Acos |
|
1 t |
sin |
1 |
|
t |
||||||||||||
1 |
|
1 |
2 |
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ω1 +ω2 |
|
(6.55) . |
||||
Так как ω1 |
и ω2 , величины одного порядка то обозначим |
|
|
=ω и, |
|||||||||||||||
|
|||||||||||||||||||
следовательно, |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||
|
|
|
∆ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
sin(ωt). |
|
|
|
|
|
|
(6.56) |
|||||||
|
|
|
x(t) = 2Acos |
2 |
t |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
107 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Стоит отметить, что колебание sin(ω t) происходит с частотой близкой к ω1 и ω2 .
|
∆ω |
t |
|
изменяется гораздо медленнее, чем |
В силу условия (6.54) cos |
2 |
|
sin(ωt), (рис. 6.9). Это дает возможность рассматривать результат сложе-
ния колебаний как гармоническое колебание с частотой ω, амплитуда которого медленно изменяется со временем. Такой колебательный процесс носит название биений. На рис. 6.9 сплошной линией показан график результирующего колебания, а штриховой — огибающая этого колебания
|
∆ω |
|
|
|
|
|
||
2Acos |
2 |
t |
. Как видно из рисунка амплитуда колебаний изменяется по |
|||||
закону |
A(t) = |
|
∆ω |
|
|
и соответственно период биений равен |
||
|
|
|||||||
|
2Acos |
t |
|
|||||
|
|
|
|
|
2 |
|
|
|
TБ = ∆2πω . Из условия (6.54) следует, что период биений TБ = ∆2πω >>T = 2ωπ
(рис. 6.9).
Рис. 6.9
108
Явление биений удобно использовать для сравнения частоты некоторого сигнала с частотой, принимаемой за эталон. Например, при сложении двух звуковых сигналов с близкими частотами будет слышна характерная пульсация громкости звука с периодом TБ . Это часто используется при на-
стройке музыкальных инструментов.
Если точка одновременно участвует в двух колебательных движениях во взаимно перпендикулярных направлениях:
x = Acos(ω1t), |
(6.57) |
|
|
y = B cos(ω2t +α), |
|
то говорят о сложении взаимно перпендикулярных колебаний. Для более наглядного описания можно представить ту же тележку с маятниковыми часами, только в данном случае тележка будет двигаться перпендикулярно плоскости качания маятника.
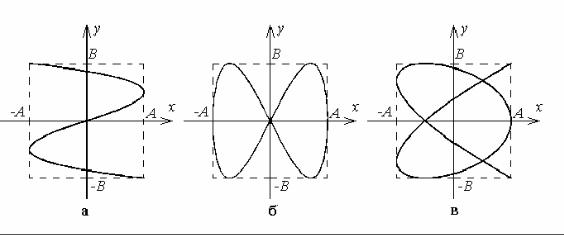
Если отношение частот в (6.57) выражается рациональным числом: ω1/ω2=m/n, где m, n — целые числа (в этом случае говорят, что частоты ω1 и ω2 соизмеримы), траектория движения точки будет представлять собой замкнутую кривую, так как через определенный промежуток времени (равный общему периоду колебаний, который определяется как наименьшее общее кратное периодов колебаний по х и по у) будут повторяться значения обеих координат. Эту кривую (их общее название — фигуры Лиссажу) мы можем наблюдать на экране электронного осциллографа, если на две пары его пластин подать сигналы с соизмеримыми частотами. По форме этой фигуры легко определить отношение частот колебаний по осям х и у: оно равно отношению числа касаний кривой Лиссажу с вертикальными и горизонтальными сторонами описанного прямоугольника соответственно. Так, на рис. 6.10 первая кривая Лиссажу соответствует ω1/ω2=3/1, вторая — ω1/ω2=1/2. Обратите внимание, что если кривая Лиссажу не замкнута (как на рис. 6.10,а), то при подсчете точек касания ее начало и конец учитываются с коэффициентом 1/2.
Рис. 6.10
109

Представляет интерес определение формы траектории из уравнений движения. Для решения этой задачи служат: основное тригонометрическое тождество, формулы синуса (косинуса) суммы, а также (при сложении колебаний с разными частотами) формулы тригонометрических функций кратного угла. Пусть складываемые колебания имеют одинаковую частоту, но различные начальные фазы.
|
|
x = Acosωt; |
|
(6.58) |
|
|
|
+α). |
|
или |
y = Bcos(ωt |
|
||
|
|
|
||
x |
= cosωt; |
|
|
|
|
|
|
|
|
A |
|
(6.59) |
||
y |
|
|
||
|
|
= cos(ωt +α) = cos(ωt) cosα − sin(ωt) sinα. |
|
|
|
|
|||
B |
|
|||
Для нахождения формы траектории необходимо исключить из этих уравнений время. Этого можно добиться, если возвести уравнения (6.59) в квадрат и применить основное тригонометрическое тождество, соответствующим образом группируя слагаемые в уравнениях. Получившееся уравнение
x2 |
− 2 |
xy |
cosα + |
y2 |
= sin2 |
α |
(6.60) |
|
A2 |
AB |
B2 |
||||||
|
|
|
|
|
задает эллипс, вписанный в прямоугольник размером 2А×2В и повернутый относительно осей координат на некоторый угол (рис. 6.11).
При некоторых значениях фазового сдвига α уравнение (6.60) принимает особенно простой вид:
а) при α = πk (k=0, ±1, ±2 и т. д.) эллипс вырождается в отрезок прямой;
б) при α = (2k+1)π/2 (k=0, ±1, ±2 и т. д.)
оси эллипса совпадают с осями координат.
Если же периоды колебаний по х и у не соизмеримы, траектория колеблющейся точки Рис. 6.11 будет постепенно заполнять весь прямо-
угольник 2А × 2В.
110
