659

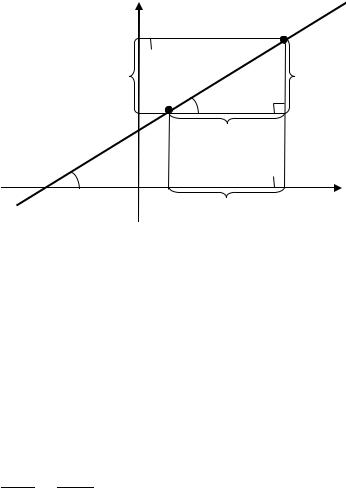
Глава 3. Прямая линия на плоскости

В этой главе будет рассмотрен такой простейший геометрический объект как прямая линия на плоскости. Прямая линия на плоскости – это линия, уравнение которой может быть записано в виде + + = 0, где , , – действительные числа, причём и одновременно не равны нулю, то есть 2 + 2 ≠ 0. Указанное уравнение является алгебраическим уравнением первой степени. Этому уравнению удовлетворяют координатыи любой точки, лежащей на прямой линии, и не удовлетворяют координаты и ни одной точки, не лежащей на прямой линии.

3.1. Угловой коэффициент прямой

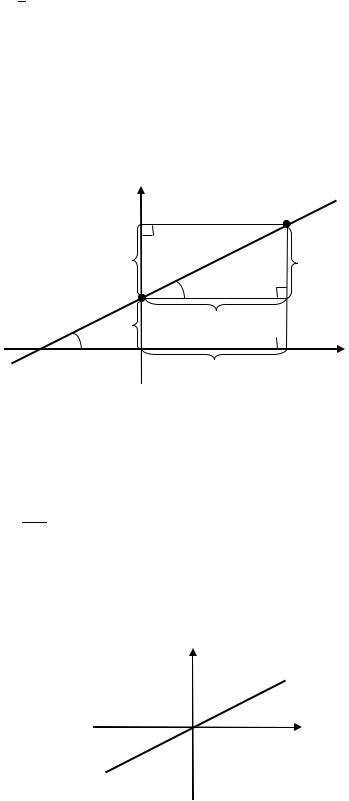
В прямоугольной системе координат рассмотрим прямую , не па-

Рис. 3.1. Нахождение углового коэффициента прямой

Угол называют углом наклона прямой. Тангенс угла наклона прямой называют угловым коэффициентом прямой, обозначают буквой и записывают:

= .

Угловой коэффициент прямой характеризует направление прямой. Достроим прямоугольный треугольник 1 2 . Для этого из точек

1 и 2 опустим перпендикуляры на оси и . Длина катета, параллельного оси , равна 2 − 1; длина катета, параллельного оси , равна

2 − 1.

В этом треугольнике выразим тангенс угла :

= | 2| = 2− 1 . | 1 | 2− 1

Учитывая, что = , получаем формулу для нахождения углового коэффициента прямой:

81

= 2− 1 .2− 1

Эта формула позволяет находить угловой коэффициент прямой по двум известным точкам этой прямой.

Если = 0, то = = 0 и прямая параллельна оси (рис. 3.2). В этом случае ординаты точек равны, то есть 1 = 2. Если = 2 , то

не существует и прямая параллельна оси , (рис. 3.3). В этом случае абсциссы точек равны, то есть 1 = 2.

Рис. 3.2. Прямая параллельна оси , = 0

Рис. 3.3. Прямая параллельна оси , не существует

Пример. 3.1. Найти угловой коэффициент прямой, проходящей через

точки: 1) 1(2; −4) и 2(5; 1); 2) 1(3; 2) и 2(7; 2); 3) 1(−1; −2) и2(−1; 4).

Решение. Для нахождения углового коэффициента прямой применя-

82

2 − 1 = 4 − (−2) = 6, 2 − 1 = −1 − (−1) = 0, и выражение для углового коэффициента не имеет смысла, то есть прямая параллельна оси

.

Ответ: 1) 53 ; 2) 0; 3) угловой коэффициент не определён.

3.2. Уравнение прямой с угловым коэффициентом

В прямоугольной системе координат рассмотрим прямую , не параллельную оси . Будем считать, что известен угловой коэффициент прямой и точка пересечения прямой с осью – точка (0; ), где – величина отрезка, отсекаемого прямой на оси . Пусть ( ; ) – произвольная точка прямой (рис. 3.4).

точки возьмём точку (0; ) и в качестве второй точки – точку ( ; ). С

учётом этого: 1 = 0, 1 = , 2 = , 2 = .

Тогда = −−0 . Отсюда: − = и = + .

Уравнение

= +

называется уравнением прямой с угловым коэффициентом.

Если = 0, то = и прямая проходит через начало координат

(рис. 3.5).

Рис. 3.5. Прямая, заданная уравнением =

83

Если = 0, то = . В этом случае прямая параллельна оси и отсекает на оси отрезок, величина которого равна (рис. 3.6).

Рис. 3.6. Прямая, заданная уравнением =

Если не существует, то прямая параллельна оси и задаётся уравнением = , где – величина отрезка, отсекаемого прямой на оси

(рис. 3.7).

Решение. Уравнение прямой с угловым коэффициентом имеет вид= + . Среди приведённых уравнений такому виду соответствуют уравнения под номерами 3), 5), 9), 11).

Ответ: 3), 5), 9), 11).

Пример. 3.3. Прямая задана уравнением = −4 + 3. Найти угловой коэффициент прямой и величину отрезка, отсекаемого прямой на оси ординат.

Решение. Прямая задана уравнением с угловым коэффициентом =+ , где – угловой коэффициент прямой, – величина отрезка, отсекаемого прямой на оси . С учётом этого получаем: = −4, = 3.

Ответ: = −4, = 3.

84

Пример. 3.4. Составить уравнение прямой, зная, что её угловой ко-

эффициент равен 2 и величина отрезка, отсекаемого прямой на оси ординат,

3

равна −1.

Решение. Учитывая уравнение прямой с угловым коэффициентом= + , где – угловой коэффициент прямой, – величина отрезка, от-

секаемого прямой на оси ординат, получаем: = 23 − 1.

Ответ: = 23 − 1.

Пример. 3.5. Составить уравнение прямой, проходящей через начало координат и наклонённой к оси абсцисс под углом 1350.

Решение. Воспользуемся уравнением прямой с угловым коэффициентом и проходящей через начало координат: = , где – угловой коэффициент прямой. Найдём угловой коэффициент прямой. Учитывая, что= и по условию = 1350, а также применяя формулы приведения,

получаем: = 1350 = (900 + 450) = − 450 = −1. Тогда уравне-

ние искомой прямой: = − .

Ответ: = − .

Пример. 3.6. Найти угол наклона прямой к оси :

Решение. Найдём угол наклона прямой, учитывая, что тангенс угла наклона прямой к оси – это угловой коэффициент прямой: = . Учтём, также, что все прямые, кроме 5), заданы уравнением с угловым коэффициентом: = + . На основании этого запишем тангенс угла наклона прямой и затем найдём угол наклона прямой:

1)= 1 и = 4 ;

2)= √33 и = 6 ;

3)= −√3 и = 23 ;

4)= 0 и = 0.

Решение. Если точка лежит на прямой, то её координаты должны удовлетворять уравнению этой прямой. Если точка не лежит на прямой, то её координаты не удовлетворяют уравнению этой прямой. Будем подставлять координаты каждой точки в данное уравнение.

Подставляем координаты точки (2; 2): 2 = 2 ∙ 2 − 5. Отсюда 2 ≠ −1 и точка не лежит на прямой и, следовательно, прямая не проходит через точку .

85

Подставляем координаты точки (0; −5): −5 = 2 ∙ 0 − 5. Отсюда −5 = −5 и точка лежит на прямой и, следовательно, прямая проходит через точку .

Подставляем координаты точки (12 ; −4): −4 = 2 ∙ 12 − 5. Отсюда

−4 = −4 и точка лежит на прямой и, следовательно, прямая проходит через точку .

Подставляем координаты точки (12 ; 4): 4 = 2 ∙ 12 − 5. Отсюда 4 ≠

−4 и точка не лежит на прямой и, следовательно, прямая не проходит через точку .

Подставляем координаты точки (−1; 0): 0 = 2 ∙ (−1) − 5. Отсюда 0 ≠ −7 и точка не лежит на прямой и, следовательно, прямая не проходит через точку .

Подставляем координаты точки (13 ; − 133 ): − 133 = 2 ∙ 13 − 5. Отсюда

− 133 = − 133 и точка лежит на прямой и, следовательно, прямая проходит

через точку .

Так как прямая, проходящая через начало координат, задаётся уравнением = , то данная прямая = 2 − 5 через точку (0; 0) не проходит.

Ответ: прямая проходит через точки , , и не проходит через точки , , , .

Пример. 3.8. Точки , , , , лежат на прямой = −3 − 1. Абсциссы этих точек соответственно равны −2; 0; 4; − 13 ; 15 . Найти ординаты

этих точек.

Решение. Для нахождения ординат точек подставим их абсциссы в данное уравнение.

Если = −2, то = −3 ∙ (−2) − 1 = 5. Если = 0, то = −3 ∙ 0 − 1 = −1. Если = 4, то = −3 ∙ 4 − 1 = −13.

Решение. Для построения прямой достаточно знать две её точки. Все прямые, кроме 10) и 11), заданы уравнением с угловым коэффициентом =+ , где – угловой коэффициент прямой, – величина отрезка, отсека-

86

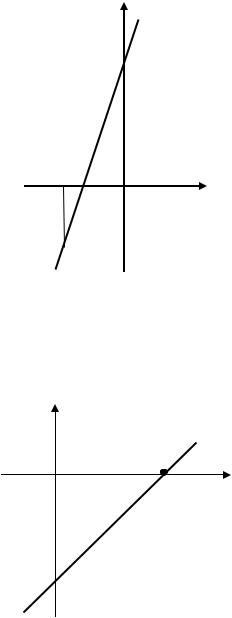
емого прямой на оси . Поэтому для данных прямых известна точка их пересечения с осью ординат: (0; ). Осталось найти ещё одну точку.

1)Прямая, заданная уравнением = 3 + 4, пересекает ось ординат

вточке (0; 4). Найдём вторую точку. Возьмём, например, = −2, тогда= −2 и вторая точка прямой (−2; −2) (рис. 3.8).

4

−2

−2

Рис. 3.8. Прямая, заданная уравнением = 3 + 4 (к Примеру 3.9)

2) Прямая, заданная уравнением = − 2, пересекает ось ординат в точке (0; −2). Найдём вторую точку. Возьмём, например, = 2, тогда= 0 и вторая точка прямой (2; 0) (рис. 3.9).

−2

Рис. 3.9. Прямая, заданная уравнением = − 2 (к Примеру 3.9)

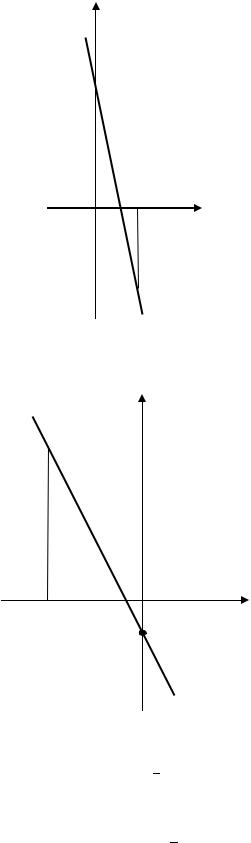
3)Прямая, заданная уравнением = −5 + 3, пересекает ось ординат в точке (0; 3). Найдём вторую точку. Возьмём, например, = 1, тогда

= −2 и вторая точка прямой (1; −2) (рис. 3.10).

4)Прямая, заданная уравнением = −2 − 1, пересекает ось ординат в точке (0; −1). Найдём вторую точку. Возьмём, например, = −3, тогда = 5 и вторая точка прямой (−3; 5) (рис. 3.11).

87

3

1

−2

Рис. 3.10. Прямая, заданная уравнением = −5 + 3 (к Примеру 3.9)

5

Рис. 3.11. Прямая, заданная уравнением = −2 − 1 (к Примеру 3.9)

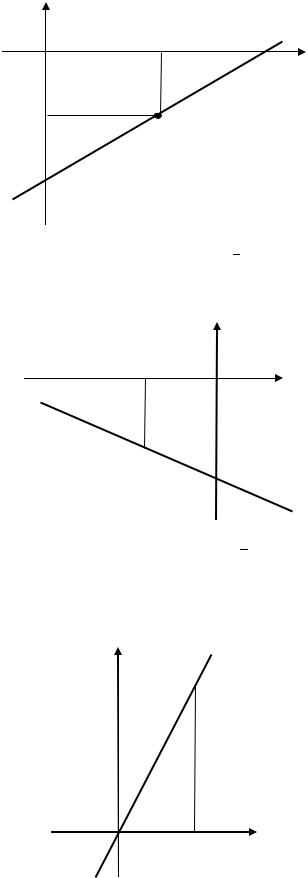
5) Прямая, заданная уравнением = 13 − 4, пересекает ось ординат в точке (0; −4). Найдём вторую точку. Возьмём, например, = 6, тогда

= −2 и вторая точка прямой (6; −2) (рис. 3.12).

6)Прямая, заданная уравнением = − 12 − 3, пересекает ось орди-

= −2,точке (0; −3). Найдём вторую точку. Возьмём, например,нат в

тогда = −2 и вторая точка прямой (−2; −2) (рис. 3.13).

88

6

−2

−4

Рис. 3.12. Прямая, заданная уравнением = 13 − 4 (к Примеру 3.9)

−2

−2

−3

Рис. 3.13. Прямая, заданная уравнением = − 12 − 3 (к Примеру 3.9)

7) Прямая = 2 задана уравнением вида = . Такая прямая всегда проходит через начало координат. Найдём вторую точку. Возьмём, например, = 2, тогда = 4 и вторая точка прямой (2; 4) (рис. 3.14).

4

2

Рис. 3.14. Прямая, заданная уравнением = 2 (к Примеру 3.9)

89

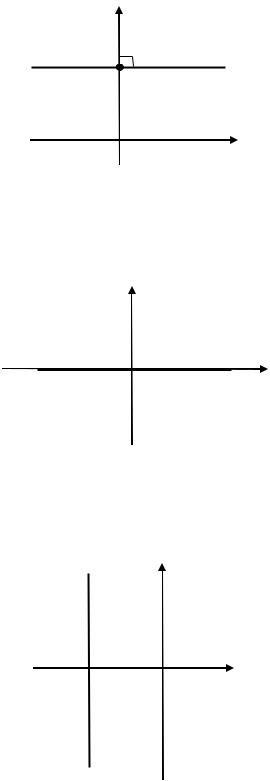
8) Прямая, заданная уравнением = 5, пересекает ось ординат в точке (0; 5) и параллельна оси (рис. 3.15).

5

Рис. 3.15. Прямая, заданная уравнением = 5 (к Примеру 3.9)

9) Прямая, заданная уравнением = 0, представляет множество точек, ординаты которых равны нулю, то есть прямая совпадает с осью

(рис. 3.16).

Рис. 3.16. Прямая, заданная уравнением = 0 (к Примеру 3.9)

10) Прямая, заданная уравнением = −3, представляет множество точек, абсциссы которых равны −3, то есть прямая параллельна оси

(рис. 3.17).

Рис. 3.17. Прямая, заданная уравнением = −3 (к Примеру 3.9)

90