
659
.pdf
11) Прямая, заданная уравнением = 0, представляет множество точек, абсциссы которых равны нулю, то есть прямая совпадает с осью
(рис. 3.18).
Рис. 3.18. Прямая, заданная уравнением = 0 (к Примеру 3.9)
3.3. Уравнение прямой с данным угловым коэффициентом и проходящей через данную точку
В прямоугольной системе координат рассмотрим прямую, не параллельную оси . Будем считать, что известен угловой коэффициент прямойи одна точка прямой 0( 0; 0). Пусть ( ; ) – произвольная точка прямой.
Для составления уравнения прямой воспользуемся формулой углово-
го коэффициента прямой по двум известным точкам прямой: = 2− 1 . За-
2− 1
пишем формулу углового коэффициента для точек 0( 0; 0) и ( ; ):
= − 0 . Выразим отсюда − 0:
− 0
− 0 = ( − 0).
Полученное уравнение называется уравнением прямой с данным уг-
ловым коэффициентом и проходящей через данную точку.
Если угловой коэффициент не задан, то полученное уравнение определяет множество прямых, проходящих через точку 0. Множество таких прямых называют пучком прямых, проходящих через точку 0. Более подробно о пучке прямых будет сказано в п. 3.12.
Пример. 3.10. Составить уравнение прямой, проходящей через точку(−1; 4) и имеющей угловой коэффициент, равный 3.
Решение. Воспользуемся уравнением прямой с данным угловым коэффициентом и проходящей через данную точку: − 0 = ( − 0). По условию задачи: 0 = −1, 0 = 4, = 3. Получаем: − 4 = 3( − (−1)).
После преобразований получаем: = 3 + 7.
Ответ: = 3 + 7.
91
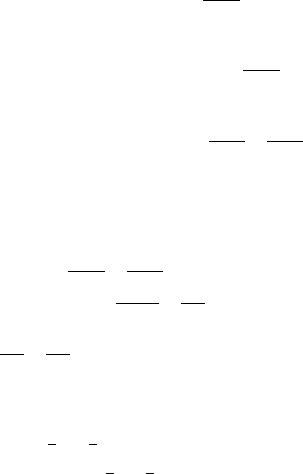
Пример. 3.11. Составить уравнение прямой, проходящей через точку(5; −2) и составляющей с осью абсцисс угол = 450.
Решение. Найдём угловой коэффициент прямой, используя формулу
= :
= 450 = 1.
Далее воспользуемся уравнением прямой, когда известен угловой коэффициент прямой и точка прямой: − 0 = ( − 0).
Получаем:
− (−2) = 1 ∙ ( − 5).
Преобразуем к уравнению с угловым коэффициентом = + :
= − 7.
Ответ: = − 7.
3.4. Уравнение прямой, проходящей через две данные точки
В прямоугольной системе координат рассмотрим прямую, не параллельную оси . Будем считать, что известны две точки прямой: 1( 1; 1) и 2( 2; 2). Пусть ( ; ) – произвольная точка прямой.
Воспользуемся формулой углового коэффициента прямой по двум
известным точкам прямой: = 2− 1 . Далее воспользуемся уравнением
2− 1
прямой с данным угловым коэффициентом и проходящей через данную точку. В качестве данной точки возьмём точку 1( 1; 1):
− 1 = 2− 1 ( − 1).
2− 1
Преобразуем уравнение: разделим уравнение на 2 − 1 и поменяем
левую и правую части уравнения местами:
− 1 = − 1 .
2− 1 2− 1
Полученное уравнение называется уравнением прямой, проходящей через две данные точки.
Пример. 3.12. Составить уравнение прямой, проходящей через две
точки 1(−2; 3) и 2(4; 1).
Решение. Воспользуемся уравнением прямой, проходящей через две
данные точки: − 1 = − 1 . В условиях задачи: 1 = −2, 1 = 3, 2 = 4,
2− 1 2− 12 = 1. Подставляем: 4−(−2)−(−2) = 1−3−3 .
Преобразуем к уравнению с угловым коэффициентом:
+2 = −3
6 −2
−2( + 2) = 6( − 3) −2 − 4 = 6 − 18 6 = −2 + 14
= − 13 + 73 .
Ответ: = − 13 + 73 .
Пример. 3.13. Даны вершины треугольника (4; −3), (−2; −5),(1; 1). Составить уравнение медианы, проведённой из вершины .
92
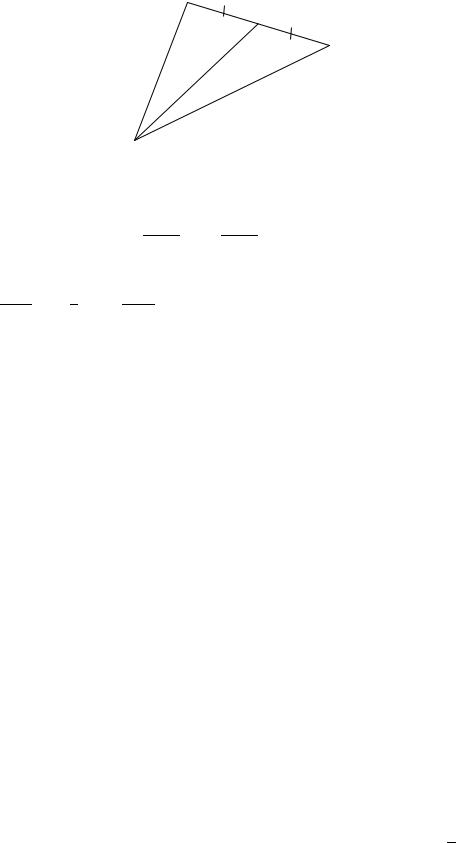
Решение. Обозначим середину стороны через . Тогда – искомая медиана (рис. 3.19).
Рис. 3.19. Треугольник и медиана (к Примеру 3.13)
Найдём координаты точки , используя формулы нахождения координат середины отрезка: = 1+2 2, = 1+2 2 . В условиях задачи: 1 = −2,
1 = −5, 2 = 1, 2 = 1.
Получаем:
= −2+12 = − 12 , = −5+12 = −2.
|
Координаты точки : (− |
1 |
; −2). |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||
|
Далее для составления уравнения медианы воспользуемся урав- |
||||||||||||||||||||||||||||||
нением прямой, проходящей через две точки: |
− 1 |
= |
− 1 |
. В условиях за- |
|||||||||||||||||||||||||||
− |
1 |
− |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
2 |
1 |
|
|||
дачи: |
= 4, |
= −3, |
= − |
, = −2. |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||
1 |
|
|
|
|
1 |
2 |
2 |
2 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
−4 |
|
|
−(−3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
= |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
−1−4 |
−2−(−3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Преобразуем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
−4 |
= |
+3 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
− |
2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1( − 4) = − |
( + 3) |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
2( − 4) = −9( + 3) |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
2 − 8 = −9 − 27 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
9 = −2 − 19 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
= − |
2 |
− |
19 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
9 |
|
|
|
2 |
|
19 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Ответ: = − |
− |
. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
3.5. Общее уравнение прямой
Рассмотрим уравнение первой степени: + + = 0, где , ,
– действительные числа, причём и одновременно не равны нулю, то есть 2 + 2 ≠ 0. Выразим из уравнения . Для этого слагаемое оставим в левой части, остальные слагаемые перенесём в правую часть: =
= − − . Далее, разделив уравнение на ( ≠ 0), получаем: = − −
93
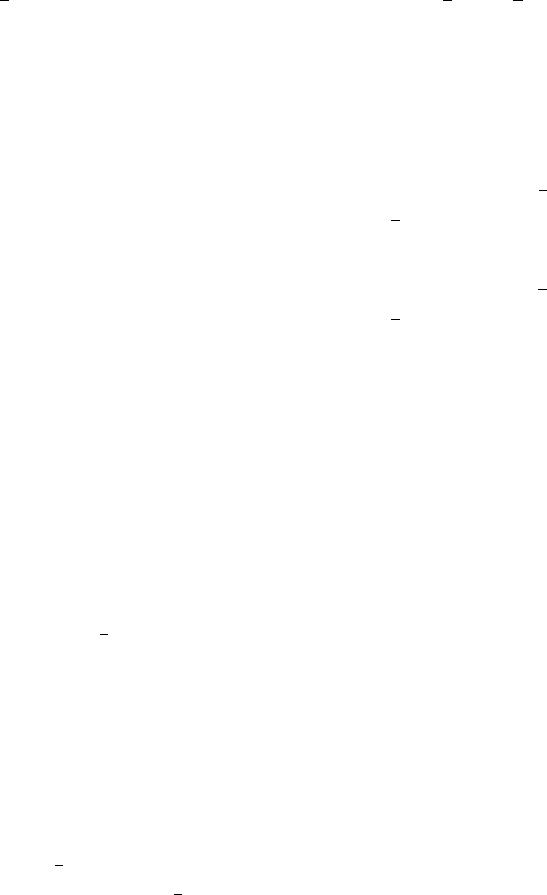
− . Полученное уравнение имеет вид = + , где = − , = − , то
есть представляет собой уравнение прямой с угловым коэффициентом. Таким образом, уравнение
+ + = 0,
где 2 + 2 ≠ 0, определяет прямую и называется общим уравнением пря-
мой.
Если = 0, то уравнение имеет вид + = 0. Это уравнение определяет прямую, проходящую через начало координат, так как точка(0; 0) удовлетворяет этому уравнению: ∙ 0 + ∙ 0 = 0 0 = 0.
Если = 0, то уравнение имеет вид + = 0. Выразим : = − , то есть получили уравнение вида = , где = − . Уравнение =
определяет прямую, параллельную оси . Если = 0, то прямая совпадает с осью .
Если = 0, то уравнение имеет вид + = 0. Выразим : = − , то есть получили уравнение вида = , где = − . Уравнение =
определяет прямую, параллельную оси . Если = 0, то прямая совпадает с осью .
Пример. 3.14. Среди приведённых уравнений указать общие уравне-
ния прямой: |
|
|
|
|
|
|
|
|
|
|
|
|
|||
1) 2 + 3 + 4 = 0; |
2) = 5 − 4; |
3) − 4 = 0; |
|||||||||||||
4) |
3 |
+ |
4 |
− 2 = 0; |
5) = 0; |
6) 3 2 − 2 2 − 1 = 0; |
|||||||||
|
|
||||||||||||||
5 |
|
5 |
|
|
|
|
|
|
|
|
|
||||
7) 4 − 5 2 = 0; |
8) |
+ |
= 1; |
9) 4 − 5 = 0; |
|||||||||||
|
|
||||||||||||||
|
|
|
|
|
|
3 |
|
2 |
|
1 |
|
|
|||
10) 2 |
+ 2 = 4; |
11) = |
− 1; |
12) 8 − 7 = 0. |
|||||||||||
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
||||
Решение. Общее уравнение |
прямой имеет вид + + = 0. |
||||||||||||||
Среди приведённых уравнений такому виду соответствуют уравнения под номерами 1), 3), 4), 5), 9), 12).
Ответ: 1), 3), 4), 5), 9), 12).
Пример. 3.15. Преобразовать уравнение прямой с угловым коэффициентом = − 43 + 2 к общему уравнению.
Решение. Преобразуем данное уравнение к общему уравнению прямой + + = 0. Умножим данное уравнение на 3. Получаем: 3 = = −4 + 6. Затем перенесём все слагаемые в левую часть: 4 + 3 − 6 = 0.
Ответ: 4 + 3 − 6 = 0.
Пример. 3.16. Преобразовать общее уравнение прямой 6 + 3 − −7 = 0 к уравнению прямой с угловым коэффициентом.
Решение. Преобразуем данное уравнение к уравнению прямой с угловым коэффициентом = + . Выразим из уравнения . Для этого слагаемое 3 оставим в левой части, остальные слагаемые перенесём в правую
часть: 3 = −6 + 7. Далее, разделив уравнение на 3 , получаем: = = −2 + 73 .
Ответ: = −2 + 73
94

Пример. 3.17. Дана прямая 2 − 3 − 3 = 0. Проверить, проходит ли
она через точки (3; 1), (−1; − 53), (−1; 53), (1; −2), (32 ; 0), (13 ; 12),(0; 0).
Решение. Если точка лежит на прямой, то её координаты должны удовлетворять уравнению этой прямой. Если точка не лежит на прямой, то её координаты не удовлетворяют уравнению этой прямой. Будем подставлять координаты каждой точки в данное уравнение.
Подставляем координаты точки (3; 1): 2 ∙ 3 − 3 ∙ 1 − 3 = 0. Отсюда 0 = 0 и точка лежит на прямой и, следовательно, прямая проходит через точку .
Подставляем координаты точки (−1; − 53): 2 ∙ (−1) − 3 ∙ (− 53) −
−3 = 0. Отсюда 0 = 0 и точка лежит на прямой и, следовательно, прямая проходит через точку .
Подставляем координаты точки (−1; 53): 2 ∙ (−1) − 3 ∙ 53 − 3 = 0.
Отсюда −10 ≠ 0 и точка не лежит на прямой и, следовательно, прямая не проходит через точку С.
Подставляем координаты точки (1; −2): 2 ∙ 1 − 3 ∙ (−2) − 3 = 0. Отсюда 5 ≠ 0 и точка не лежит на прямой и, следовательно, прямая не проходит через точку .
Подставляем координаты точки (32 ; 0): 2 ∙ 32 − 3 ∙ 0 − 3 = 0. Отсюда
0 = 0 и точка лежит на прямой и, следовательно, прямая проходит через точку .
Подставляем координаты точки (13 ; 12): 2 ∙ 13 − 3 ∙ 12 − 3 = 0. Отсюда
− 236 ≠ 0 и точка не лежит на прямой и, следовательно, прямая не прохо-
дит через точку .
Подставляем координаты точки (0; 0): 2 ∙ 0 − 3 ∙ 0 − 3 = 0. Отсюда −3 ≠ 0 и точка не лежит на прямой и, следовательно, прямая не проходит через точку .
Ответ: прямая проходит через точки , , и не проходит через точки , , , .
Пример. 3.18. Точки , , , , лежат на прямой 3 − 2 − 6 = 0. Абсциссы этих точек соответственно равны −2; 0; 3; 12 ; − 13 . Найти ордина-
ты этих точек.
Решение. Приведём данное общее уравнение прямой к уравнению прямой с угловым коэффициентом = + . Получаем: = 32 − 3. Для нахождения ординат точек подставим их абсциссы в полученное уравнение.
Если = −2, то = 32 ∙ (−2) − 3 = −6. Если = 0, то = 32 ∙ 0 − 3 = −3. Если = 3, то = 32 ∙ 3 − 3 = 32 .
Если = 12 , то = 32 ∙ 12 − 3 = − 49.
95
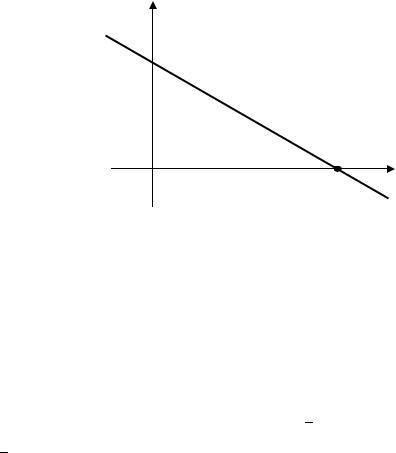
Если = − |
1 |
|
, то = |
3 |
|
∙ (− |
1 |
) − 3 = − |
7 |
. |
|
|
|
|
|||
|
|
|
|
|
|
|
|
||||||||||
3 |
|
2 |
3 |
3 |
2 |
9 |
|
7 |
|
||||||||
Ответ: , = −6; , = −3; , = |
; , = − |
; , = − |
. |
||||||||||||||
|
|
|
|||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
4 |
2 |
||||||
Пример. 3.19. Построить прямые, заданные следующими уравнени- |
|||||||||||||||||
ями: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1) + 2 − 4 = 0; |
2) 5 − 3 + 2 = 0; |
|
3) 3 + 4 = 0; |
||||||||||||||
4) 2 − = 0; |
5) 3 − 5 = 0; |
|
6) 2 + 1 = 0; |
||||||||||||||
7) − 1 = 0; |
|
|
|
8) 3 + 2 = 0; |
|
9) = 0; |
|||||||||||
10) = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решение. Все прямые заданы общим уравнением + + = 0. Для построения прямой достаточно знать две её точки. Для этого зададим, например, переменной числовое значение и вычислим соответствующее значение переменной . Или, можно, наоборот, задать переменной числовое значение и вычислить соответствующее значение переменной .
1) Рассмотрим прямую, заданную уравнением + 2 − 4 = 0. Зададим = 0, тогда = 2. Получаем точку прямой (0; 2). Затем зададим = 0, тогда = 4. Получаем вторую точку прямой (4; 0). Через точки и проводим прямую (рис. 3.20).
2 
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
||
|
|
Рис. 3.20. Прямая, заданная уравнением + 2 − 4 = 0 |
|||||||||
|
|
|
|
|
|
|
(к примеру 3.19) |
|
|
|
|
|
2) Рассмотрим прямую, заданную уравнением 5 − 3 + 2 = 0. Зада- |
||||||||||
дим = 0, |
тогда = |
2 |
. Получаем точку прямой (0; |
2 |
). Затем зададим |
||||||
|
|
||||||||||
|
|
3 |
|
|
3 |
|
|
||||
= 0, |
тогда = − |
2 |
. |
Получаем вторую точку прямой |
|
(− |
2 |
; 0). Через |
|||
|
|
|
|||||||||
|
|
5 |
|
|
|
|
5 |
||||
точки и проводим прямую (рис. 3.21).
3) Рассмотрим прямую, заданную уравнением 3 + 4 = 0. В уравнении отсутствует числовое слагаемое , поэтому прямая проходит через
начало координат. Зададим = 2, тогда = − 32 . Получаем точку прямой
(2; − 32). Через точки и проводим прямую (рис. 3.22).
4)Рассмотрим прямую, заданную уравнением 2 − = 0. В уравнении отсутствует числовое слагаемое , поэтому прямая проходит через начало координат. Зададим = 2, тогда = 4. Получаем точку прямой
(2; 4). Через точки и проводим прямую (рис. 3.23).
96

 2 3
2 3
− |
2 |
|
|
5 |
|
|
Рис. 3.21. Прямая, заданная уравнением 5 − 3 + 2 = 0 (к примеру 3.19)
2
|
|
− 32 
Рис. 3.22. Прямая, заданная уравнением 3 + 4 = 0 (к примеру 3.19)
5) Рассмотрим прямую, заданную уравнением 3 − 5 = 0. В уравнении отсутствует числовое слагаемое , поэтому прямая параллельна оси
. Выразим из уравнения : = 53 . Прямая пересекает ось в точке
(53 ; 0) (рис. 3.24).
6)Рассмотрим прямую, заданную уравнением 2 + 1 = 0. В уравне-
нии отсутствует числовое слагаемое , поэтому прямая параллельна оси
. Выразим из уравнения : = − |
1 |
. Прямая пересекает ось в точке |
||
|
||||
|
1 |
2 |
|
|
(− |
; 0) (рис. 3.25). |
|
||
|
|
|||
2 |
|
|
|
|
97
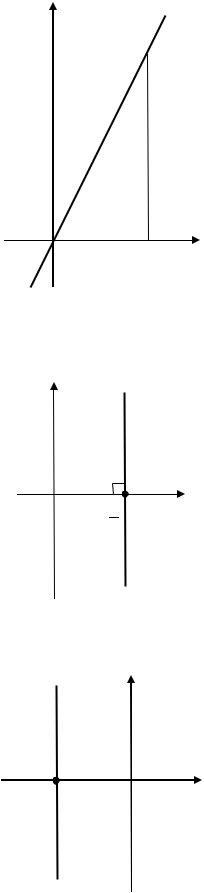
4 
|
2 |
|
|
|
Рис. 3.23. Прямая, заданная уравнением 2 − = 0 (к примеру 3.19)
|
|
|
|
5 |
|
|
3 |
|
Рис. 3.24. Прямая, заданная уравнением 3 − 5 = 0 (к примеру 3.19)
|
|
|
|
|
|
|
|
|
|
||
− |
1 |
|
|
|
|
2 |
|
|
|
|
|
Рис. 3.25. Прямая, заданная уравнением 2 + 1 = 0 (к примеру 3.19)
98
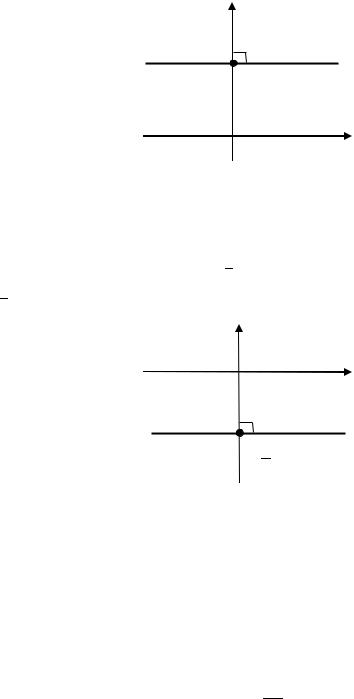
7) Рассмотрим прямую, заданную уравнением − 1 = 0. В уравнении отсутствует числовое слагаемое , поэтому прямая параллельна оси. Выразим из уравнения : = 1 . Прямая пересекает ось в точке
(0; 1) (рис. 3.26).
1
Рис. 3.26. Прямая, заданная уравнением − 1 = 0 (к примеру 3.19)
8) Рассмотрим прямую, заданную уравнением 3 + 2 = 0. В уравнении отсутствует числовое слагаемое , поэтому прямая параллельна оси
. Выразим из уравнения : = − 23 . Прямая пересекает ось в точке
(0; − 23) (рис. 3.27).
|
|
|
|
|
|
|
− |
2 |
|
3 |
Рис. 3.27. Прямая, заданная уравнением 3 + 2 = 0 (к примеру 3.19)
9) Рассмотрим прямую, заданную уравнением = 0. Прямая представляет множество точек, абсциссы которых равны нулю, то есть прямая совпадает с осью (рис. 3.28).
10) Рассмотрим прямую, заданную уравнением = 0. Прямая представляет множество точек, ординаты которых равны нулю, то есть прямая совпадает с осью (рис. 3.29).
Пример. 3.20. Составить уравнение прямой, проходящей через начало координат, зная, что длина её отрезка, заключённого между прямыми
2 − + 10 = 0 и 2 − + 5 = 0, равна √10.
Решение. Искомая прямая проходит через начало координат, поэтому её уравнение можно записать в виде = . Данные прямые обозначим через 1 и 2 соответственно. Точки пересечения искомой прямой с данными прямыми обозначим через ( 1; 1) и ( 2; 2) соответственно (рис. 3.30).
99
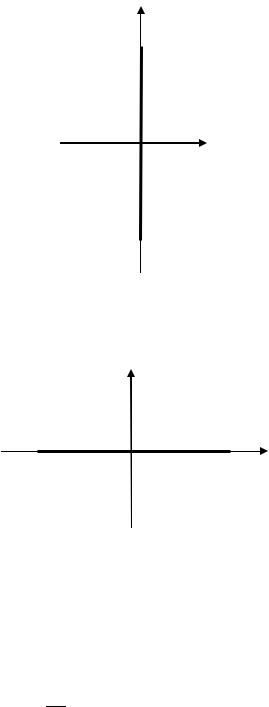
Рис. 3.28. Прямая, заданная уравнением = 0 (к примеру 3.19)
|
|
Рис. 3.29. Прямая, заданная уравнением = 0 (к примеру 3.19)
Так как точка лежит на прямой 1, то её координаты удовлетворяют уравнению этой прямой. Можно записать: 2 1 − 1 + 10 = 0. Так как точкалежит на прямой 2, то её координаты удовлетворяют уравнению этой прямой. Можно записать: 2 2 − 2 + 5 = 0.
Применяя формулу расстояния между двумя точками, запишем квад-
рат расстояния между точками и :
| |2 = ( 2 − 1)2 + ( 2 − 1)2.
Учитывая, что = √10, запишем уравнение:
( 2 − 1)2 + ( 2 − 1)2 = 10.
Так как точки и лежат на прямой = , то их координаты удовлетворяют уравнениям этих прямых. Можно записать:
1 = 1, 2 = 2.
Полученные уравнения объединим в систему:
100
