
659
.pdf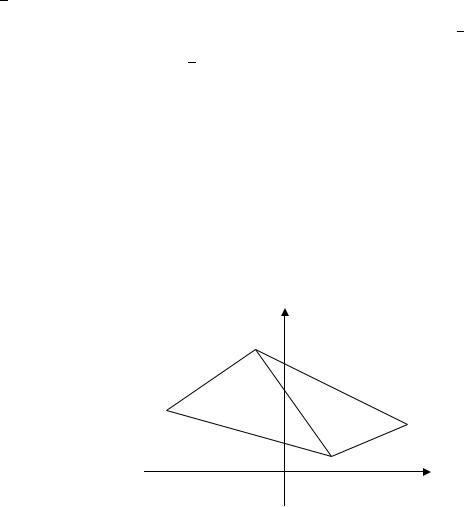
Решение первого уравнения: = 5. Решение второго уравнения: =
− 13 .
Получаем два варианта для искомой точки: (5; 0), (− 13 ; 0).
Ответ: (5; 0), (− 13 ; 0).
Пример 2.20. Даны последовательные вершины однородной четырёхугольной пластины (2; 1), (5; 3), (−1; 7), (−7; 5). Определить координаты её центра масс.
Указание. Если однородную пластину разбить на две части и найти центр масс каждой из них, то центр масс исходной пластины находится в точке, которая делит расстояние между центрами масс каждой из частей в отношении, обратном отношению их площадей. Центр масс треугольника находится в точке пересечения его медиан.
Решение. Разобьём четырёхугольник на два треугольника и(рис. 2.21). Найдём центр масс каждого из них, используя результат Примера 2.15.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
Рис. 2.21. Центр масс четырёхугольника (к Примеру 2.20) |
||||||||||||||||||||||||||||||||||||
Центр масс треугольника : |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
= |
1+ 2+ 3 |
= |
2+5−1 |
|
= 2 , = |
1+ 2+ 3 |
= |
1+3+7 |
= |
11 |
. |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
3 |
|
|
|
|
3 |
|
|
11 |
|
|
|
3 |
|
|
|
3 |
|
|
3 |
|
|
|
|
|
|
|
|||||||||
Получили точку ′ (2; |
) – центр масс треугольника . |
||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Центр масс треугольника : |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
= |
1+ 2+ 3 |
= |
2−1−7 |
|
= −2 , = |
1+ 2+ 3 |
= |
1+7+5 |
= |
|
13 |
. |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|||||||||||||||||||||||||
|
|
3 |
|
|
|
|
3 |
|
|
|
|
13 |
|
3 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|||||||||||
Получили точку ′′ (−2; |
) |
– центр масс треугольника . |
|||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Далее найдём площади треугольников и . |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
± |
|
= |
1 |
|
| 2 − 1 |
2 − 1| = |
1 |
|
| 5 − 2 3 − 1| = |
1 |
| 3 2| = 12, |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
∆ |
2 |
|
3 − 1 |
3 − 1 |
|
|
|
2 −1 − 2 7 − 1 |
|
|
|
|
|
2 −3 6 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
то есть ∆ = 12. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
± ∆ = |
1 |
| 2 − 1 |
2 − 1 |
| = |
1 |
|−1 − 2 |
7 − 1| |
= |
1 |
|−3 6| = 21, |
|||||||||||||||||||||||||||
|
3 − 1 |
|
|
||||||||||||||||||||||||||||||||||
|
|
2 |
|
3 − 1 |
|
|
|
|
2 −7 − 2 5 − 1 |
|
|
|
|
|
|
2 −9 4 |
|||||||||||||||||||||
то есть ∆ = 21.
41
Находим центр масс исходной пластины, учитывая, что он находится в точке, которая, согласно указанию к задаче, делит расстояние между точ-
ками ′ и ′′ в отношении = |
|
|
|
21 |
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
= |
|
|
= |
|
: |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
12 |
4 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
7 |
|
|
|
|
|
|
|
|
|
11 |
7 13 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
= |
1+ 2 |
= |
2+4∙(−2) |
= − |
6 |
, = |
1+ 2 |
= |
3 |
+4∙ |
3 |
= |
135 |
= |
45 |
. |
||||||||
1+ |
7 |
|
|
|
7 |
|
|
|
||||||||||||||||
|
|
1+ |
4 |
|
11 |
|
|
|
|
1+ |
|
1+ |
4 |
|
33 |
11 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Таким образом, получили точку (− 116 ; 4511) – центр масс исходной
пластины.
Ответ: (− 116 ; 4511).
Пример 2.21. Прямая определена двумя своими точками (−1; 4) и(2; 1). На этой же прямой найти точку, абсцисса которой равна 5.
Решение. Обозначим искомую точку (5; ). Точки , , лежат на одной прямой. Используя условие расположения трёх точек на одной пря-
мой:
2− 1 = 2− 1 ,
3− 1 3− 1
получаем:
2−(−1)5−(−1) = 1−4−4 , 36 = −3−4 ,
= −2.
Тогда искомая точка: (5; −2).
Ответ: (5; −2).
2.6. Полярная система координат
Полярная система координат определяется полюсом и полярной осью. Полюс – это неподвижная точка, полярная ось – это луч, выходящий из полюса и вращающийся вокруг него. Полюс обозначим буквой , полярную ось – буквой (рис. 2.22).
|
|
Рис. 2.22. Полярная система координат
В полярной системе координат точка определяется двумя координатами: – угол поворота полярной оси и – расстояние от полюса до точки. Обозначение: ( ; ). Число называется полярным радиусом, число называется полярным углом. Для построения точки в полярной системе координат полярную ось поворачивают на угол и на полученном луче находят точку, расстояние которой от полюса равно (рис. 2.23).
Пример 2.22. Построить в полярной системе координат точку
(2; 34 ).
42
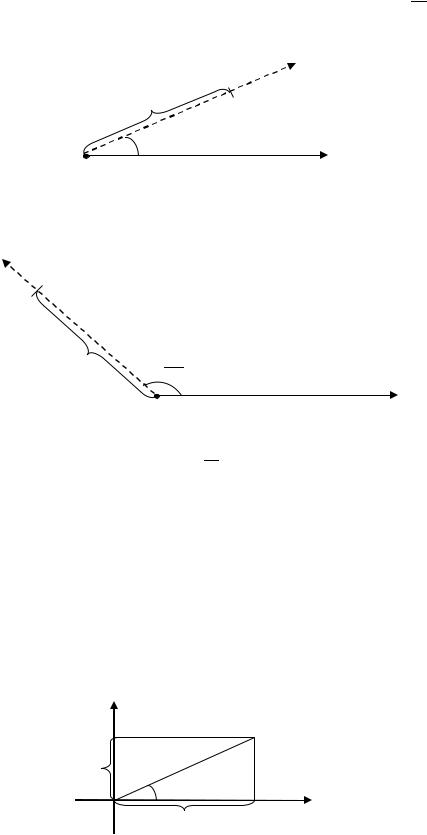
Решение. Повернём полярную ось вокруг полюса на угол = 34 и на
полученном луче отложим от полюса отрезок длины 2. Получим точку
(рис. 2.24).
|
|
Рис. 2.23. Построение точки в полярной системе координат
23
4
|
|
Рис. 2.24. Построение точки (2; 34 ) в полярной системе координат (к Примеру 2.22)
Установим связь между полярной системой координат и прямоугольной декартовой системой координат. Для этого совместим обе системы координат: полюс полярной системы совместим с началом координат декартовой системы, полярный луч совместим с положительной частью оси
Ox.
Пусть точка в прямоугольной декартовой системой координат имеет координаты (; ), в полярной системе координат имеет координаты (; ) . Из точки опустим перпендикуляры на оси Ox и Oy. Основания перпендикуляров обозначим и соответственно (рис. 2.25).
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
Рис. 2.25. Совмещение полярной и прямоугольной декартовой систем координат
Из прямоугольного треугольника :
43
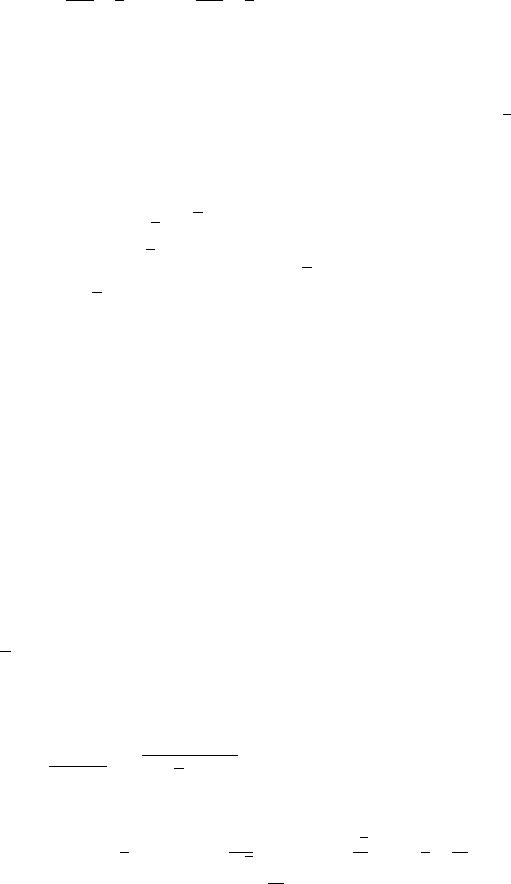
cos = | | = , sin = | | = .
Отсюда:
= cos , = sin .
Эти формулы позволяют найти прямоугольные координаты точки через её полярные координаты.
Пример 2.23. В полярной системе координат дана точка (2; 6).
Найти прямоугольные координаты этой точки при условии, что ось абсцисс совпадает с полярной осью, начало координат совпадает с полюсом.
Решение. По формулам, выражающим прямоугольные координаты
через полярные, получаем:
= cos = 2 cos 6 = √3 ,= sin = 2 sin 6 = 1.
Прямоугольные координаты точки: (√3; 1).
Ответ: (√3; 1).
Получим формулы, выражающие полярные координаты точки через её прямоугольные координаты.
Из прямоугольного треугольника (рис. 2.25) найдём полярный |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
радиус и полярный угол : |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
= √( )2 + ( )2 = √( )2 + ( )2 = √ 2 + 2; |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
| | |
|
| | |
|
|
|
|
|
|
|
|
|
|
|
|||||
= |
|
|
|
|
= |
|
|
= |
|
|
. |
|
|
|
|
|
|
|
|
|
| |
| |
|
| | |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
С учётом расположения точки в определённой координатной четвер- |
||||||||||||||||||||
ти можно записать следующую формулу нахождения полярного угла : |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
, |
|
или четвертям, |
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
= |
+ |
|
, |
четверти, |
|||||||||||||
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
{ − + |
|
|
, |
четверти. |
||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
Здесь (− ; ]. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Пример |
2.24. |
В прямоугольной |
системе координат дана точка |
|||||||||||||||||
(−√3; 1). Найти полярные координаты этой точки при условии, что ось абсцисс совпадает с полярной осью, начало координат совпадает с полюсом.
Решение.
Найдём полярный радиус точки:
= √ 2 + 2 = √(−√3)2 + 12 = 2.
Найдём полярный угол точки, учитывая, что она расположена во второй четверти:
= + = + −1√3 = − √33 = − 6 = 56 .
Полярные координаты точки: (2; 56 ).
44
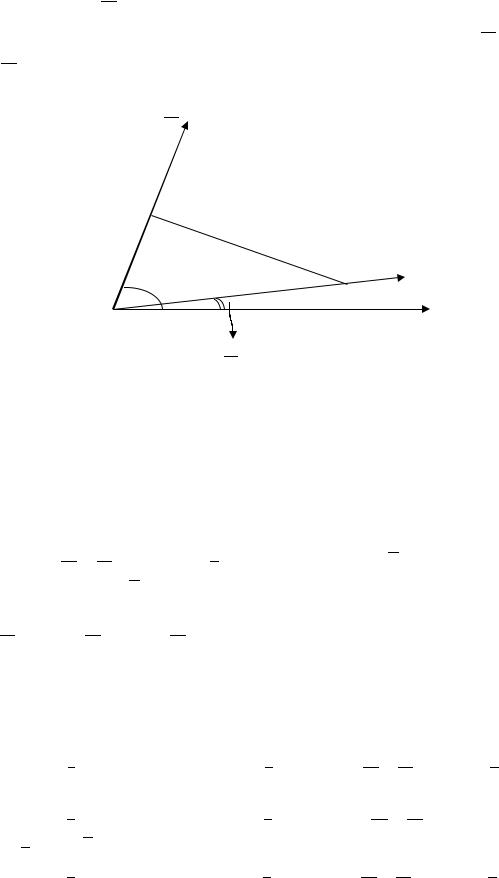
Ответ: (2; 56 ).
Пример 2.25. Вычислить расстояние между точками (2; 12) и
(1; 512), заданными в полярной системе координат. Решение. Сделаем чертёж (рис. 2.26).
5
12
1 |
|
|
|
|
|
|
5 |
|
|
||
|
2 |
|
|
||
|
|
12 |
|||
12 |
|
||||
|
|
|
|
||
|
|
|
|
||
12
Рис. 2.26. Расстояние между точками в полярной системе координат (к Примеру 2.25)
Для нахождения расстояния между точками и применим теорему косинусов для треугольника (квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения
этих сторон на косинус угла между ними):
| |2 = | |2 + | |2 − 2 ∙ | | ∙ | | cos = 22 + 12 − −2 ∙ 2 ∙ 1 cos (512 − 12) = 5 − 4 cos 3 = 3. Отсюда | | = √3.
Ответ: | | = √3.
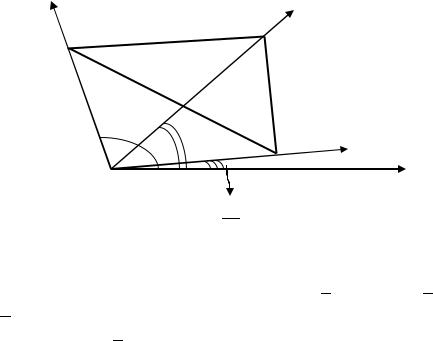
Пример 2.26. Вычислить площадь треугольника, вершины которого(9; 10), (12; 415), (10; 35 ) заданы в полярной системе координат.
Решение. Сделаем чертёж (рис. 2.27). Площадь треугольника найдём как комбинацию площадей треугольников , , :
∆ = ∆ + ∆ − ∆ .
Площади треугольников будем находить как половину произведения смежных сторон треугольника на синус угла между ними:
∆ = 12 ∙ | | ∙ | | = 12 ∙ 9 ∙ 12 (415 − 10) = 54 sin 6 =
= 27,
∆ = 12 ∙ | | ∙ | | = 12 ∙ 12 ∙ 10 (35 − 415) = = 60 sin 3 = 30√3,
∆ = 12 ∙ | | ∙ | | = 12 ∙ 9 ∙ 10 (35 − 10) = 45 sin 2 =
= 45.
45
3 |
|
|
|
|
|
|
|
4 |
||||
|
|
|
|
|
|
|
|
|
||||
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
12 |
|
|
|
|
|
|
|
||
|
3 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
4 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
5 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||||
|
|
15 9 |
|
|
|
|||||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
10 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10
Рис. 2.27. Площадь треугольника в полярной системе координат (к Примеру 2.26)
Тогда ∆ = ∆ + ∆ − ∆ = 27 + 30√3 − 45 = 30√3 − −18 = 6(5√3 − 3).
Ответ: ∆ = 6(5√3 − 3).
2.7. Преобразование координат на плоскости
Рассмотрим две прямоугольные системы координат и установим связь между координатами точки в этих системах. Рассмотрим три случая.
1.Меняется положение начала координат, а направление осей и масштаб не меняются. Такое преобразование называется параллельным сдвигом осей.
2.Обе оси поворачиваются в одну сторону на один и тот же угол, а начало координат и масштаб не меняются. Такое преобразование называется поворотом осей.
3.Меняется положение начала координат и обе оси поворачиваются
водну сторону на один и тот же угол, масштаб не меняется. Такое преобразование называется параллельным сдвигом осей с последующим их поворотом.
Преобразование координат при параллельном сдвиге осей
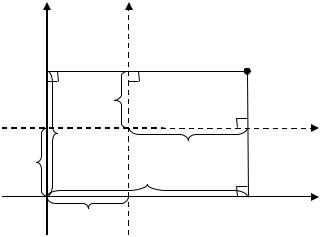
Рассмотрим систему координат . Эту систему называют старой системой координат. В этой системе отметим точку ′(; ). Через точку ′ проведём новые оси ′ ′ и ′ ′ параллельно старым осям. Получим новую систему ′ ′ ′. Пусть точка относительно старой системы имеет координаты: (; ), относительно новой системы: ( ′; ′) (рис. 2.28).
Опустим из точки перпендикуляры на оси координат. Основания перпендикуляров на осях и обозначим соответственно и , на осях ′ ′ и ′ ′ обозначим соответственно ′ и ′. Точку пересечения
оси ′ ′ с осью обозначим ′ , точку пересечения оси ′ ′ с осью
обозначим ′ .
46
′
|
|
′ |
|
|
|
|
|||
|
|
|
|
|
|
′ |
|
|
|
′ |
|
|
|
′ |
|
|
|
|
|
|
′ |
′ |
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.28. Преобразование координат при параллельном сдвиге осей
По чертежу можно записать следующие равенства:
| |
| = | ′ |
| + | ′ | = | ′ | + | ′ |
′|, |
||||
|
|
|
|
|
|
|
|
| |
| = | ′ |
| + | ′ |
|
| = | ′ |
| + | ′ |
|
′|. |
|
|
|
|
|
|
|
|
Переходя к координатам, получаем следующие формулы:
{ = + ′,= + ′.
или
{ = ′ + ,= ′ + .
Эти формулы называют формулами преобразования координат при параллельном сдвиге осей. Они позволяют найти координаты точки в старой
системе, зная координаты точки в новой системе. Выразим отсюда ′ и ′:
{ ′ = − ,′ = − .
Эти формулы также называют формулами преобразования координат при параллельном сдвиге осей. Они позволяют найти координаты точки в новой системе, зная координаты точки в старой системе.
Пример 2.27. Формулы преобразования координат заданы следующими равенствами: = ′ − 2, = ′ + 1. Определить старые координаты начала ′ новой системы.
Решение. Данные формулы представляют формулы преобразования координат при параллельном сдвиге осей: = ′ + , = ′ + , где и
– старые координаты начала ′ новой системы. Сравнивая формулы, полу-
чаем: ′(−2; 1). Ответ: ′(−2;1).
Пример 2.28. Написать формулы преобразования координат, если начало координат перенесено в точку ′(−3;2). Направление осей и масштаб сохранены.
Решение. Воспользуемся формулами преобразования координат при
параллельном сдвиге осей: = ′ + , = ′ + . Учитывая, что = −3,
= 2, получаем: = ′ − 3, = ′ + 2. Ответ: = ′ − 3, = ′ + 2.
47

Пример 2.29. Дана точка (3; −2). Найти координаты этой точки в новой системе, если начало координат перенесено в точку ′(−1;4), направление осей и масштаб сохранены.
Решение. Применяя формулы преобразования координат при парал-
лельном сдвиге осей, получаем:
′ = − = 3 − (−1) = 4, ′ = − = −2 − 4 = −6.
Координаты точки в новой системе: (4; −6).
Ответ: (4; −6).
Преобразование координат при повороте осей
Рассмотрим систему координат . Эту систему называют старой системой координат. Повернём оси и на угол . Получим новые оси′ и ′. Угол – угол поворота, то есть угол между осями и ′, и ′. Получим новую систему ′ ′. Пусть точка относительно старой
системы имеет координаты: ( ; ), относительно новой системы:
( ′; ′) (рис. 2.29).
′ |
|
|
|
||
|
||
|
|
′
|
|
|
|
′ |
|
|
|
|
|
′ |
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.29. Преобразование координат при повороте осей |
|
|||||||||||||
Опустим из точки перпендикуляры на оси координат. Основания |
|||||||||||||||
перпендикуляров на осях и обозначим соответственно |
и , на |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
осях ′ и ′ |
обозначим соответственно ′ |
и ′. Проведём отрезок |
|||||||||||||
̅̅̅̅̅ |
|
|
|
|
|
|
|
|
|
|
|
̅̅̅̅̅ |
|
|
|
, длину отрезка обозначим . Угол между отрезком и осью обо- |
|||||||||||||||
|
|
|
|
|
|
̅̅̅̅̅ |
и осью |
′ |
обозначим 2. Тогда 1 = |
||||||
значим 1, угол между отрезком |
|
||||||||||||||
2 + . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из прямоугольного треугольника (рис. 2.29): |
|
|
|
||||||||||||
|
| | |
|
| | |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||||
cos = |
|
|
, sin = |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
| | |
1 |
| | |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||||
Отсюда:
| | = | | cos 1, | | = | | sin 1.
Учитывая, что | | = , | | = , | | = , получаем:
= cos 1 = cos( 2 + ) = (cos 2 cos − sin 2 sin ) =
48
=( cos 2) cos − ( sin 2) sin ;
= sin 1 = sin( 2 + ) = (sin 2 cos + cos 2 sin ) =
=( sin 2) cos + ( cos 2) sin .
Из прямоугольного треугольника ′ (рис. 2.29):
cos 2 = |
| ′| |
|
, sin 2 |
= |
| ′ | |
. |
| | |
|
|||||
|
|
|
| | |
|||
Отсюда: |
|
|
|
|
|
|
| ′| = | | cos 2, | ′ | = | | sin 2.
Учитывая, что | | = , ′ = ′, ′ = ′, получаем:
′ = cos 2, ′ = sin 2.
Выражения для и принимают вид:
= ′ cos − ′ sin , = ′ cos + ′ sin = ′ sin + ′ cos .
Таким образом получены следующие формулы:
= ′ cos − ′ sin , { = ′ sin + ′ cos .
Эти формулы называют формулами преобразования координат при повороте осей. Они позволяют найти координаты точки в старой системе, зная координаты точки в новой системе.
Получим формулы, позволяющие найти координаты точки в новой системе, зная координаты точки в старой системе. Для этого решим полученную систему линейных алгебраических уравнений по правилу Крамера относительно неизвестных ′ и ′. Перепишем систему в виде:
′ cos − ′ sin = , |
|
|||||||||||||
{ ′ sin + ′ cos = . |
|
|||||||||||||
Вычислим определитель системы ∆: |
||||||||||||||
∆= |cos |
|
|
|
− sin | = 1. |
||||||||||
|
sin |
|
|
|
cos |
|
|
|
|
|||||
Далее вычислим определители ∆ ′ и ∆ ′: |
||||||||||||||
∆ ′= | |
|
|
− sin |
| |
= cos + sin , |
|||||||||
|
|
|
|
cos |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
cos |
|
|
|
|
|
|
|||||
∆ ′= |sin |
| = cos − sin = − sin + cos . |
|||||||||||||
Тогда неизвестные ′ и ′: |
||||||||||||||
′ = |
|
∆ |
|
′ |
|
|
cos + sin |
|
|
|
||||
|
|
|
= |
|
|
|
|
|
|
= cos + sin , |
||||
|
∆ |
|
|
|
|
1 |
|
|
||||||
′ = |
|
∆ ′ |
= |
− sin + cos |
|
= − sin + cos . |
||||||||
|
∆ |
|
|
|||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|||
Таким образом: |
|
′ |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
= cos + sin , |
|||
|
|
|
|
|
|
|
|
|
|
|
{ ′ = − sin + cos . |
|||
К этим формулам можно прийти другим способом. Старую систему можно получить из новой поворотом её на угол − . Поэтому в формулах, выражающих старые координаты точки через новые, заменим на − , на
′, ′ на , на ′, ′ на . Получим следующие формулы:
′ = cos + sin , { ′ = − sin + cos .
49

Эти формулы также называют формулами преобразования коорди-
нат при повороте осей. Они позволяют найти координаты точки в новой системе, зная координаты точки в старой системе.
Пример 2.30. Определить угол , на который повёрнуты оси, если формулы преобразования координат заданы следующими равенствами: =
12 ′ − √23 ′, = √23 ′ + 12 ′.
Решение. Сравним данные формулы с формулами преобразования координат при повороте осей: = ′ cos − ′ sin , = ′ sin +
+ ′ cos . Отсюда: cos = 12 , sin = √23 и угол поворота: = 3 .
Ответ: = 3 .
Пример 2.31. Написать формулы преобразования координат, если координатные оси повёрнуты на угол = − 6 . Начало координат и мас-
штаб сохранены.
Решение. Воспользуемся формулами преобразования координат при повороте осей: = ′ cos − ′ sin , = ′ sin + ′ cos . Учитывая, что
= − 6 , получаем:
= ′ cos (− 6) − ′ sin (− 6) = √23 ′ + 12 ′,
= ′ sin + ′ cos = ′ sin (− 6) + ′ cos (− 6) = − 12 ′ + √23 ′.
Ответ: = √23 ′ + 12 ′, = − 12 ′ + √23 ′.
Пример 2.32. Дана точка (1; −1). Найти координаты этой точки в новой системе, если оси координат повёрнуты на угол в 450, начало координат и масштаб сохранены.
Решение. Применяя формулы преобразования координат при пово-
роте осей, получаем:
′ = cos + sin = 1 ∙ cos 450 + (−1) ∙ sin 450 = 0,
′ = − sin + cos = − 1 sin 450 + (−1) ∙ 450 = − √2.
Координаты точки в новой системе: (0; −√2).
Ответ: (0; −√2).
Преобразование координат при параллельном сдвиге осей с последующим их поворотом
Рассмотрим систему координат . Эту систему называют старой системой координат. В этой системе отметим точку ′( ; ). Через точку ′ проведём новые оси ′ ′′ и ′ ′′ параллельно старым осям. Получим вспо-
могательную систему ′ ′′ ′′. Повернём систему ′ ′′ ′′ на угол . Угол
– угол поворота, то есть угол между осями ′ ′′ и ′ ′, ′ ′′ и ′ ′. Получим новую систему ′ ′ ′. Пусть точка относительно старой системы имеет координаты: ( ; ), относительно новой системы: ( ′; ′), относительно вспомогательной системы ( ′′; ′′)
(рис. 2.30).
50
