Решение системы оду методом Рунге-Кутта с автоматическим выбором шага интегрирования (Rkadapt)
Функция Rkadapt возвращает матрицу S1 размерности (n+1)*m значений решения системы n - уравнений в m - точках интервала интегрирования методом Рунге-Кутта с автоматическим выбором шага изменения аргумента. Уравнения заданы вектором правых частей (производных) уравнений D(t,Y) и начальными условиями, определёнными вектором Y0.
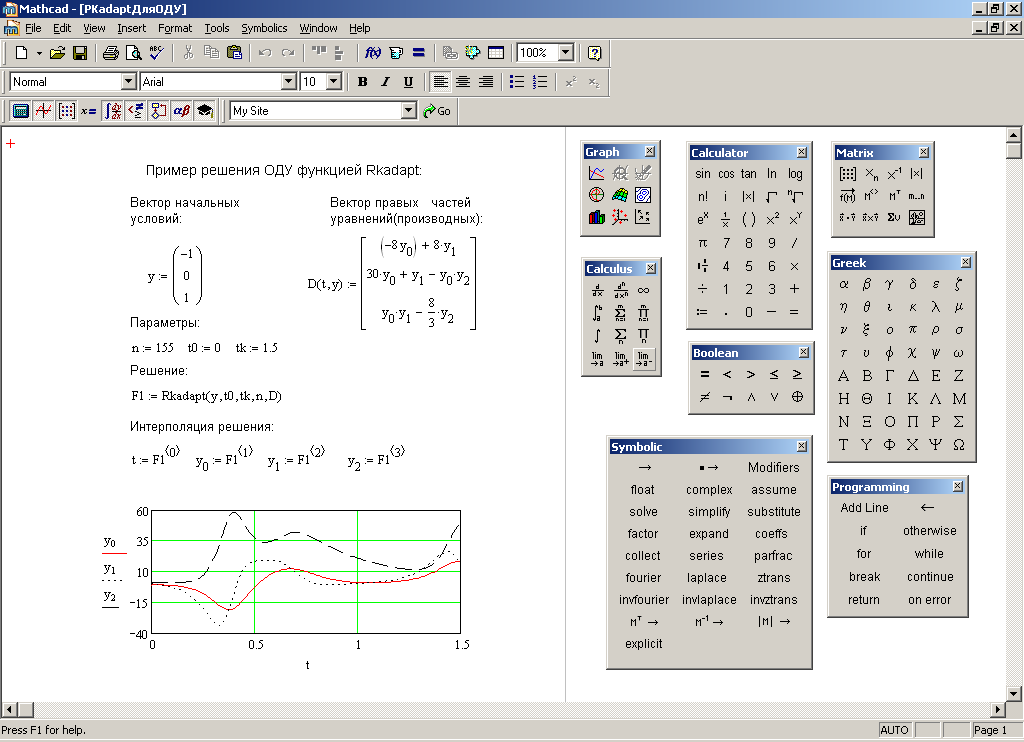
Рис. 5. Решение системы ОДУ методом Рунге-Кутта
с автоматическим выбором шага интегрирования (функция Rkadapt).
Обращение к функции имеет вид: Rkadapt(Y0, t1, t2, m, D), где m- число точек, в которых отыскивается решение.
Результат решения выводится в виде матрицы, поэтому для дальнейшего использования, например для построения графиков решения, его необходимо преобразовать в систему функций. На рис. 5 приведен пример решения системы ОДУ функцией Rkadapt c выводом решения в виде системы графиков. Для этого матрица решения так же должна быть интерполирована системой функций (см. формулы 3).
3. Решение системы оду методом Булирша – Штера (функция Bulstoer)
В общем случае интегрирования системы уравнений с переменным шагом обращение к функции имеет вид: bulstoer(Y, t0, t1, m, D, kmax, s),
где Y - вектор начальных условий;
t0, t1 - начальная и конечная точки интервала интегрирования;
m - число шагов интегрирования;
Y - вектор правых частей(производных) уравнений;
kmax - максимальное число промежуточных точек интегрирования;
s - минимальный интервал (шаг) между промежуточными точками.
Рис. 6. Пример решения системы ОДУ с использованием функции Bulstoer
с фиксированным шагом интегрирования
Если используется метод решения с постоянным шагом, то обращение к функции упрощается и имеет вид: bulstoer(Y, t0, t1, m, D).
Как и в случае применения методов Рунге-Кутта решение системы уравнений выводится в матричной форме, поэтому оно должно быть интерполировано для последующего использования в вычислительном процессе.
Пример применения метода Bulirsch –Stoer’а для решения системы ОДУ приведен на рис.6. Для сравнения методов в качестве примера рассмотрена та же система уравнений, что и на рис. 5.
5. Решение системы оду методом Розенброка (функция Radau)
Если система дифференциальных уравнений записана в матричной форме, а коэффициенты при неизвестных функциях значительно, например, на несколько порядков величины, отличаются друг от друга, то такую матрицу называют вырожденной, а систему уравнений «жёсткой».
Решение «жёсткой» системы уравнений методом Рунге – Кутта приводит к необходимости уменьшения (измельчения) шага интегрирования, что в свою очередь приводит к накоплению ошибок интегрирования, и как следствие, к неустойчивости решения. Поэтому для решения таких систем разработан специальный алгоритм, названный по имени его автора, методом Розенброка. Метод позволяет получить решение как «жёстких» обыкновенных дифференциальных уравнений одной переменной, так и систем уравнений. В MathCad этот алгоритм реализуется функцией Radau.
В общем случае обращение к функции имеет вид: Radau (y, x1, x2, num, D, kmax, s), в котором аргументы: y, x1, x2, num, D, kmax, s, имеют тот же смысл, что и в рассмотренных выше решающих функциях. В частном случае фиксированного шага интегрирования обращение к функции упрощается - Radau (y, x1, x2, num, D).
На рис.7 приведен пример решения системы ОДУ, элементы матрицы которой отличаются примерно на четыре порядка.
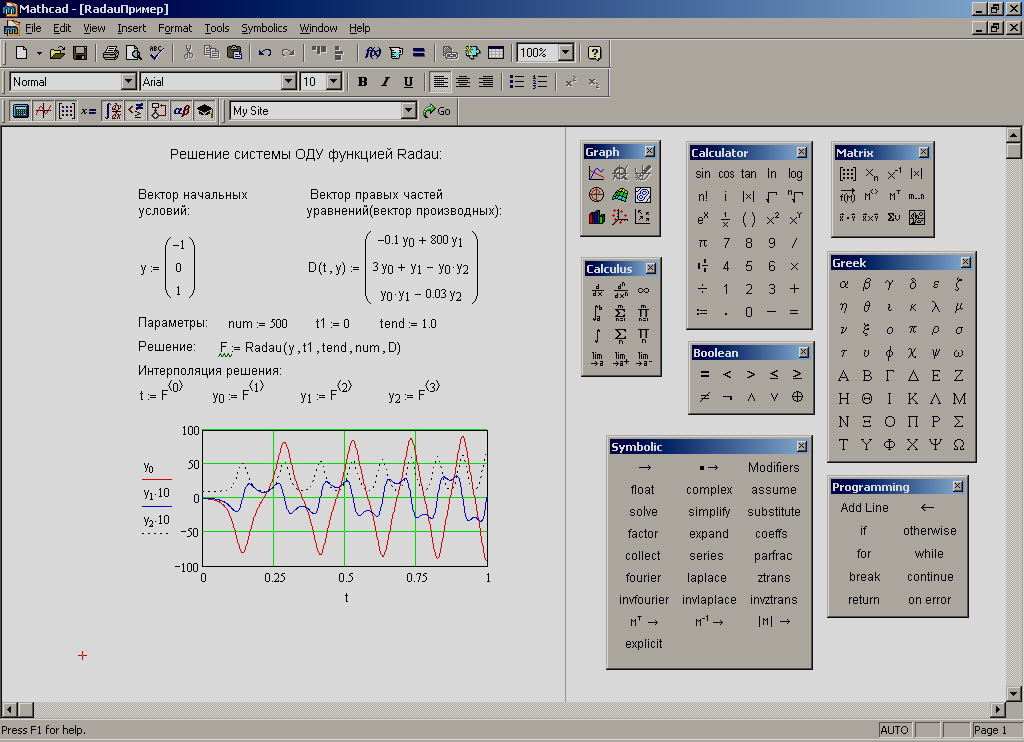
Рис. 7. Пример решения системы ОДУ функцией Radau