2. Решение систем оду первого порядка

Для решения в MathCad системы уравнений любым из рассмотренных ниже методов исходная, т.е. записанная в математической форме система уравнений:

, , (1)

где t- аргумент(обычно подразумевается время),

f_k(t,y₁,y₂,…y_n) - заданная функция своих аргументов, должна быть преобразована к виду:

, (2)

где Y - вектор (матрица-столбец) искомых функций,

D(t,Y) - вектор (матрица-столбец) значений производных – вектор правых частей системы уравнений в любой точке решения, представленного в виде матрицы-столбца (Y(t).

Использование решающего блока Given …Odesolve является одним из способов решения систем ОДУ первого порядка. На рабочем листе система уравнений должна быть записана с производными слева, порядок записи начальных условий несущественен. Как и ранее правая часть уравнений отделяется от левой символом эквивалентности (выделенный знак равенства). Пример решения системы 3-х уравнений приведен на рис.3.

2. Решение системы оду методом Рунге-Кутта

Кроме блока Given…Odesolve в MathCad имеется ещё несколько функций, реализующих классические алгоритмы численного решения задачи Коши для систем обыкновенных дифференциальных уравнений. Важнейшими из них являются методы Рунге-Кутта интегрирования уравнений с фиксированным (rkfixed) шагом и с переменным шагом (Rkadapt), которые практически всегда приводят к решению. Аналогичные задачи позволяет решать и метод Булирша-Штера( Bulirsch-Stoer) с переменным и фиксированным шагом (функция Bulstoer), который в некоторых случаях даёт более точное решение при меньших затратах машинного времени. Для решения систем с вырожденной матрицей ОДУ предназначена функция Radau, которая реализует метод Розенброка.

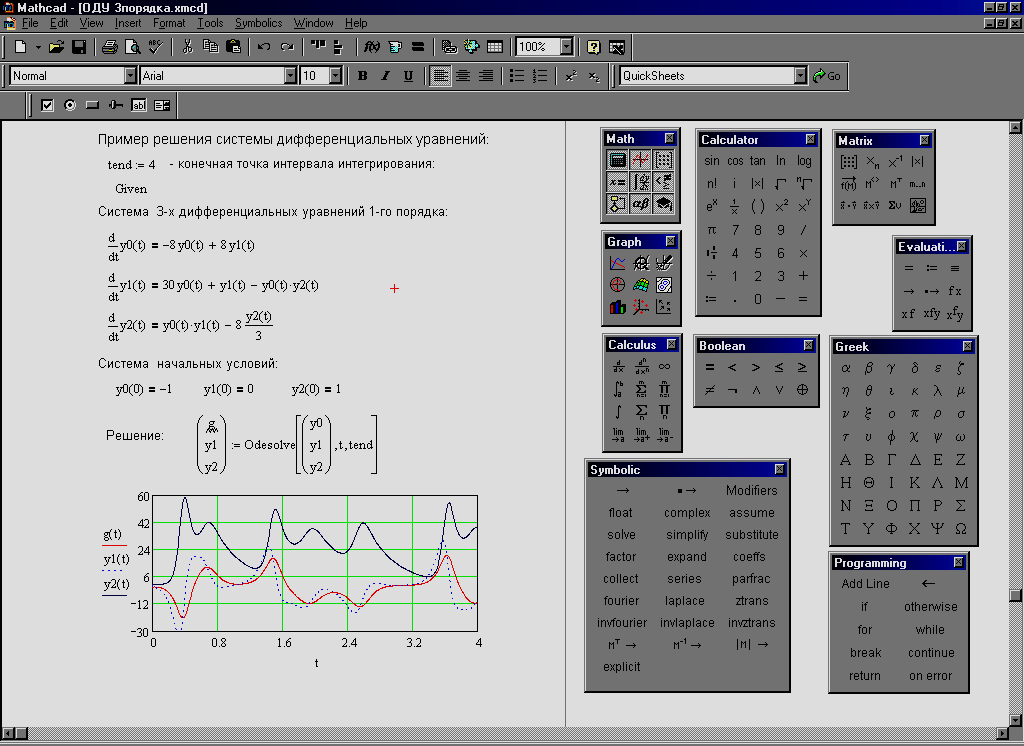
Рис. 3. Пример решения системы ОДУ решающим блоком

Given …Odesolve.

2.1. Решение системы оду методом Рунге-Кутта с фиксированным шагом интегрирования (функция rkfixed)

Функция rkfixed возвращает матрицу S1 размерности (n+1)*npoits значений решения системы n - обыкновенных дифференциальных уравнений на отрезке [t0, t1] изменения аргумента t, определенного производными в векторе D(t,Y) и начальными условиями, заданными вектором Y0, методом Рунге-Кутта с постоянным (заданным) шагом изменения аргумента. Параметр n -точек задаёт число строк в матрице результата. Очевидно, чем больше число n-точек , тем точнее аппроксимация решения. Пример решения ОДУ методом Рунге-Кутта представлен на рис.4.

Обращение к функции имеет вид: rkfixed(Y, t0, t1, npoints, D).

Для решения системы уравнений с использованием этой функции необходимо:

• присвоить начальное t0 и конечное значения t1 отрезка интегрирования (аргумента t);

• задать (присвоить) число точек интегрирования (параметр npoints);

• cоздать вектор начальных условий с именем Y0 размерности n;

• создать вектор D(t,Y) правых частей системы уравнений – производных, размерностью n;

• напечатать решение: S1:= rkfixed(Y0, t0,t1, npoints, D).

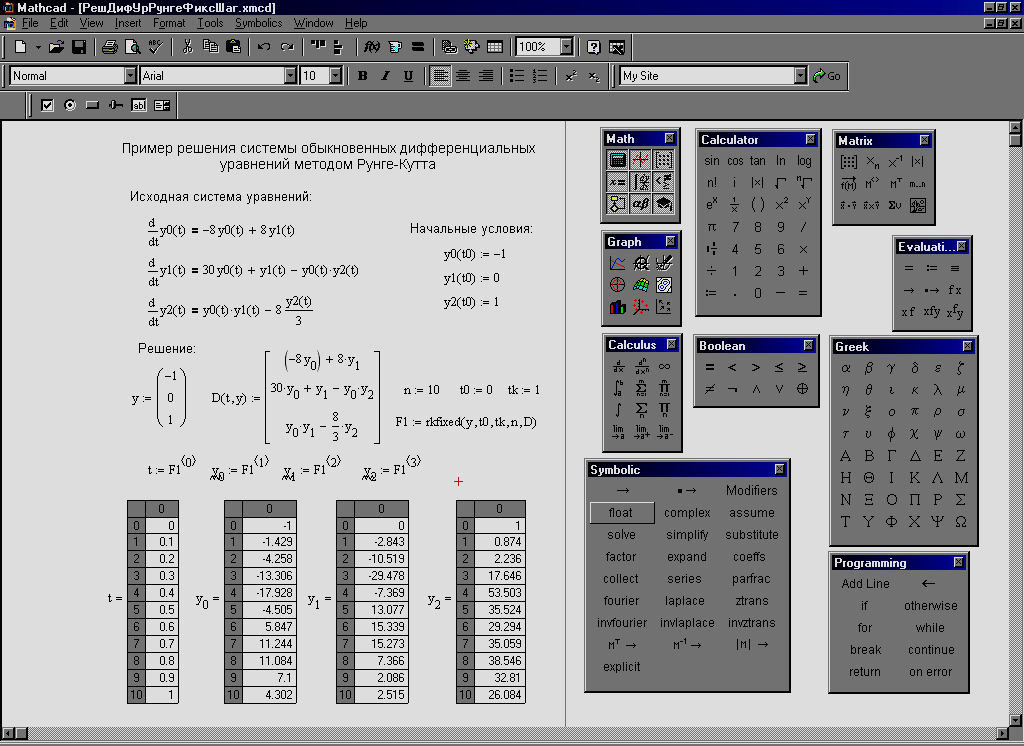
Рис. 4. Пример решения системы ОДУ функцией

rkfixed(y, x1, x2, npoints, D) и выводом решения в табличной форме

Решение системы уравнений представляет собой матрицу размерности (n+1)*npoits, поэтому для просмотра и оформления результатов необходимо аргументу t и искомым функциям присвоить значения соответствующих элементов векторов-столбцов матрицы решений S1 (интерполировать матрицу системой функций):

_{- значение вектора аргумента,}

- значение первой функции,

- значение второй функции, (3)

- значение n-й функции.