Вопрос 2.Магнитный поток. Работа по перемещению проводника с током в магнитном поле.

Магнитный поток – мера общего магнитного поля, проходящего сквозь заданную площадь. Измеряется в Веберах ([Ф]= Вб).

Густота силовых линий прямо пропорциональна модулю вектора индукции.

Если в неоднородное магнитное поле поместить площадку dS, в пределах которой магнитное поле считается однородным, то силовые линии пронизывают ее. В этом случае площадку dS пронизывает магнитный поток:

Полный магнитный поток сквозь произвольную поверхность:

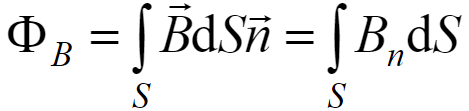
здесь B – вектор магнитной индукции, α – угол между вектором B и вектором нормали n к площадке dS.

На проводник с током в магнитном поле действует сила Ампера. В однородном магнитном поле:

где F = IℓB (сила Ампера).

Полную работу получим интегрированием

Работа работает не за счёт энергии магнитного поля, а за счёт источника тока. При изменении потока в контуре возникает ЭДС индукции Ԑ = – dФ/dt и работу можно записать

Билет №11.

Красный – доп. Информация.

1.

Коэффициенты этих линейных зависимостей называют емкостными коэффициентами, которые определяются размерами, формой и взаимным расположением проводников.

Если пространство между проводниками заполнено однородным диэлектриком, в котором нет свободных зарядов, то емкостные коэффициенты прямо пропорциональны его диэлектрической проницаемости.

В свою очередь, емкостные коэффициенты характеризуются следующими свойствами: 1) С_ij = С_ji; 2) С_ii  0 для всех i. Действительно, емкостные коэффициенты С_ij с одинаковыми индексами (i = j) положительны. Заземлим все проводники, кроме i-го, тогда q_i = C_ii_i. Но величины q_i и _i имеют одинаковые знаки. Следовательно, С_ii  0.

3) С_ij  0, если i  j, т. е. емкостные коэффициенты с различными индексами  отрицательны. Действительно, заземлим все проводники, кроме i-го и j-го. Сообщим i-му проводнику положительный заряд (q_i  0), а j-й  останется не заряженным (q_j = 0),а потенциалы _i и _j будут положительными.

Причем q_j = С_ji_i + C_jj_j = 0, что возможно, если С_ji  0. Во всех случаях потенциал поля в бесконечности равен нулю.

Просуммировав энергию каждого заряда можно получить энергию всей системы

dq =  dV, т. е. dW =  dq =   dV. С учетом этого предыдущая формула принимает вид

Если проводник имеет заряд q и потенциал  = const во всех точках, где распределен заряд, то

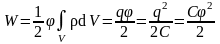
Так как для плоского конденсатора (два заряженных проводника) q = C , то

Тогда энергию электрического поля между обкладками плоского конденсатора можно найти, преобразуя предыдущую формулу с учетом того, что  = Е d, C = ε₀ ε S / d и V = S d:

Если поделить энергию заряженного конденсатора W на его объём V, то получим объёмную плотность энергии для электростатического поля (выражение получено из условий для однородного поля, но оно справедливо и для неоднородных полей)

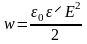
Возьмём выражение для энергии заряженного плоского конденсатора и продифференцируем его по направлению перпендикулярному плоскости обкладок

Мы получили силу, с которой обкладки конденсатора притягивают друг друг.

2. По определению, циркуляция вектора В равна:

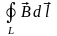
Вычислим этот интеграл для прямого тока. Пусть замкнутый контур лежит в плоскости рисунка, которая перпендикулярна току.

Итак, если ток в контуре, то циркуляция вектора B равна

Если ток вне контура, то

Вычислим индукцию магнитного поля внутри соленоида. Выберем прямоугольный контур таким образом, что две его стороны (длиной ℓ) параллельны оси соленоида, одна сторона совпадает с осью, вторая лежит за пределами соленоида. Две другие стороны перпендикулярны оси.

Циркуляция вектора B по данному контуру

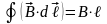
Контур охватывает суммарный ток

Согласно теореме о циркуляции вектора B, имеем Вℓ=₀NI.

Следовательно, индукция магнитного поля внутри соленоида В=₀nI,

Отсутствие в природе магнитных зарядов приводит к тому, что линии индукции вектора В не имеют ни начала ни конца. Поэтому поток вектора В сквозь замкнутую поверхность равен нулю (Теорема Гаусса)