
- •Введение
- •1. Теория множеств
- •1.1. Основные понятия
- •1.2. Операции над множествами
- •1.3. Алгебраические свойства операций над множествами
- •1.4. Нечёткие множества
- •2. Элементы комбинаторики
- •2.1. Основные правила комбинаторики
- •2.2. Выборки элементов без повторений
- •2.3. Выборки элементов с повторениями
- •2.4. Объединение комбинаторных конфигураций
- •2.5. Бином Ньютона
- •3. Отношения на множествах
- •3.1. Декартово произведение множеств
- •3.2. Булев куб и его свойства
- •3.3. Понятие отношения
- •3.4. Операции над отношениями
- •3.5. Свойства отношений на множестве
- •3.6. Отношения эквивалентности, толерантности и порядка
- •3.7. Нечеткие отношения
- •3.8. Понятие отображения
- •3.9. Алгебраическая операция
- •3.10. Общие сведения об алгебраических системах
- •4 Булевы функции
- •4.1. Основные определения и операции над высказываниями
- •4.2. Типы пф.
- •4.3. Равносильность формул
- •4.4. Дизъюнктивные и конъюнктивные нормальные формы
- •4.5 Алгоритм приведения пф к нормальным формам
- •4.6 Аналитический способ приведения к сднф
- •4.7. Табличный способ приведения к сднф
- •4.8. Табличный способ приведения к скнф
- •4.9. Логическое следствие
- •4.10. Алгоритм проверки правильности рассуждений
- •4.11. Алгоритм определения всех логических следствий из данных посылок
- •4.12. Алгоритм определения всех посылок, логическим следствием которых является данная формула
- •4.13. Полнота систем булевых функций
- •4.14. Полином Жегалкина
- •4.15. Замкнутость
- •4.16. Теорема Поста
- •4.17. Нечеткая логика
- •5. Многозначные функции
- •5.1. Функции и формулы k-значной логики
- •5.2. Полнота и замкнутость функций k-значной логики
- •5.3. Особенности k – значной логики
- •6.. Основные понятия теории графов.
- •6.1. Задачи теории графов.
- •6.2. Основные определения.
- •6.3. Степени вершин графа.
- •6.4. Изоморфизм графов.
- •6.5. Матричные способы задания графов.
- •6.6. Основные операции над графами.
- •6.7. Маршруты в графах
- •6.8. Связность в графах.
- •Связность и матрица смежности графа.
- •6.9. Матрица взаимодостижимости.
- •6.10. Деревья Свободные деревья.
- •Ориентированные, упорядоченные и бинарные деревья.
- •6.11. Эйлеровы графы.
- •6.12 Гамильтоновы графы.
- •6.13. Планарные графы.
- •6.14. Потоки в сетях. Основные определения.
- •Теорема Форда и Фалкерсона.
- •Алгоритм построения максимального потока в сети.
- •7. Конечные автоматы
- •7.1. Понятие конечного автомата Общие сведения о конечных автоматах
- •7.2. Абстрактное определение конечного автомата
- •7.3. Автоматная функция и её моделирование Понятие ограниченно детерминированной функции
- •Моделирование автоматной функции с помощью схемы из функциональных элементов и задержки
- •7.4. Эксперименты с автоматами
- •8. Рекуррентные уравнения
- •8.1. Определение рекуррентного уравнения/ Решение линейного однородного рекуррентного уравнения
- •8.2. Решение линейного неоднородного рекуррентного уравнения
- •8.3. Решение рекуррентного уравнения для чисел Фибоначчи
- •Заключение
- •Библиографический список
- •Оглавление
- •1.Теория множеств 5
- •2 Элементы комбинаторики 14
- •3 Отношения на множествах 22
- •4. Булевы функции 42
- •5. Многозначные функции 64
- •6. Основные понятия теории графов 70
- •7. Конечные автоматы 106
- •8. Рекуррентные уравнения 120
- •394026 Воронеж, Московский просп., 14
3.2. Булев куб и его свойства
Булев
вектор может применяться для моделирования
операций на конечных множествах. Пусть
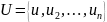 – некоторое универсальное множество
в рамках решаемой задачи. Элементы
множества для удобства помечены числовыми
индексами. Если
– некоторое универсальное множество
в рамках решаемой задачи. Элементы
множества для удобства помечены числовыми
индексами. Если
 ,
то множеству А
ставится
в соответствие n-
мерный булев вектор
,
то множеству А
ставится
в соответствие n-
мерный булев вектор
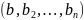 ,
в котором
,
в котором
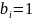 ,
если
,
если
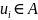 и
и
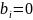 в противном случае. Такая строка бит
называется характеристическим
вектором
множества А.
При этом, операции на множествах
имитируются соответствующими логическими
операциями на характеристических
векторах.
в противном случае. Такая строка бит
называется характеристическим
вектором
множества А.
При этом, операции на множествах
имитируются соответствующими логическими
операциями на характеристических
векторах.
Для размерности n операции над векторами производятся покоординатно. Логическая сумма двух векторов – вектор, координаты которого являются логическими суммами соответствующих исходных векторов. Аналогично определено произведение.
Между
множеством всех подмножеств множества
U
и булевым кубом
,
где
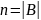 можно установить взаимнооднозначное
соответствие, при котором операции
объединения множества соответствует
операции логического сложения (их
характеристических векторов), операции
пересечения множеств соответствует
операция логического умножения их
характеристических векторов, а операции
дополнения – операция отрицания. Пустому
множеству соответствует нулевой вектор,
а универсальному – единичный.
можно установить взаимнооднозначное
соответствие, при котором операции
объединения множества соответствует
операции логического сложения (их
характеристических векторов), операции
пересечения множеств соответствует
операция логического умножения их
характеристических векторов, а операции
дополнения – операция отрицания. Пустому
множеству соответствует нулевой вектор,
а универсальному – единичный.
Пример.
Пусть
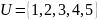 ,
,
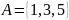 и
и
 .
Характеристическими векторами множеств
А,
В,
.
Характеристическими векторами множеств
А,
В,
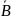 ,
,
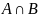 и
соответственно будут:
и
соответственно будут:
 .
Полученные векторы позволяют легко
выписать элементы множеств:
.
Полученные векторы позволяют легко
выписать элементы множеств:
 .
.
Номером булевого вектора называется число его двоичного представления. Например, булев вектор а из предыдущего примера имеет номер 10101.
Два булевых вектора называются соседними, если их координаты отличаются только в одном разряде (т.е. они отличаются только одной координатой).
Булев куб размерности 1

Рис. 9
Булев куб размерности 2
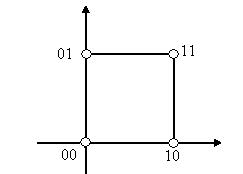
Рис. 10
Булев куб размерности 3
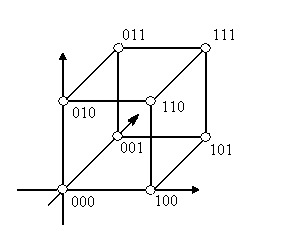
Рис. 11
3.3. Понятие отношения
Для выражения взаимодействий и связей между элементами множеств в математике используется понятие отношения.
n
– местным (n
– арным) отношением
R
на множествах
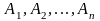 называется
любое подмножество прямого произведения
этих множеств, то есть
называется
любое подмножество прямого произведения
этих множеств, то есть
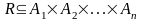 .
Другими словами, элементы этих множеств
.
Другими словами, элементы этих множеств
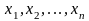 связаны
отношением R
тогда и только тогда, когда n
упорядоченных чисел
связаны
отношением R
тогда и только тогда, когда n
упорядоченных чисел
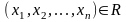 .
.
Отношение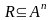 называется n
– местным
на множестве А.
называется n
– местным
на множестве А.
При
 отношение R
задает фиксированный элемент множества
А.
При
отношение R
задает фиксированный элемент множества
А.
При
 отношение R
представляет собой подмножество
множества А
и называется унарным
отношением
или свойством.
При
отношение R
представляет собой подмножество
множества А
и называется унарным
отношением
или свойством.
При
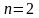 отношение R
называется бинарным
или
соответствием.
При
отношение R
называется бинарным
или
соответствием.
При
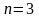 отношение тернарное
и т. д.
отношение тернарное
и т. д.
В математике чаще всего используются бинарные отношение (соответствия). В дальнейшем рассматриваются в основном только такие отношения и при этом слово “бинарные” опускается.
Пусть
А и
В
– два множества. Соответствием
или (бинарным)
отношением
из множества А
в множество В
называется подмножество R
прямого произведения
,
т.е.
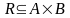 .
Если aA,
bB,
находятся в отношении, то пишут: (a,b)R
или R(a,b),
а также в инфиксной форме aRb.
При этом говорят, что b
соответствует a
при соответствии R
или b
находится в отношении R
с a.
Если R=,
то отношение называют пустым.
Отношение
.
Если aA,
bB,
находятся в отношении, то пишут: (a,b)R
или R(a,b),
а также в инфиксной форме aRb.
При этом говорят, что b
соответствует a
при соответствии R
или b
находится в отношении R
с a.
Если R=,
то отношение называют пустым.
Отношение
 называют полным.
Для любого множества А
определяется тождественное
отношение
-
называют полным.
Для любого множества А
определяется тождественное
отношение
-
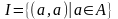 .
.
Принадлежность элементов а и b отношению R наглядно можно представить в следующем виде
 Рис.
12
Рис.
12
Областью определения (DomR) соответствия R, называется множество элементов aA, для каждого из которых, найдется хотя бы один элемент bB, такой, что aRb.
Областью значения (ImR) соответствия R называется множество элементов bB, для каждого из которых, найдется хотя бы один элемент aA, такой, что aRb.
Соответствие R называется всюду определенным, если DomR=A, в противном случае – частично определенным. Соответствие называется сюръективным, если ImR=B.
Для каждого aA, множество элементов bB таких, что aRb называется образом элемента aA относительно R и обозначается imRa.
Прообразом элемента bB относительно R, называется множество элементов aA, таких, что aRb. Прообраз обозначается: coimRb
Заметим,
что
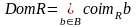 и
и
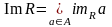 .
.
В общем случае отношения (соответствия) могут быть заданы любым из двух способов, которые используются для задания множеств, т.е. перечислением элементов отношения или указанием их характеристических свойств.
Отношения,
определенные на конечных множествах
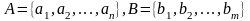 ,
могут быть заданы:
,
могут быть заданы:
Списком, т.е. перечислением тех пар элементов, для которых это отношение выполнено. Например, если A={a,b,c} и B={x,y}, то R={(a,x),(a,y),(b,y),(c,x)}.
Матрицей [R] размерности , элементы которой
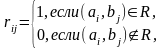 т.е. строки этой матрицы помечаются
элементами из A,
а столбцы – элементами из B,
а на пересечении строки ai
со столбцом bi
стоит единица (1), если aRb;
и нуль (0), - в противном случае. Тогда
для выше приведенного примера имеем
матрицу
т.е. строки этой матрицы помечаются
элементами из A,
а столбцы – элементами из B,
а на пересечении строки ai
со столбцом bi
стоит единица (1), если aRb;
и нуль (0), - в противном случае. Тогда
для выше приведенного примера имеем
матрицу
Таблица 6
|
x |
y |
a |
1 |
1 |
b |
0 |
1 |
c |
1 |
0 |
Г
 рафиком
на координатной плоскости, горизонтальная
и вертикальная оси которой представляют
элементы множеств А
и В
соответственно.
рафиком
на координатной плоскости, горизонтальная
и вертикальная оси которой представляют
элементы множеств А
и В
соответственно.
Рис. 13
Графом, в котором элементы множеств А и В изображаются точками на плоскости. Причем эти точки обозначаются теми же символами, что и соответствующие элементы. Точки a и b соединяются направленным отрезком от a к b, если aRb. Например, для предыдущего случая отношение R изображается ориентированным графом.
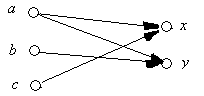
Рис. 14
