5. Многозначные функции
Конечнозначная логика вводится как обобщение двузначной логики. Она используется для описания функционирования сложных управляющих систем. Компоненты этих систем могут находиться в конечном числе состояний.
5.1. Функции и формулы k-значной логики
Функция
,
аргументы и значения, которой определены
на множестве истинностных значений
,
называется функцией k-значной
логики.
Каждую
функцию k-значной
логики от n
– аргументов можно задать в виде таблицы
содержащей
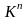строк.
Таблица 15
|
|
0 0 0 |
|
0 0 1 |
|
. . . . . . . . . . . . . . . . |
. . . . . . . . . . |
0 0 k-1 |
|
0 1 0 |
|
. . . . . . . . . . . . . . . . |
. . . .. . . . . . . |
0 k-1 k-1 |
|
Множество
всех функций k-значной
логики обозначается
(
).
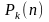Заметим, что
.
В частности число функций от двух
переменных в
равно
=19683,
т.е. это множество практически
не обозримо. Поэтому в
так же как и в
,
используется задание функций с помощью
формул. В качестве «элементарных» в
k-значной
логике рассматриваются следующие
функции:
`
.
Эта функция представляет собой отрицание в смысле «циклического сдвига значений».
– это
обобщение отрицания в смысле «зеркального
отображения значений». Оно носит
название отрицание
Лукашевича.
.
Эта функция также является обобщением некоторых свойств отрицания.
.
Это характеристическая функция значения i, которая также обобщает отрицание.
– это
обобщение конъюнкции.
– это
есть второе обобщение конъюнкции.
– обобщение
дизъюнкции.
– второе
обобщение дизъюнкции.
Используя
переменные, допустимые значения которых
являются элементы множества
и символы некоторых функций из
можно строить формулы, которые задают
функции из
.
Любая функция из может быть представлена в виде:
,
где под конъюнкцией понимается
,
а под дизъюнкцией
.
В этом выражении дизъюнкция распространяется
по всем наборам
элементов
.
Данное представление является аналогом СДНФ.
5.2. Полнота и замкнутость функций k-значной логики
Система
функций из
(
)
называется (функционально) полной,
если любая функция из
может быть записана в виде формулы через
функции этой системы.
Примерами полных систем является:
= .
=
.=
.=
,где
.
Функция
называется фуннцией
Вебба
представляет собой аналог функции
Шеффера.
Пусть – произвольное подмножество функции из . Замыканием называется множество [] всех функций из , представленных в виде формул через функции множества `
Класс называется (функционально) замкнутым, если замыкание []=.
Таким образом, в терминах замыкания можно определить полноту системы функций, а именно является полной системой если замыкание []= .
Справедлива теорема о функциональной полноте - теорема Кузнецова А.В.:
Можно построить систему замкнутых классов в - 1, 2,…,s, каждый из которых не содержит целиком ни одного из остальных классов и такую, что подсистема функций из полна тогда и только тогда, когда она целиком не содержится ни в одном из классов 1, 2,…,s. Это аналог теоремы Поста.
Теорема Кузнецова доказывает, что возможно выразить, условие полноты системы в терминах принадлежности ее к специальным классам 1, 2,…,s, однако практическое построение классов даже при небольших k связано с трудоемкими вычислениями. Поэтому возникает вопрос о поиске других более эффективных критериев полноты. Эта цель достигается за счет введения ограничений , т.е. за счет знания дополнительной информации о системе .
Существенными
называются функции
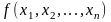из
,
если они существенно зависят не менее
чем от двух переменных.
Теорема Яблонского
Пусть система функций из , где k ³ 3, содержит все функции одной переменной, принимающие не более k-1 значений. Тогда для полноты системы необходимо и достаточно, чтобы содержало существенную функцию , принимающую все k значений.
Следствие (критерий Слупецкого):
Пусть система функций из , где к ³ 3, содержит все функции одной переменной. Тогда для полноты системы необходимо и достаточно, чтобы содержало существенную функцию , принимающую все k значений.
Непосредственное
использование теоремы и ее следствия
не всегда удобно, так как для этого
необходимо установить наличие в
всех функций одной переменной, принимающих
не более k-1
значения, т.е.
функций. С ростом k
громоздкость вычислений возрастает.
Поэтому это требование целесообразно
заменить требованием, в котором система
функций
порождало бы множество функций одной
переменной.
Известно, что функции из могут быть получены из конкретных систем функций одной переменной.
Теорема 1 (Пикара).
Все функции одной переменной из могут быть порождены тремя функциями:
,
,
.
Теорема 2
Все функции одной переменной из могут быть порождены k функциями
и
функцией
.
Теорема 3 (Мартина).
Функция из при к ³ 3 является функция Шеффера, тогда и только тогда, когда порождает все функции одной переменной принимающие не более k-1 значений.