Министерство образования

РОССИЙСКОЙ ФЕДЕРАЦИИ

Воронежский государственный технический университет

Кафедра робототехнических систем

Алгоритмы адаптивного уровня управления робота

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к лабораторным работам № 4, 5

по дисциплине "Управление роботами и РТС"

для студентов специальности 210300

"Роботы и робототехнические системы"

очной и очно-заочной (вечерней) форм обучения

Воронеж 2004

Составитель канд. Техн. Наук в.А. Медведев

УДК 519.71

Алгоритмы адаптивного уровня управления робота: Методические указания к лабораторным работам № 4, 5 по дисциплине “Управление роботами и РТС” для студентов специальности 210300 “Роботы и робототехнические системы” очной и очно-заочной (вечерней) форм обучения / Воронеж. гос. техн. ун-т; Сост. В.А. Медведев. Воронеж, 2004. 36 с.

Методические указания содержат теоретические сведения о методе конечно-сходящихся алгоритмов и его применении для планирования движения мобильного робота, математическом описании двухкоординатного манипулятора и самонастраивающейся системы управления. Сформулированы пред­варительное и рабочее задания на лабораторные работы, требования к содержанию отчетов и контрольные вопросы.

Методических указаний предназначены для студентов 5 курса очной и 6 курса очно-заочной (вечерней) форм обучения специальности 210300 “Роботы и робототехнические системы”. Они будут полезны студентам при выполнении лабораторных работ, углубленном изучении лекционного материала, курсовом и дипломном проектировании.

Методические указания подготовлены на магнитном носителе в текстовом редакторе Microsoft Word 97 и содержатся в файле met45.doc.

Табл. 2. Ил. 5. Библиогр.: 9 назв.

Рецензент канд. Техн. Наук, доц. М.И. Герасимов Ответственный за выпуск зав. Каф. Рс д-р техн. Наук проф. А.И. Шиянов

Издается по решению редакционно-издательского совета Воронежского государственного технического университета с Воронежский государственный технический университет, 2004

Л абораторная работа № 4

Планирование движений мобильного робота

1. Цель работы

Целью работы является изучение алгоритма построения программных движений мобильного робота с учетом препятствий на основе метода конечно–сходящихся алгоритмов, а также исследование влияния граничных условий и величины области запрещенных значений на форму планируемых траекторий манипулятора и транспортной тележки.

2. Теоретические сведения

В условиях мелкосерийного и серийного машиностроительного производства целесообразно создание гибкой производственной системы (ГПС), которую можно быстро перенастраивать при изменении технологического процесса, числа партий выпускаемых деталей и их номенклатуры.

Оборудование ГПС обычно включает в себя один или несколько складов, основное и вспомогательное технологическое оборудование, связанные транспортной системой, которая обеспечивает производственную систему заготовками (сырьем), оснасткой, инструментами, транспортирует отходы и готовую продукцию, а также обслуживает оборудование для контроля продукции.

В состав транспортной системы целесообразно включать мобильные роботы, которые соответственно текущим потребностям многономенклатурного производства способны изменять свой маршрут, обеспечивая подвоз кассет с деталями к требуемому станку. За счет этого сокращается время простоя станков, обработавших очередную партию деталей, и повышается общий коэффициент использования оборудования.

По сравнению с конвейерными системами, транспортные системы, обслуживаемые мобильными роботами, легче устанавливать, значительно проще расширять, сокращать или модифицировать маршруты обслуживания.

В память бортовой ЭВМ робота заносятся координаты всех препятствий в цехе, которыми являются станки, технологическое оборудование и др. Затем задается целевое условие – координаты конечной точки. Бортовая ЭВМ рассчитывает траекторию движения с учетом ограничений по скорости, положению и параметров препятствий. Рассчитанная траектория хранится в памяти робота до получения следующего целевого условия, а также передается в банк траекторий центральной ЭВМ. За счет оперативного перехода на новые маршруты простои оборудования занимают минимальное время.

Планирование движений манипулятора, установленного на мобильном роботе, позволяет исключить трудоемкий процесс обучения. Производство становится более гибким, автономным, уменьшаются простои оборудования.

2.1. Общий подход к построению программных движений робота

Законы изменения обобщенных координат при программном движении (ПД) должны удовлетворять следующим требованиям:

в процессе движения все звенья манипулятора и тележка не задевают препятствий;

выполнены конструктивные ограничения на обобщенные координаты;

движения манипулятора и тележки достаточно плавные.

Задача расчета требуемых траекторий на основе полученной от центральной ЭВМ информации об опорных точках, через которые мобильный робот должен следовать, может быть решена путем интерполяции траектории между опорными точками с помощью сплайн-функций. Однако, при этом игнорируются ограничения на перемещения робота, связанные с препятствиями, а также динамические ограничения, присущие исполнительному механизму робота. В то же время учет этих ограничений необходим с точки зре­ния принципиальной осуществимости и эффективности синтези­руемых ПД.

Программное движение 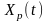при всех 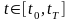должно удовлетворять следующим конструктивным и динами­ческим ограничениям [1]:

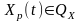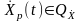, , (1)

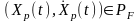, (2)

где 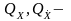заданные ограниченные области в n-мерном пространстве;

P_F – подпространство в 2n-мерном пространстве, вид которого определяется уравнением движения

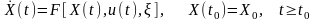, (3)

где 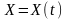– n - мерный вектор состояний исполнительных приводов и механизмов в текущий момент времени t;

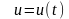– m - мерный вектор управлений;

 – р - мерный вектор параметров двигательной системы;

– начальное состояние.

Кроме того, ПД должно удовлетворять заданным граничным условиям

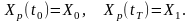(4)

Отметим также, что ПД как частное решение уравнения движения (3) при некотором допустимом управ­лении 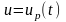зависит от параметров 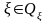. В задачах про­граммного управления предполагается, что эти параметры известны. В рассматриваемом случае на класс ПД накладываются более жесткие ограни­чения, связанные с учетом структуры множества 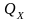состояний.

Построение ПД осуществляется с учетом свойств динамической модели ро­бота с гранич­ными условиями (4) и ограничениями (1) (2). Эффективным методом синтеза ПД является метод их параметризации с учетом гранич­ных условий (4) [2, 3]. Этот метод обеспечивает отыскание приемлемых пара­метров ПД при выполнении граничных условий (4) и учете динамического ограничения (2), что достигается путем специального выбора базисных функций.

Рассмотрим подробно один из вариантов метода параметри­зации ПД [3, 4]. Будем искать ПД в многопараметрическом классе функций вида

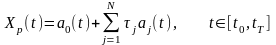. (5)

где 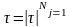– вектор искомых параметров;

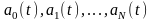– заданные N - мерные вектор - функции. Будем назы­вать их базисными, если они удовлетворяют следующим усло­виям [2, 3]:

1) функции 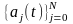таковы, что ПД (3) удовлетворяет граничным условиям (4) при любом выборе параметров ₁, ..., _N;

2) функции и их производные 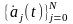попарно удовлетворяют структурному ограничению 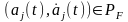при всех ;

3) функции при любом конечном числе N линейно независимы;

4) каковы бы ни были функция 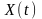на интервале [t₀, t_T] и положительное число , существует натуральное число N и постоянные коэффициенты 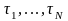такие, что

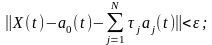(6)

5) функции достаточно просты для программной или схемной реализации.

Перечисленные требования к базисным функциям имеют следующий смысл. Первое требование обеспечивает решение двухточечной краевой задачи, второе гарантирует осуществимость параметризованного ПД (5) с учетом динамики робота, третье и четвертое означают возможность экономного и вместе с тем сколь угодно точного представления ПД в виде (5) и, наконец, пятое обеспечивает простоту технической реализации искомого ПД.

Первая задача в рамках параметрического метода построения ПД заключается в рациональном выборе базисных функций. Рассмотрим некоторые примеры и общие рекомендации по конструированию базисных функций.

Базисными функциями, удовлетворяющими сформулированным требованиям, могут служить полиномы

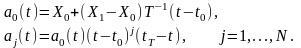(7)

В самом деле, при таком выборе базисных функций ПД (5) удовлетворяет граничным условиям (4), динамическому ограничению (2), а также требованиям точной аппроксимации и простой реализации.

Другим примером рационального выбора базисных функций являются тригонометрические многочлены

(8)

,

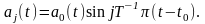
При конструировании базисных функций можно руководствоваться следующим правилом: в качестве функции 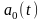выбирать непрерывно дифференцируемую вектор-функцию, удовлетворяющую граничным условиям (4), а в качестве остальных базисных функций - функции вида

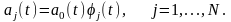(9)

Здесь _j(t) – числовые функции на временном интервале [t₀, t_T], удовлетворяющие однородным граничным условиям, т. е.

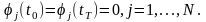(10)

В качестве _j(t) можно выбирать рассмотренные полиномы и тригонометрические многочлены.

Большой интерес представляет также такая параметризация ПД, когда в качестве функций _j(t) берутся сплай­ны [5, 6], т.е. кусочно-полиномиальные функции со следую­щими свойствами:

1) существует разбиение 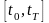на подынтервалы, такое, что внутри каждого подынтервала _j(t) представляет собой много­член степени r;

2) функции _j(t) непрерывны вместе с производными до (r-1)-го порядка и имеют интегрируемую с квадратом произ­водную порядка r на интервале .

Конструирование базисных функций с учетом высказанных соображений обеспечивает соблюдение граничных условий (4), динамического ограничения (2) при любом выборе параметров ₁, ..., _N в функции (5), а также приводит к высокой точности аппроксимации и простой реализации синтезируемых ПД. После выбора базисных функций a₀(t), a₁(t), ...,a_N(t) можно перейти к фактическому построе­нию ПД вида (5).

Задача синтеза программных движений сводится к отыска­нию приемлемых значений параметров ₁, ..., _N. Эти пара­метры следует определять исходя из заданных ограничений (1), где 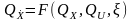. Ограничения (1) с учетом (5) превращаются в систему не­равенств относительно параметров .

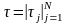Таким образом, задача построения ПД в результате параметризации (5) сводится к решению системы неравенств, описывающих ограничения (1), относительно параметров искомого ПД.

Для решения полученных неравенств про­стым и эффективным является метод, использующий рекуррентные конечно-сходящиеся алгоритмы [7] решения нера­венств.

2.2. Конечно-сходящиеся алгоритмы решения рекуррентных неравенств

Введем искомый вектор подстраиваемых параметров . Пусть t = 0, 1,..., t-1 дискретное время, _t(), _t() – вещественные функции. Предположим, что имеется некоторое правило, сопоставляющее каждому набору 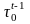векторов [_0, _{1, ...,} _t-1], составляющие которого соответствуют значениям вектора  в дискретные моменты времени, две функции от  :

(11)

(Далее, для краткости, аргументы у этих функций не выписываются.)

Рассмотрим неравенства

(12)

которые будем называть условными неравенствами, и не­равенства

(13)

которые будем называть безусловными неравенствами.

В задачах адаптивного управления неравенства (12) порождаются целевым условием (целью управления); неравенства (13) описывают ограничения на возможные значения вектора 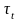подстраиваемых параметров. Знаки  или > в (12), (13) в каждый момент времени могут быть любыми. Неравенства (13) в частном случае могут отсутствовать.

Пусть заданы множество {}° начальных значений вектора ₀ подстраиваемых параметров и правило

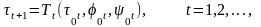(14)

сопоставляющее набору 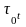и наборам функций

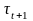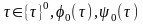значение . Тогда для заданных последовательно определяются 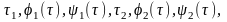и т. д. Неравенства (12), (13) заранее для всех t не заданы, они появляются последовательно во времени после очередного «срабатывания» алгоритма (14). Поэтому будем называть (12) и (13) рекуррентными неравенствами. Для разных алгоритмов (14) неравенства (12) и (13) будут разными. Правая часть (14) обычно зависит лишь от .

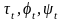Уравнение (14) является конечно-сходящимся алгоритмом (КСА) решения рекуррентных неравенств – условных (12) и безусловных (13), если для всех t выполнено (13) при и если существует такой момент времени t^*, что для t  t^* выполняются неравенства (12) при и векторы _t не изменяются: 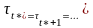. Число r моментов времени t  1, для которых при не выполняется (12), называется числом ошибок (коррекций) алгоритма.

Итак, КСА – алгоритм, доставляющий решение бес­конечного числа заранее незаданных условных рекуррентных неравенств: неравенства (12) при t < t^* могут остаться невыполненными. На каж­дом шаге решение должно выбираться из области, опре­деляемой также появляющимся рекуррентным неравенством.

Важно помнить, что рекуррентные неравенства (12), (13) могут зависеть от алгоритма (14): для разных алгоритмов они разные.

При решении задачи построения КСА требуется за конечное время найти решение бес­конечной системы неравенств, заранее неизвестных. Однако, многие задачи адаптации приводят к рекуррентным неравенствам, для которых выполнен ряд дополнительных свойств, что дает возможность строить такие алгоритмы. Наличие определенной стабильности, присущей обычно практическим задачам, приводит к тому, что неравенства (12), (13) выполняются для всех t при значениях подставляемых параметров из некоторой окрестности вектора 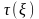. Иначе, для эти неравенства выполнены «с запасом». Второе важное свойство, которое часто имеет место, – это наличие областей в пространстве {}, определяемых рекуррентными неравенствами (12), (13). Указанные два обстоятельства позволяют строить КСА следующим образом.

Пусть безусловные неравенства отсутствуют. Обозначим через Т_t область, определяемую неравенством (12). Если (12) выполняется для , т.е. 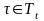то полагаем 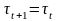. Если (12) не выполнено для , то существует плоскость П_t, отделяющая вектор _t от множества Т_t. Выберем в качестве _t+1 ортогональную проекцию вектора _t на плоскость П_t. Вектор _t+1 будет ближе к неизвест­ному нам вектору (), чем _t. Из сделанных предположений следует существование такого не зависящего от t числа  > 0, что

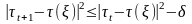. (15)

Итак, построенный алгоритм будет обладать свойством (15). Отсюда следует его конечная сходимость. Каждый раз, когда не выполнено (12), справедливо (15), т. е. величина 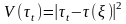убывает по меньшей мере на . Когда неравенство (12) выполнено, то V(_t ) не изменяется. Поэтому число r ошибок алгоритма конечно.

Плоскость П_t можно строить по-разному: при этом получаются различные КСА. Вместо функции 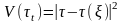можно выбрать любую неотрицатель­ную функцию; важно лишь, чтобы для некоторого  > 0 выполнялось

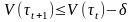при ()<0 (0). (16)

2.3. Конечно-сходящийся алгоритм «Полоска-1»

Рассмотрим следующую систему условных рекуррентных неравенств в пространстве {}:

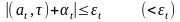, (17)

где t = 0, 1, 2, ...; a_t  {};

(а_t, ) – скалярное произведение векторов а_t и  ;

_t, _t – вещественные числа.

Запись (<_t) в (31) означает, что вместо | . . . |  _t для некоторых t (в частности, для всех t) может быть | . . . | <_t. Относящиеся к этому случаю изменения также будут записаны в скобках (...).

Неравенство (17) для фиксированного t определяет полосу между двумя параллельными плоскостями в про­странстве {}. Полосы (17) по смыслу решаемой задачи могут быть заранее неизвестны: предполагается задан­ным некоторый алгоритм, доставляющий по значениям ₀, ...,_t вектор a_t  {} и числа _t,_t.

Будем предполагать выполненными следующие усло­вия:

а) существует такое  > 0, что для любого t  0

, (18)

б) существуют вектор _* и число  (0   < 1), такие, что при всех t  0 выполняется неравенство

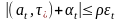. (19)

Пусть выполняются условия а) и б). Введем обозначение:

. (20)

Пусть — произвольное число, > min (1, 2). Для про­извольного ₀ следующий КСА решает условные неравенства (12) (по теореме 2.1.1 [8]):

(21)

Заметим, что условие в скобках в (21) относится к случаю, когда в (17) знак «меньше».

Геометрическая интерпретация формул (21) приведена на рис. 1. Через _t обозначено: .

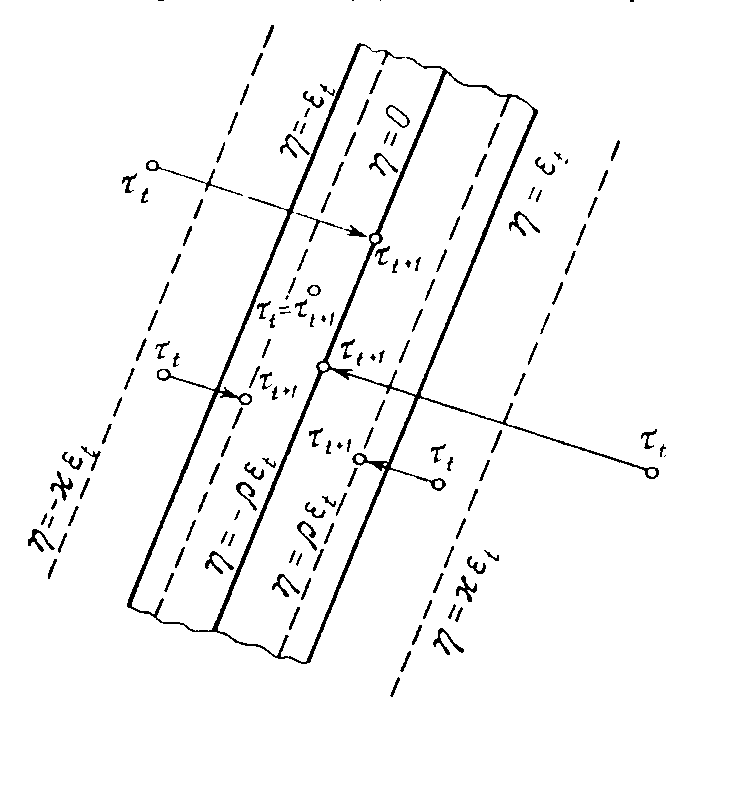
Рис. 1. Геометрический смысл алгоритма «Полоска - 1»

Если точка  _t находится в полосе (19), то . Если _t лежит вне полосы 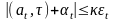, то точка _t+1 получается из _t проектированием на «сред­нюю плоскость» полосы (17), т.е. на плоскость 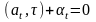. Если же _t находится «близко» к полосе (17) (именно, если _t <| _t| < _t), то точка _t+1

получается проектированием _t на ближайшую из плоскостей .

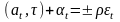Вектор _t+1 всегда лежит в полосе (17). Таким образом, алгоритм (21) можно применять для решения безусловных рекуррентных неравенств, если только неравенство (17) относится к моменту вре­мени t+1, т.е. если в соответствии с обозначениями п. 2.2 неравенство (17) имеет вид .

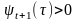В частном случае можно взять = , тогда второй случай в (21) будет всегда отсутствовать и алгоритм (21) примет вид:

(22)

Алгоритм предполагает знание числа , определяющего «запас» выполнения неравенств для некоторого =_* .

Если  < 1/2, то можно взять <1; в этом слу­чае алгоритм (21) приобретает особенно простой вид

(23)

Геометрическая интерпретация алгоритма (23) состоит в следующем: значение _t+1 совпадает с _t, если выполнено условие (17), и получается из _t проектированием на плоскость в противном случае.

Алгоритм, доставляющий значения a_t, _t, _t, может быть и таким, что эти значения зависят лишь от t, в этом случае неравенства (17) по существу заданы заранее; каждый из алгоритмов (21) (23) доставит через конечное число шагов решение всего бесконечного «хвоста» этих неравенств. В особенно простом случае неравенства (17) получаются циклическим повторением заданной конечной системы неравенств (т.е. a_t+T=a_t, _t+T=_t, _t+T=_t для некоторого натурального Т). Таким образом, каждый из алгоритмов (21) (23) мо­жет быть использован для решения конечной заданной системы неравенств, представленных в виде (17).

Алгоритм «Полоска-1» позволяет рассчитывать программные задания на движение мобильного робота в зоне, свободной от препятствий, за достаточно короткий интервал времени.

2.4. Построение программных движений самоходной тележки

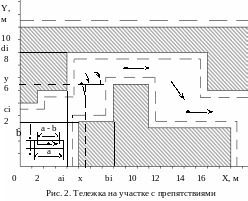
Рассмот­рим задачу построения ПД тележки, передвигающейся по цеху с препятст­виями (см. рис. 2).

Положение тележки на плоскости 0XY определяется вектор - функцией

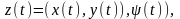(24)

где x(t), у(t) – текущие значения координат центра масс тележки;

(t) – текущее значение курсо­вого угла тележки.

Программным движением z_p(t) ( t  [t₀, t_T]) транспортной тележки будем называть такое ее допустимое движение, которое обеспечивает переход робота из произвольного начального состояния z(t₀), (t₀) в желаемое конечное состояние z(t_T), (t_T), при котором выполняется целевое условие.

Препятствия аппроксимируем на плоскости 0XY с помощью прямоугольников, координаты которых записываются в память робота. В этом случае прямоугольные зоны, свободные от препятствий, характеризуются параметрами а_i, b_i, с_i, d_i. Для обеспечения движения центра масс тележки без столкновения с препятствиями должны быть выполнены условия:

если а_i< x < b_i, то c_i<y<d_i при всех i. (25)

Окружим препятствия такой 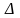- окрестностью, чтобы достаточно было следить не за движе­нием всей тележки, проекция которой на плоскость ОХY имеет форму прямоугольника, а только за имитирующим ее вектором длины (с модулем l=|а-b|), проходя­щим через центр масс тележки с тем же курсовым углом. Величину можно взять равной 1/2 min (а, b), где а и b – длины сторон проекции тележки.

Функцию изменения курсового угла будем искать в виде полинома

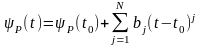. (26)

где _р(t₀) – начальное значение курсового угла;

b_j – искомые параметры движения.

Для обеспечения плавности движения по координате  достаточно применять кубический полином, т.е. N=3.

Примем для простоты, что движение центра масс тележки вдоль оси 0X равномерное. Координата x_p(t) центра масс определяется в этом случае из выражения:

t[t₀, t_T], (27)

где x_р(t₀) и x_р (t_T) – начальное и конечное значения координаты x центра масс тележки;

Т– период времени движения.

Программное движение центра масс тележки вдоль оси 0Y определяется интегральной зависимостью:

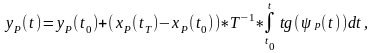(28)

где y_р(t₀) – начальное значение координаты y центра масс тележки.

ПД тележки, выбранное в классе функций (26)(28), обеспечивает перемещение тележки в направлении, соответствующем курсовому углу _р(t). Параметры b_j (j=1, ... N) полинома вида (26) необходимо выбрать так, чтобы удовлетворить условиям (25) обхода препятствий.

Текущим значениям t и (t) соответствуют x_р(t, (t)) и y_р(t, (t)), вычисляемые из (27), (28). При этом для i-ой свободной от препятствий прямоугольной зоны, определяемой из условия а_i < x_р(t, (t)) < b_i для координаты y_р(t, (t)) согласно (25) должно выполняться нера­венство c_i < y_р(t, (t)) < d_i. Для определения параметров b_j, обеспечивающих выполнение этих неравенств, использует­ся конечно-сходящийся алгоритм «Полоска-1» [7], описанный в предыдущем пункте и доставляющий через конечное число коррекций искомое реше­ние.

2.5. Построение программных движений манипулятора

Для проведения погрузочно-разгрузочных работ в цехе мобильному роботу достаточно иметь манипулятор с цилиндрической системой координат и с тремя основными степенями подвижности.

Конфигурация (положение) манипулятора мобильного робота в момент времени t однозначно определяется вектором обобщенных координат (степеней свободы) q(t)=|q_j(t)|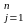 или вектором s(t)=|s_i(t)|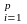 , компонентами которого являются декартовы координаты концов звеньев манипулятора. Между вектор функциями q(t) и s(t) существует взаимно-однозначное непрерывное соответствие, т. е. существует функция s(t)= Ф[q(t)] для любого t  t₀. Движе­ние манипулятора однозначно определяется функциями q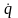(t), (t).

Программным движением манипулятора мобильного робота q_р(t), t[t₀, t_T] будем называть такое его допустимое движение, которое обеспечивает переход схвата из произвольного начального состояния q(t₀), (t₀) в желаемое конечное состояние q(t_T), (t_T), при котором выполняется целевое условие.

С точки зрения построения траекторий, обеспечивающих огибание препятствий (станков), наиболее интересны вертикальное и горизонтальное движения манипулятора.

Н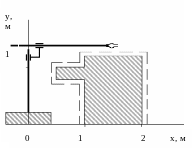 а рис. 3 изображен манипулятор, установленный на транспортной тележке, препятствие и система ортогональных координат 0xy.

Рис. 3. Манипулятор мобильного робота

Положение конца схвата манипулятора определяется в момент времени t формулами:

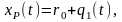(29)

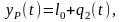(30)

где x_p(t), у_p(t) – координаты схвата манипулятора;

r₀, l₀ – конструктивные параметры манипулятора.

При движении манипулятора, представленного на рис. 3, отсутствие касания схвата о препятствие означает, что и все другие точки манипулятора не будут сталкиваться с препятствием.

Препятствие аппроксимируем прямоугольниками, стороны которых параллельны координатным осям, и окружим -областью. Величина  выбирается в зависимости от размеров кассеты с деталями, которую должен переместить манипулятор. Параметры препятствий заносятся в массив чисел {а_i, b_i, с_i, d_i}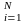 таких, что выполнены условия:

если c_i< y <d_i , то а_i< x < b_i при всех i. (31)

В данном случае неравенства (31) должны быть выполнены для точки в центре схвата с координатами x_P(t), y_P(t) при каждом t[t₀, t_T].

Примем для упрощения решения задачи движение y_р(t) вдоль оси 0у равномерным:

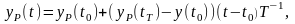(32)

где y_р(t₀) и y_р(t_Т) – начальное и конечное состояния по координате 0у;

Т – время выхода в заданное положение по оси 0у.

Движение х_р(t) вдоль оси 0х будем искать в виде полинома:

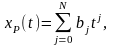(33)

где b_j – искомые параметры ПД.

Определим параметры препятствий такие, что c_i<y_р^(к)<d_i. Тогда для координаты 0х должны выполняться неравенства а_i< x_р^(к) < b_i при всех i, которые линейны относительно неизвестных коэффициентов полинома (33). Система полученных линейных неравенств, порожденных препятствиями, разрешима, если только целевое условие вообще выполнимо в рассматриваемом классе движений (33). Применяя для решения полученной системы неравенств конечно - сходящийся алгоритм «Полоска-1» (явные формулы которого приведены в п. 2.3), получим после конечного числа коррекций искомые значения параметров b_j ПД вида (33). Полученное ПД, определяемое неравенствами (32), (33), достаточно плавное и удо­влетворяет условиям (31).

Выполнение целевого условия манипулятором осуществляется в общем случае не единственным способом. Разные варианты траекторий возникают при изменении начальных параметров b_j.

2.6. Программы для планирования траекторий движения робота

Планирование движений тележки и манипулятора мобильного робота с учетом препятствий в ходе лабораторной работы проводится с помощью соответствующих программ, выполненных в среде Delphi и основанных на уравнениях, которые рассматривались в пунктах 2.32.5.

В начале программы для планирования траекторий движения транспортной тележки задаются постоянные величины для тележки (ее длина, ширина), величина  - области. Затем вводятся начальные х(t₀), y(t₀) и конечные x(t_T), y(t_T) значения координат центра масс тележки, начальные значения параметров b₁, b₂, b₃, входящие в уравнение для кубического полинома.

Далее в соответствии с параметрами препятствий рассчитываются координаты вершин прямоугольников, в которые заключены препятствия. Для воспроизведения препятствий на экране дисплея в среде Delphi достаточно задать координаты диагональных точек прямоугольников. На основе ранее заданной величины  - области рассчитываются координаты запрещенной зоны, ближе которой центр масс тележки не должен подходить к препятствию.

После определения всех необходимых параметров организуется цикл по времени. При начальном выборе направления движения тележки на заданную точку рассчитывается курсовой угол (t, b₂, b₃), обеспечивающий движение к конечной точке по кратчайшему расстоянию (по прямой), при этом b₂=b₃=0. По курсовому углу определяются координаты x(t, ), y(t, ).

Для текущего значения x(t) определяются параметры a_i, b_i, такие, что a_i<x(t) b_i; в соответствии с ними рассчитываются значения _i, _i. При этом для координаты y(t) должно выполняться неравенство |y(t)-_i|<_i. Это означает, что тележка находится в зоне, где она не задевает ни одно из препятствий.

Если данное неравенство верно, то время в цикле увеличивается на период дискретности и начинается следующий шаг цикла со старыми коэффициентами b₂, b₃. Если условие нарушается (что говорит о столкновении тележки с препятствием), то производится коррекция коэффициентов b₂, b₃ посредством рассмотренных ранее выражений для конечно-сходящегося алгоритма «Полоска - 1». Измененные параметры b₂, b₃ задаются на новом этапе расчета как начальные и цикл начинается снова (t=0). Так продолжается до тех пор, пока для всех участков при перемещении тележки не будет выполняться условие |y(t)-_i|<_i.

Расчеты завершаются после того, как координаты х(t) и y(t) попадут в окрестность заданной опорной точки: x(t)=x(t_T), y(t)=y(t_T), где  – точность позиционирования тележки. Последние значения коэффициентов b₂, b₃ принимаются как результат вычислений и коррекции и выводятся на экран.

Далее открывается графический режим. Производятся расчет и построение системы координат, а также строятся препятствия по рассчитанным ранее координатам. Построение движения тележки производится в цикле по времени. При этом используются полученные коэффициенты b₂, b₃.

Программа для планирования траекторий манипулятора мобильного робота аналогична описанной выше программе для тележки.

Сначала определяются типы переменных и массивов, вводятся начальные значения координат х(t₀) и y(t₀) схвата манипулятора и их конечные значения x(t_T), y(t_T), а также величина  - области.

Для начала расчета задаются начальные параметры b₀, b₁, b₂, b₃ полинома, входящего в уравнение (33). Из уравнения (33) следует, что в начальный момент времени коэффициент b₀ однозначно определяется равным начальному значению координаты х(t₀). Коэффициент b₁ равен начальной скорости .

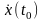Далее задаются координаты диагональных точек прямоугольников, которыми аппроксимируются препятствия. На основе ранее заданной величины -области рассчитываются координаты запрещенной зоны, ближе которой схват манипулятора не должен подходить к препятствию.

После определения всех необходимых параметров организуется цикл по времени. В нем рассчитываются текущие координаты схвата манипулятора y(t) и x(t, b₂, b₃). Маневрирование схвата осуществляется за счет нелинейного закона управления по горизонтальной координате.

Для текущего y(t) определяются параметры с_i, d_i такие, что c_i < y(t)  d_i, в соответствии с ними рассчитываются значения _i, _i. При этом для х(t) должно выполняться неравенство |х(t)-_i|<_i. Это означает, что центр схвата манипулятора находится в зоне, где он не задевает ни одно из препятствий.

Если данное неравенство верно, то время в цикле увеличивается на период дискретности и начинается следующий шаг цикла со старыми коэффициентами b₂, b₃. Если условие нарушается, что говорит о столкновении манипулятора с препятствием, то производится коррекция коэффициентов b₂, b₃ посредством выражений для КСА «Полоска - 1». Измененные параметры задаются как начальные и цикл начинается снова (t=0), до тех пор, пока для всех участков траектории движения манипулятора не будет выполняться условие |х(t) - _i|<_i.

Расчеты завершаются после того, как координаты х(t), y(t) попадут в окрестность заданной опорной точки: x(t)=x(t_T), y(t)=y(t_T), где  –точность позиционирования манипулятора.

Последние значения коэффициентов b₂, b₃ принимаются как результат вычислений и коррекции и выводятся на экран. Далее открывается графический режим. Построение ПД манипулятора производится в цикле по времени.

С помощью описанных программ можно получать различные траектории движения тележки и схвата манипулятора. Для уменьшения времени расчетов необходимо сложные траектории разбивать на более простые отрезки.