5. Вычеты и их приложения
5.1. Основная теорема о вычетах
Пусть
функция
аналитична в области
за исключением конечного числа
изолированных особых точек однозначного
характера
лежащих в области
.
Поставим задачу вычислить интеграл
по
кусочно-гладкому замкнутому контуру Г
- границе области
.
Построим окружности
,
выбрав
так, чтобы в круг
не
попала ни одна точка
.
По теореме Коши о составном контуре
(многосвязной области) можно записать
.
Функция
- аналитическая в кольце
,
следовательно, она может быть разложена
в нем в ряд Лорана, который равномерно
сходится на границе
,
так как на
ней нет
особых точек:
Вычислим
при целом
.
Если
неотрицательно, то подынтегральная
функция аналитична в круге
,
следовательно, по интегральной теореме
Коши
.
Если
,
то по следствию из интегральной формулы
Коши (формуле для производной) получим
.
При
по интегральной формуле Коши
.
Таким образом,
,
.
Вычетом
функции
относительно изолированной особой
точки
называется коэффициент
при
разложении
в ряд Лорана в окрестности точки
.
Таким образом, получена формула
.
Тем
самым доказана основная теорема о
вычетах, которая формулируется
следующим образом. Пусть
однозначна и
аналитична в области
за исключением конечного числа
изолированных особых точек. Тогда
интеграл от
,
взятый по кусочно-гладкому замкнутому
контуру, содержащемуся в
и
не проходящему через особые точки,
равен произведению суммы вычетов
относительно всех особых точек,
заключенных внутри Г , на
.
Поэтому, зная вычеты функции в особых точках, легко вычислить интеграл.
5.2. нахождение вычетов в особых точках
Рассмотрим вычисление вычетов в особых точках конечной плоскости различного типа.
Пусть - устранимая особая точка. В этом случае в разложении в ряд Лорана отсутствует главная часть, следовательно, коэффициенты при всех отрицательных степенях - нулевые, т.е. вычет равен нулю. Пусть - полюс первого порядка. Тогда разложение в ряд Лорана имеет вид
Умножая
на
и переходя к пределу при
,
получим
.
Пусть
,
где
(в этом случае - тоже полюс первого порядка функции ).
Определим вычет в точке :
.
Пусть - полюс k-го порядка функции. Тогда разложение в ряд Лорана имеет вид
Умножая
на
,
дифференцируя
раз и переходя к пределу при
получим
Если - существенно особая точка, то приходится выписывать разложение в ряд Лорана и искать .
Примеры. Классифицировать особые точки:
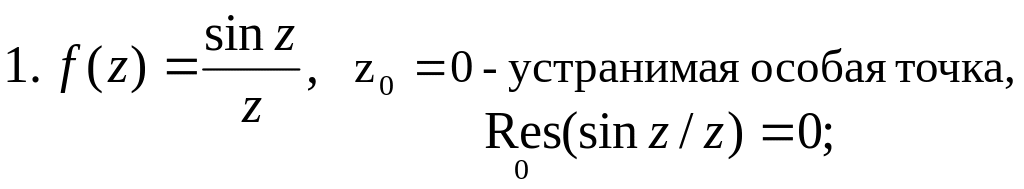
5.3. Вычисление интеграла от функции комплексной переменной
Примеры:
1.
вычислить интеграл
,
Решение:
в области Dг
, ограниченной
Г, находится
-
полюс первого порядка, полюс второго
порядка
в область не входит и не должен учитываться
при вычислении интеграла:
2. вычислить интеграл
Решение:
в области DГ , ограниченной контуром Г, функция f(z) – аналитическая, по интегральной теореме Коши искомый интеграл равен нулю;
3. вычислить интеграл
Решение:
существенно
особая точка
входит в область DГ
,
Упражнение: вычислить интегралы
1.
3.
;
4.
;
5.
.
В
ряде примеров удобно использовать вычет
в бесконечно удаленной точке
,
где
- коэффициент при первой отрицательной
степени в разложении функции в ряд
Лорана в окрестности бесконечно удаленной
точки. Найдем разложения в ряд Лорана
и вычеты в бесконечно удаленной точке
для функций:
а)
;
б)
.
Решение:
а)
.
Сделаем замену:
:
Таким
образом» бесконечно удаленная точка
для функции
является устранимой точкой, так как в
разложении отсутствуют члены с
положительными степенями. Найдем вычет:
.
б)
Сделаем замену
:
Бесконечно удаленная точка для функции является существенно особой точкой, вычет в ней равен нулю.
Справедлива теорема: сумма вычетов функции, аналитичной во всей расширенной плоскости за исключением конечного числа изолированных особых точек, по всей расширенной плоскости равна нулю.
В
самом деле, если выбрать кусочно-гладкий
контур Г
, охватывающий все особые точки конечной
плоскости
,
то, проходя его в положительном
направлении, по теореме о вычетах имеем:
.
Проходя его в отрицательном направлении (в области одна особая точка - бесконечно удалённая), получим
.
Складывая окончательно, имеем:
С помощью этой теоремы иногда легко вычислить интегралы, которые иным способом посчитать трудно.
Пример: вычислить
.
Решение:
Ясно,
что бесконечно удаленная точка - нуль
второго порядка
,
причем в лорановском разложении в ее
окрестности
нет
члена с
первой отрицательной степенью, поэтому
вычет в бесконечно удаленной точке
равен нулю и интеграл также равен нулю.
5.4. Вычисление несобственных интегралов
С помощью теоремы о вычетах можно вычислять интегралы вида
.
Теорема:
пусть
аналитична
в
за исключением
конечного числа изолированных особых
точек
.
Пусть
при
совпадает с
.
Пусть существуют константы
,
такие, что для любого
справедлива оценка
.
Тогда:
.
Пример: вычислить
.
Решение:
Рассмотрим
,
она аналитична в
,
за исключением точки
-
полюса второго порядка. Выбирая
,
имеем
.
Применяя теорему,
получим:
.
Некоторые приемы вычисления несобственных интегралов с помощью теоремы о вычетах основаны на использовании леммы Жордана и ее следствий. Лемма Жордана используется при доказательстве общей теоремы разложения в операционном исчислении.
.Лемма
Жордана: пусть
аналитична в
(
-любое
наперед заданное число), за исключением
конечного числа изолированных особых
точек, и равномерно относительно
(
)
стремится к нулю при
.
Тогда
,
где
и
-
дуга полуокружности
В
операционном исчислении используется
несколько иная формулировка леммы:
,
,
удовлетворяет условиям леммы в
(
-
фиксирование).
-дуга полуокружности
.
Следствие
из леммы Жордана: пусть
удовлетворяет условиям леммы Жордана,
пусть
не имеет особых точек на действительной
оси,
.
Тогда
.
Эту формулу можно модифицировать для четных и нечетных функций:
=
=
.
Если
-
нечетная функция, то
Если f(x) – четная функция, то
.
Пример:1) вычислить несобственный интеграл
,
Решение:
;
;
2.
вычислить несобственный интеграл
.
Решение:
;
.
Упражнение: вычислить интегралы
1)
2)
.
6. ПРИМЕНЕНИЕ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ К РЕШЕНИЮ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ИСИСТЕМ ЭТИХ УРАВНЕНИЙ
6.1. Решение задачи Коши для нулевых начальных условий
Рассмотрим применение операционного метода для нахождения решения линейного дифференциального уравнения с постоянными коэффициентами, удовлетворяющего заданным начальным условиям. Покажем, что, применяя операционный метод, эту задачу можно свести к алгебраической задаче, что значительно упрощает дело.
Пусть в пространстве оригиналов имеется линейное дифференциальное уравнение n – го порядка
(33)
и требуется найти решение y(t) этого уравнения такое, что
0
Обозначим через Y(p) изображение интересующего нас решения. Учитывая свойства преобразования Лапласа, запишем уравнение для Y(p) в виде
где
,
или
Введем обозначение
,
тогда
.
Разрешим это уравнение относительно Y(p):
Таким
образом, для нахождения искомого решения
достаточно отыскать оригинал для
изображения 1/Ψ(p).
Если найдем для него оригинал, то по
теореме свертывания сразу получим
искомое решение
данного дифференциального уравнения.
Как это следует из теоремы разложения,
отыскание оригинала для изображения
1/Ψ(p)
выполняется по формуле
,
(34)
где pk – корень многочлена Ψ(p) кратности rk. Оригинал для 1/Ψ(p) можно найти и при помощи разложения на простейшие дроби.
Следовательно, решением дифференциального уравнения при выбранных начальных условиях будет функция
(35)
Совершенно ясно,
что
можно рассматривать как единое изображение
.
Особенно это выгодно в случае, когда
Φ(р) представляет собой дробно
рациональную функцию, что дает возможность
найти оригинал для изображения
без вычисления свертки.
Пример: решить уравнение
при
Решение:
Для решения данного уравнения применим (35). Найдем левую часть изображающего уравнения
Вычислим оригинал функции
А это уже табличное изображение.
Ему соответствует оригинал
,
то есть
Свернем эту функцию с
:
Таким образом,
Пример: найти решение дифференциального уравнения
при
Решение: решим уравнение, не применяя соотношения свертывания (35). Изображающее уравнение будет иметь вид
откуда находим
Следовательно,
Иногда решение-оригинал можно сразу отыскать в таблице оригиналов и их изображений, используя, конечно, грамматические правила преобразования Лапласа.
Не всегда следует рациональную дробь-изображение сразу разлагать на простейшие дроби.
Пример: решить уравнение
при
Решение: прежде
чем записать изображающее уравнение,
напомним, как находится изображение
функции
.
Из теоремы смещения следует, что если
то
Значит
,
так как
Изображающее уравнение будет иметь вид
Тогда
Применяя опять теорему смещения уже для нахождения оригинала, получим решение данного дифференциального уравнения. Зная, что
,
найдем
6.2. Применение формулы Дюамеля
Одним из наиболее простых частных случаев уравнения (33) является уравнение вида
(36)
где в правой части стоит
единичная функция
.
Пусть начальные условия нулевые, т.е.
Тогда изображающее уравнение будет иметь вид
.
Учитывая введенные выше обозначения, получим
,
откуда
Оригинал находится по второй теореме разложения.
Таким образом, в случае единичной правой части решение-оригинал находится без привлечения операции свертывания. Но не это самое важное. Оказывается, знание решения дифференциального уравнения с единичной правой частью (единичной возмущающей силой) позволяет построить решение уравнения с той же левой частью, но зато с произвольной возмущающей функцией f(t).
Пусть требуется найти решение y(t) дифференциаль ного уравнения
удовлетворяющее нулевым начальным условиям. Обозначим решение уравнения (36), удовлетворяющее также нулевым начальным условиям, через y1(t). Запишем изображающие уравнения для уравнений (36) и(33):
Здесь
Исключая
из уравнения (37) и подставляя в уравнение
(38), найдем
Предполагая,
что оригинал для изображения
известен, определим оригинал функции
,
используя формулу Дюамеля. Действительно,
привлекая формулу Дюамеля, получим
Учитывая начальные условия, окончательно найдем
(39)
Совершенно ясно, что то же самое можно получить, используя интеграл Дюамеля в других формах. Выбор той или иной формы определяется исключительно соображениями упрощения вычислений.
Пример: решить уравнение
при
Решение: решим сначала уравнение
при тех же начальных условиях:
или
Для нахождения оригинала воспользуемся второй теоремой разложения, получим
По формуле (39) находим искомое
решение. В нашем случае
Итак,
Если воспользоваться формулой (35), то
,
т.е.
Поэтому получим
Это равенство мы используем в дальнейших
рассуждениях.
Используя интеграл Дюамеля в другой форме, можно записать
Итак, получили еще одну формулу,
выражающую наряду с (39) решение
дифференциального уравнения, отвечающее
произвольному сигналу f(t), через
решение
этого же уравнения, отвечающему входному
сигналу
:
6.3. Решение задачи Коши при ненулевых начальных условиях
Рассмотрим
теперь применение операционного метода
для нахождение решения уравнения (33)
при ненулевых начальных условиях:
В этом случае изображающее уравнение будет иметь вид
Для изображения искомого частного решения получаем соотношение (с использованием выше введенных обозначений)
(41)
Коэффициенты
Ak определяются по начальным
условиям и коэффициентам исходного
уравнения. В этом случае, так же как и
при нулевых начальных условиях, для
записи решения может быть использован
оригинал g(t) для передаточной
функции
Вспомним,
что с одной стороны
с
другой стороны
,
где y1(t) – решение уравнения
с единичной правой частью
,
удовлетворяющее нулевым начальным
условиям, т.е.
Применение теоремы о дифференцировании оригинала нам дает
.
Итак, в случае ненулевых начальных условий решение- оригинал может быть записано в виде
(42)
Совершенно ясно, что последнюю формулу применять не обязательно, если решение-оригинал можно отыскать в таблице оригиналов и изображений, используя, конечно, грамматические правила преобразования Лапласа, а также элементарные алгебраические преобразования.
Притмер: решить уравнение
при
Решение: по теореме дифференцирования оригинала имеем
Найдем изображение оригиналов, стоящих в правой части исходного уравнения:
Тогда изображающее уравнение примет вид
или
,
откуда
Для представления Y(p) в виде, удобном для использования таблицы оригиналов и изображений, достаточно заметить, что
Окончательно находим
Отсюда
Пример: решить уравнение
при
Решение: перейдем к изображающему уравнению
откуда
Известно,что
Окончательно имеем
Рассмотрим решение дифференциального уравнения (33), когда начальное значение независимого переменного отлично от нулевого.
Требуется найти решение уравнения
удовлетворяющее начальным условиям
При переходе к изображающему
уравнению возникает небольшая трудность
, заключающаяся в том, что в изображения
,…,
будут
входить, согласно теоремам, начальные
значения искомой функции и ее производной
не в точке t0 , а в точке t=0.
Чтобы обойти это затруднение, применим
следующий прием. Введем новое переменное
τ по формуле τ=t+t0, откуда
.
Вместо неизвестной функции y(t)
, будем рассматривать
Очевидно, что
откуда для всех z(t)
получаем следующие начальные
условия:
Итак,
исходную задачу свели к нахождению
решения дифференциального уравнения
Удовлетворяющего начальным условиям при нулевом значении независимого переменного τ.
Пример: решить уравнение
при
Решение: сделаем
замену независимого переменного по
формуле
Тогда
Относительно
имеем дифференциальное уравнение
или
и начальные условия
Если
Изображающее уравнение имеет вид
или
Отсюда
Для получения решения y(t)
остается в последнем соотношении (правой
части) заменить τ на t-π. Итак,
Преимущество
операционного метода перед классическим
при решении дифференциальных уравнений
в том, что при применении преобразования
Лапласа не требуется определять
постоянных, следовательно, не требуется
решения системы алгебраических уравнений,
из которых находятся произвольные
постоянные. Наиболее ярко проявляется
преимущество операционного метода
перед классическим при решении линейных
дифференциальных уравнений с постоянными
коэффициентами, когда правая часть f(t)
представляет собой кусочно - непрерывную
функцию. В этом случае, используя
единичную запаздывающую функцию
можно правую часть записать единым
аналитическим выражением и по теореме
о запаздывании оригинала найти изображение
правой части. Это изображение будет
представлять собой некоторую аналитическую
в полуплоскости функцию
Ясно, что при нахождении оригинала для
изображения, полученного решением
изображающего уравнения, придется снова
воспользоваться теоремой о запаздывании
оригинала. Ответ будет содержать
запаздывающую единичную функцию, которая
автоматически склеивает аналитические
выражения для решения на разных интервалах
изменения аргумента.
При использовании
такого подхода полезно помнить следующее:
если
при t1<t<t2,
f(t)=0 при и t<t1
и t.>t2, то функцию f(t)
можно записать в виде
.
Пример: решить уравнение
при
где
Для
составления изображающего уравнения
запишем f(t) в виде
Отсюда получим изображение правой части
или
Используя
свойства преобразования Лапласа, получим
,
Окончательно
6.4. Решение систем линейных дифференциальных уравнений
Особенно ярко преимущество операционного метода перед классическим проявляется при решении систем линейных дифференциальных уравнений с постоянными коэффициентами. Здесь не только значительно сокращается вычислительная работа, но и решения получаются в более удобной форме.
Найдем решение системы (43), удовлетворяющее начальным условиям
(43)
Выполняя преобразование Лапласа с учетом того, что
получим изображающие уравнения (изображающую систему)
Перепишем изображающую систему в виде
(44)
Изображающая
система имеет две особенности: во-первых,
какого бы порядка заданная система ни
была, изображающая система образует
систему линейных алгебраических
уравнений относительно неизвестных
во-вторых, в эту систему входят начальные
значения искомых функций, что очень
удобно для нахождения частного решения
исходной системы дифференциальных
уравнений.
Полученную
систему решим по правилу Крамера
где
;
получается
из
заменой k-го столбца столбцом из
правых частей системы (44). По найденным
изображениям находим оригиналы и
получаем решение системы, удовлетворяющее
заданным начальным условиям.
Одним из важнейших преимуществ примененного метода является то, что каждая неизвестная функция может вычисляться сама по себе, независимо от вычисления остальных неизвестных функций. А это имеет большое практическое значение. Например, в теории автоматического регулирования и в теории цепочных схем исследователя часто интересует только одна единственная функция, входящая в систему дифференциальных уравнений, остальные же неизвестные могут остаться неопределенными.
Пример: решить систему
при
Перейдем к изображающей системе с учетом
того, что
Тогда
или
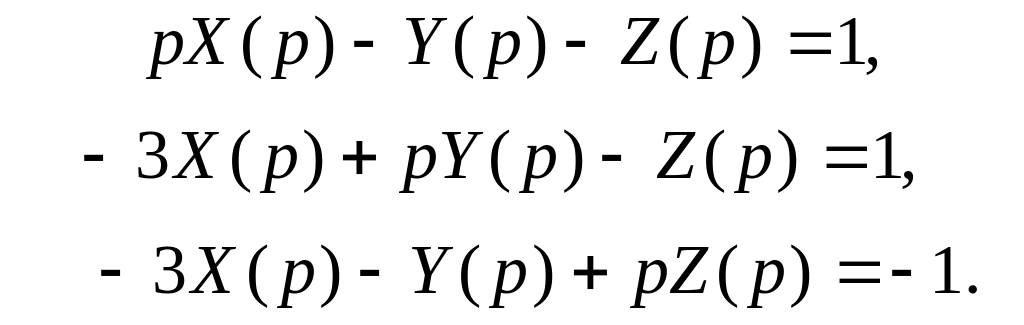
Разрешив эту систему относительно X(p), Y(p), Z(p), получим
Отсюда, применяя разложения дробей на простейшие или теоремы разложения, находим
