М.И. Зайцева В.Н. Макаров

ЭЛЕМЕНТЫ ТЕОРИИ ФУНКЦИЙ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ

Учебное пособие

Воронеж 2002

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Воронежский государственный технический университет

М.И. Зайцева В.Н. Макаров

ЭЛЕМЕНТЫ ТЕОРИИ ФУНКЦИЙ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ

Учебное пособие

Воронеж 2002

УДК 517.2

Зайцева М.И., Макаров В.Н. Элементы теории функций комплексной переменной: Учеб. пособие. Воронеж: Воронеж. гос. техн. ун-т, 2002. 84 с.

Данное учебное пособие написано в соответствии с образовательным стандартом и рабочей программой по разделу “Теория функций комплексной переменной”, изучаемому студентами специальности 130100 “Самолето-и вертолетостроение” по дисциплине “Высшая математика”. В пособии рассмотрены вопросы, связанные с дифференцированием и интегрированием функций на комплексной плоскости.

Предназначено для студентов второго курса дневного отделения.

Учебное пособие подготовлено на магнитном носителе в текстовом редакторе MS WORD 97.0 и содержится в файле “CN-1”.

Ил. 11. Библиогр.: 8 назв.

Научный редактор д-р физ. - мат. наук В.Д. Репников

Рецензенты: кафедра математики и физики Воронежского военного института радиоэлектроники;

д-р физ. - мат. наук В.А. Родин

Издается по решению редакционно-издательского совета Воронежского государственного технического университета

© Зайцева М.И., Макаров В.Н., 2002

©Оформление. Воронежский государственный технический университет, 2002

Введение

Учебное пособие предназначено для студентов высших учебных заведений, обучающихся по направлению 652100 “Авиастроение” и соответствует образовательному стандарту и рабочей программе по специальности “Самолето-и вертолетостроение”. Для этой специальности теория функций комплексной переменной используется при изучении специальных курсов таких как “Гидродинамика”, ”Газовая динамика” и некоторых других.

Вместе с тем указанный раздел математического анализа вызывает определенные трудности при изучении студентами инженерных специальностей. Учебников по теории функций комплексной переменной для высших технических учебных заведений издано сравнительно мало и изданы они давно.

Пособие содержит следующие разделы: дифференцирование и интегрирование функции комплексной переменной, элементарные функции, разложение в ряды Тейлора и Лорана, вычеты и их приложения. Для его чтения достаточно знаний лишь общего курса математики в объеме программы технических вузов. При написании авторы стремились к простоте и наглядности изложения при сохранении определенной математической строгости. Приводится подробное решение для довольно большого числа примеров. В конце каждого раздела содержатся упражнения для самостоятельного решения. Это позволяет использовать данное пособие для самостоятельной работы студентов.

1. Комплексные числа и операции над ними

1.1. Три формы записи комплексного числа

К

y

омплексным числом z называют пару чисел: x – действительная часть (Rez), y –мнимая часть (Imz). Записывают комплексное число в алгебраической форме так:

z

z

y

= x + iy,

ρ

где i – мнимая единица (i² = -1).

К

x

x

φ

омплексное число можно изобразить точкой на комплексной плоскости или радиус - вектором этой точки .

Величина называется модулем комплексного числа, угол Argz между положительным направлением действительной оси ОХ и вектором называется аргументом комплексного числа z. Argz определён при с точностью до слагаемого, кратного . Главным значением аргумента называется значение в .

,где - любое целое число.

Заметим, что

;

Тригонометрическая форма записи комплексного числа имеет вид

.

Используя формулу Эйлера

, (1)

можно записать комплексное число в показательной форме

Пример: записать комплексные числа в трёх формах.

Решение: ,

, ,

,

.

Числа называется комплексно сопряженными,

, если только - не действительное отрицательное число, для действительного отрицательного z

.

Упражнение: записать в трёх формах:

1) , 2) , 3) ;

4) , 5) , 6) , 7) .

2. Операции над комплексными числами.

Комплексные числа равны, если , . Операции сложения и вычитания комплексных чисел задаются равенством:

.

На комплексной плоскости эти операции соответствуют сложению или вычитанию радиус – векторов .

Примеры:

1) , , .

2) , .

Умножение двух комплексных чисел задается равенством:

.

Заметим, что:

Поэтому .

Деление комплексных чисел задаётся равенством :

.

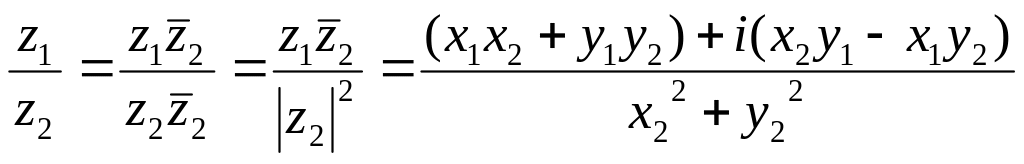Примеры:

.

Умножим два комплексных числа в тригонометрической форме:

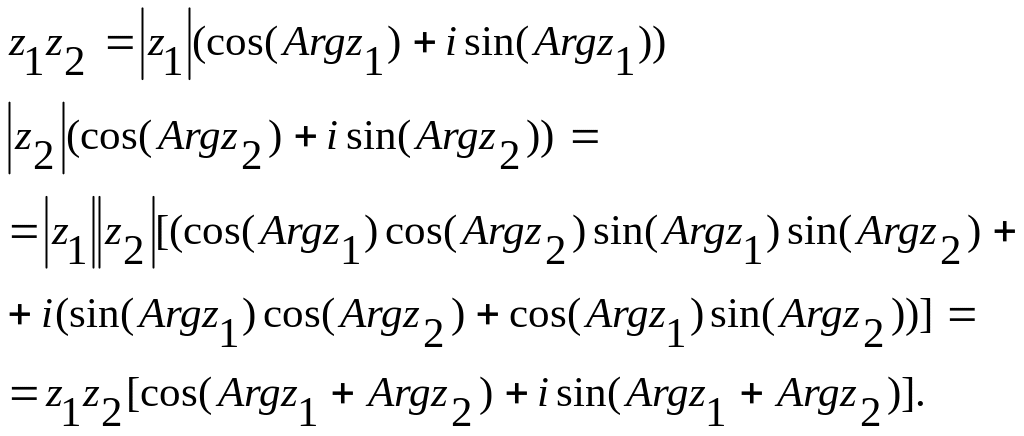
Таким образом,

Последнее соотношение понимается в том смысле, что множество значений совпадает с множеством значений Можно считать, что при умножении на вектор растягивается в раз и поворачивается на угол . Очевидно, что при делении

, .

Упражнение: вычислить

1) ; 2) .

Из правила умножения комплексных чисел в тригонометрической форме следует, что

.

С другой стороны,

.

Отсюда следует формула Муавра

.

Число называется корнем -ой степени из комплексного числа, если . В тригонометрической форме

отсюда

, .

Формула

,

или

дает n корней при . Если использовать показательную форму записи комплексного числа, эти формулы можно записать короче:

.

Легко проверить, что для любого действительного числа :

.

Поэтому все корни лежат на окружности (с центром в начале координат) комплексной плоскости и с радиусом, равным в вершинах правильного - угольника (угол между направлениями на два соседних корня равен ). Направление на первый корень составляет с положительным направлением действительной оси угол .

Пример: найти корни .

Решение: , , ,

,

,

,

.

В

y

W₄

W₃

W₂

W₁

x

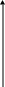
се корни расположены в вершинах квадрата на комплексной плоскости (рис 2).

Рис. 2.

Упражнения: найти корни и изобразить их на комплексной плоскости:

1) , 2) , 3) , 4) .

2. Дифференцирование функций комплексной переменной

2.1. Условие дифференцируемости функции комплексной переменной

Пусть определена и однозначна в некоторой области окрестности точки .

Функция дифференцируема в точке , если существует предел отношения полного приращения функции в точке к приращению переменного при :

.

При условии существования предел этот называется производной функции в точке и обозначается .

В лекционном курсе была доказана теорема: для того, чтобы функция , определенная в неко-торой области D, была дифференцируема в точке как функция комплексной переменной, необходимо и достаточно, чтобы функции и были дифференцируемы в той же точке (как функции двух действительных переменных) и чтобы выполнялись условия:

, . (2)

При выполнении всех условий теоремы производная может быть представлена в одной из следующих форм:

.

Условия (2) были получены Даламбером (1752г.) и Эйлером (1755г.) в связи с рассмотрением задач гидродинамики; в 1777г. Эйлер вновь получает эти условия в связи с рассмотрением интегралов от ФКП. В литературе эти условия часто называют условиями Коши-Римана,

хотя исторической справедливости ради их следовало бы называть условиями Даламбера-Эйлера.

Функция , дифференцируемая в каждой точке некоторой области D, называется аналитической (регулярной или моногенной) в этой области. Подчеркнем, что определение аналитической функции предполагает её однозначность в области D, ибо понятия предела и производной определены лишь для однозначных функций.

Во многих случаях важно иметь условия дифференцируемости функции

,

выражаемые с помощью полярных координат и . Условия эти (необхо-димые и достаточные) таковы:

1) и являются дифференцируемыми функциями и ;

2) их частные производные связаны соотношениями

, .

Для аналитических функций имеют силу обычные правила дифференцирования:

; , ; , .

Если и - взаимнообратные аналитические функции, то .