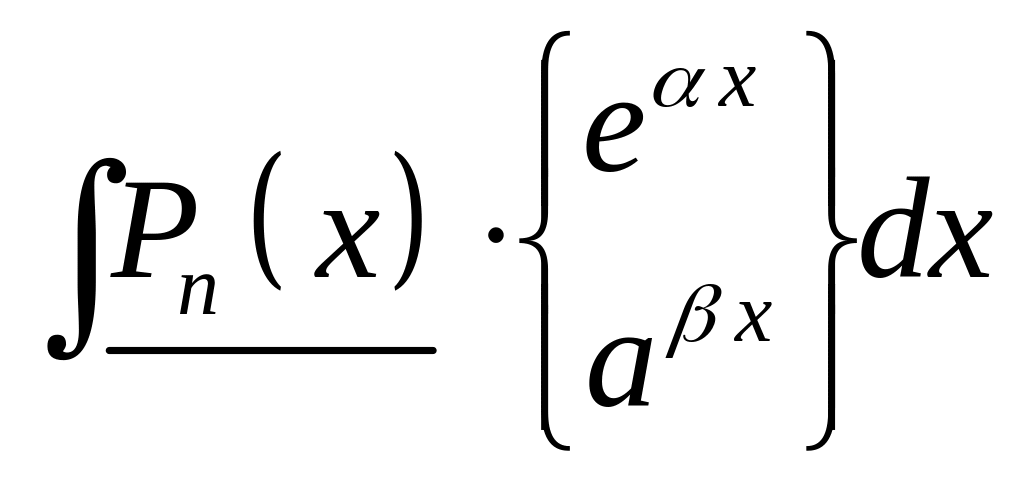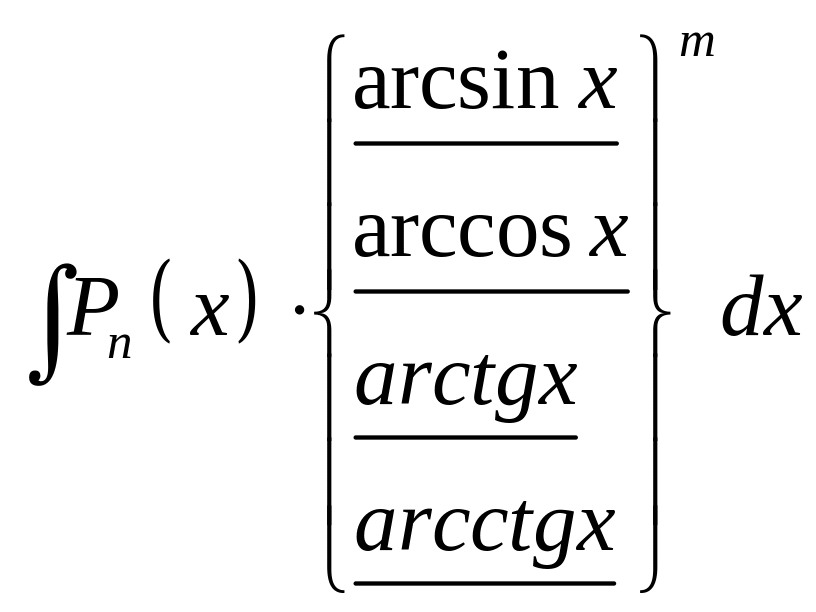- •I. Неопределенный интеграл
- •1. Таблица основных неопределённых интегралов
- •2. Основные свойства неопределённого интеграла
- •3. Замена переменной в неопределенном интеграле
- •Решение.
- •4. Интегрирование по частям
- •5. Интегрирование рациональных дробей
- •6. Интегрирование иррациональных выражений
- •7. Интегрирование тригонометрических функций
- •II. Определенный интеграл
- •1. Формула Ньютона-Лейбница
- •III. Несобственные интегралы
- •1. Несобственный интеграл I рода.
- •2. Несобственный интеграл II рода.
- •IV. Геометрические приложения определенного интеграла
- •1. Вычисление площадей плоских фигур
- •2. Вычисление длины дуги
- •3. Вычисление объёмов тел
- •Задание 1.
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •Задание 6.
- •Задание 7.
- •Задание 8.
- •Задание 9.
- •Задание 10
- •Задание 11.
- •Задание 12.
- •Задание 13.
- •Задание 14.
- •Задание 15.
- •Задание 16.
- •Задание 17.
- •Задание 18.
- •394026 Воронеж, Московский просп., 14
ФГБОУ ВПО «Воронежский государственный
технический университет»
Кафедра высшей математики
и физико-математического моделирования
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
для организации самостоятельной работы
по изучению раздела «Интегралы»
курса «Математический анализ»
для студентов направления подготовки бакалавров 080100 «Экономика»
очной формы обучения
Воронеж 2013
Составители: канд. физ.-мат. наук Е.Г. Глушко,
канд. физ.-мат. наук Е.И. Максимова
УДК 517.9
Методические указания для организации самостоятельной работы по изучению раздела «Интегралы» курса «Математический анализ» для студентов направления подготовки бакалавров 080100 «Экономика» очной формы обучения / ФГБОУ ВПО «Воронежский государственный технический университет»; сост. Е.Г. Глушко, Е.И. Максимова. Воронеж, 2013. 66 с.
В методических указаниях содержатся основные теоретические положения по интегральному исчислению функции одной переменной, изложение теоретического материала иллюстрируется большим количеством примеров и задач, приводятся задачи и упражнения для самостоятельной работы.
Методические указания предназначены для организации самостоятельного изучения студентами первого курса раздела «Интегралы» по курсу математического анализа.
Методические указания подготовлены на магнитном носителе в текстовом редакторе MS Word 2007 и содержатся в файле «INT. doc».
Ил. 7. Библиогр.: 5 назв.
Рецензент канд. физ.-мат. наук, доц. М.В. Юрьева
Ответственный за выпуск зав. кафедрой
д-р физ.-мат. наук, проф. И.Л. Батаронов
Издается по решению редакционно-издательского совета
Воронежского государственного технического университета
ФГБОУ ВПО «Воронежский государственный
технический университет», 2013
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
I. Неопределенный интеграл
Функция
F(x)
называется
первообразной
функции f(x),
заданной на
некотором множестве Х,
если
![]() для всех х
для всех х![]() Х.
Х.
Совокупность всех первообразных данной функции называется ее неопределенным интегралом:
![]() ,
,
где С – произвольная постоянная.
Для отыскания неопределенного интеграла используют таблицы основных интегралов, свойства интеграла (в частности, линейность), тождественные преобразования (так называемое непосредственное интегрирование), а также применяют различные специальные приемы, позволяющие привести исходные интегралы к табличным.
1. Таблица основных неопределённых интегралов
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
2. Основные свойства неопределённого интеграла
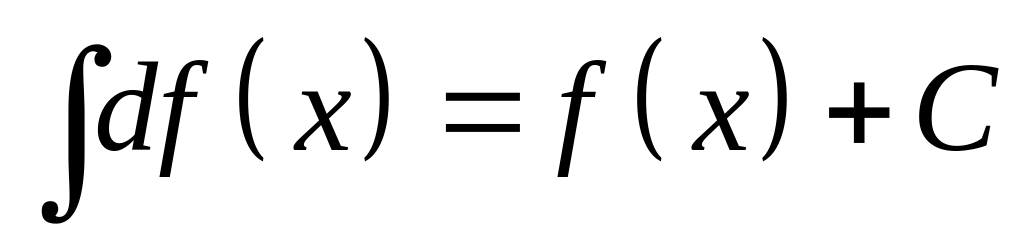 ;
;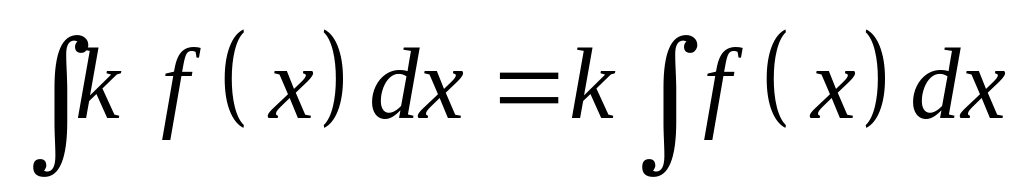 ,
где k – постоянная
величина;
,
где k – постоянная
величина;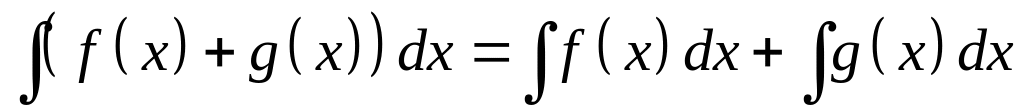 .
.
(свойства 2 и 3 составляют так называемое свойство линейности).
Пример
1. Найти
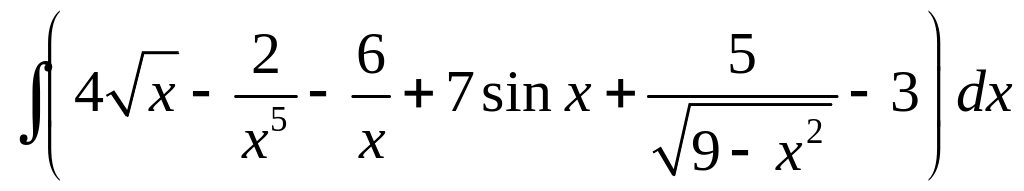 .
.
Решение.
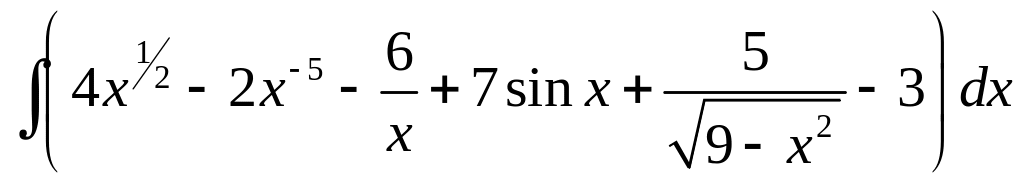 =
=
![]()
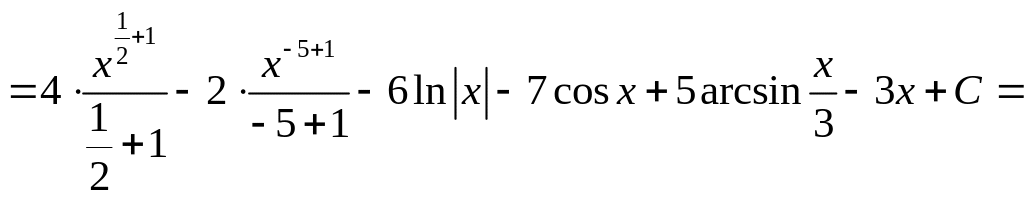
![]() .
.
3. Замена переменной в неопределенном интеграле
Формула замены переменной:
![]() ,
,
где х = φ(t), причем должна существовать обратная функция t = φ-1(x).
Пример
2.
![]() .
.
Решение. Применим подстановки: t = x², dt = 2xdx и воспользуемся формулой замены переменной:
![]() Пример 3.
Пример 3.
![]() .
.
Решение.
Сделаем замену переменной: x²
= t.
Тогда
![]() .
Следовательно,
.
Следовательно,
![]()
Пример 4. Найти интегралы:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
Решение.
а)![]()
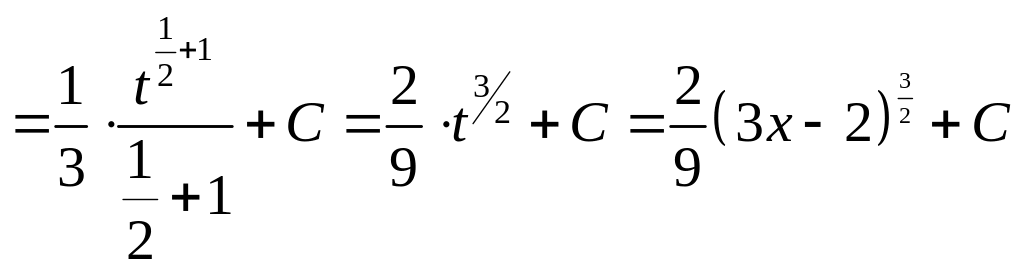 ;
;
б)
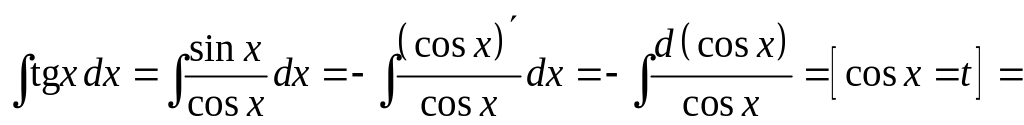
![]() ;
;
в)
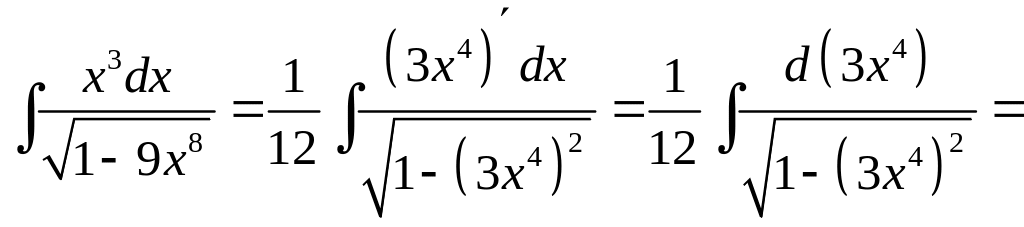
![]() .
.
Пример
5. Найти
![]() .
.
Решение.
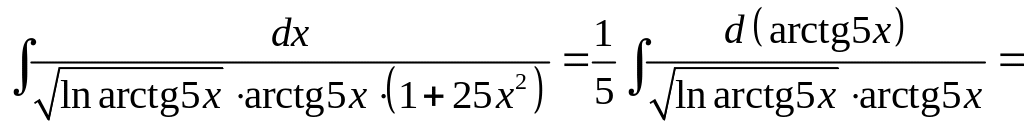
![]()
 Пример 6. Найти
Пример 6. Найти
![]() .
.
Решение.
Положим
![]() .
Тогда
.
Тогда![]() и
и
![]() Пример 7. Найти
Пример 7. Найти
![]() .
Решение. Применим подстановку
.
Решение. Применим подстановку
![]() .
Тогда
.
Тогда
![]() .
Имеем
.
Имеем

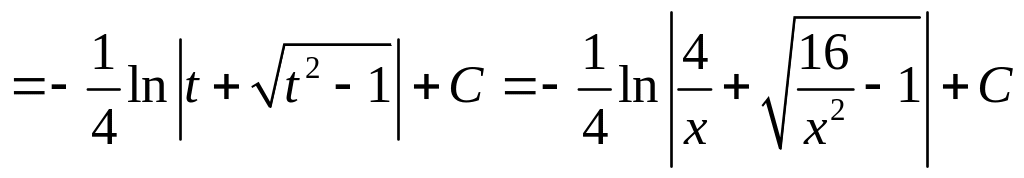 .
.
4. Интегрирование по частям
Формулу интегрирования по частям:
![]()
полезно применять в случае, когда подынтегральное выражение представляет собой произведение двух функций, одна из которых является многочленом, или если подынтегральная функция не имеет табличной первообразной (логарифм, обратные тригонометрические функции и т.п.).
Эту формулу следует применять, также, в тех случаях, когда подынтегральное выражение vdu проще исходного выражения udv.
Кроме того, интегрирование по частям применяется для получения уравнений, из которых можно найти искомую первообразную. Такие возможности возникают, когда подынтегральное выражение содержит произведение множителей вида sin kx или cos kx и enx, и в некоторых других случаях.
Ниже приведены основные типы интегралов, берущихся по частям.
I тип |
II тип |
III тип (интегралы, приводящиеся к себе) |
|
|
|
За
u принимаются
подчёркнутые функции, за dv
– остальная часть подынтегрального
выражения. Pn
(x) – многочлен степени
n. Интегралы I
типа берутся путём интегрирования по
частям n раз, II
типа – m раз, III
типа (за исключением двух последних) –
2 раза (причём, в первом интеграле III
типа оба раза за u
можно принять как
![]() ,
так и тригонометрические функции
,
так и тригонометрические функции
![]() ,
,
![]() ).
).
По частям могут быть взяты и интегралы, не вошедшие в эту таблицу.
Пример 8. Найти интегралы:
а)![]() ;
б)
;
б)![]() ; в)
; в)
![]() .
.
Решение.
а)
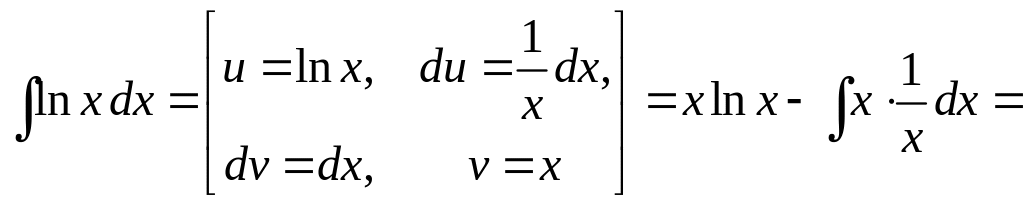
![]() .
.
Здесь и ниже при нахождении v при известном dv мы полагаем С = 0 (как в этом случае: dv = dx, отсюда следует v = x + C, но мы берём одну из первообразных v = x ).
б)
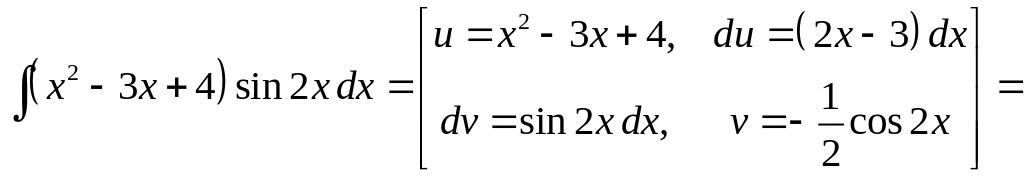
![]()
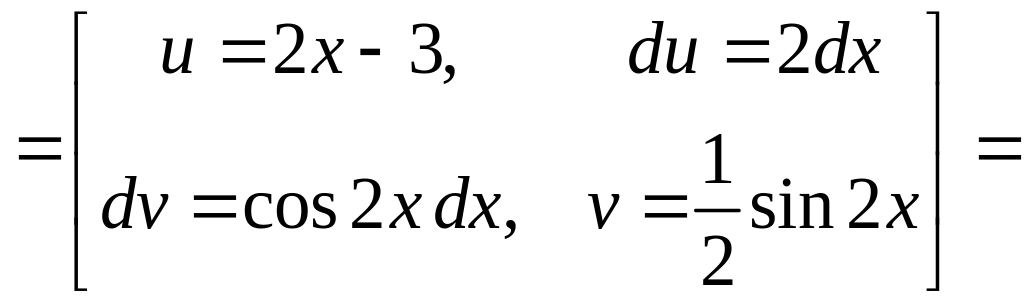 …………
…………
![]()
![]()
![]() .
.
в)
Обозначим
![]() .
Имеем
.
Имеем
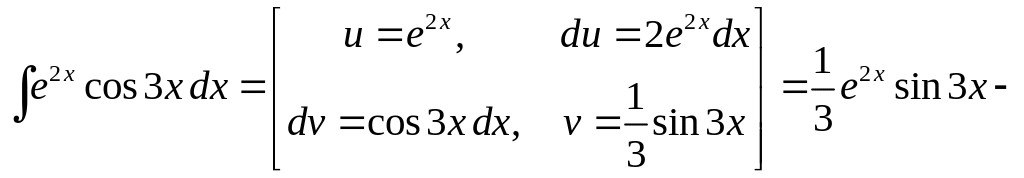

![]()
![]() .
.
Получается,
что
![]()
Отсюда находим (учитывая, что J является семейством функций, отличающихся друг от друга на постоянную величину)
![]() .
.