3. Обратная матрица. Решение систем линейных уравнений матричным способом

Матрица называется обратной к квадратной матрице , если , где – единичная матрица. Для невырожденной квадратной матрицы (6), существует единственная обратная матрица

, (11)

где - есть алгебраические дополнения элементов матрицы . Отметим, что если - вырождена ( ), то обратной к ней не существует.

Пример 7. Найти матрицу , обратную к матрице .

Решение. Вычисляем , значит - не вырождена и существует. Найдем алгебраические дополнения элементов матрицы :

; ; , и т.д. , , , , , .

Следовательно, .

Кроме методов Крамера и Гаусса решения систем линейных алгебраических уравнений для квадратных систем вида

(12)

существует матричный способ решения, согласно которому систему удобно представить в виде произведения матриц , т.е . Из последнего уравнения, умножением на обратную матрицу обеих частей равенства , получим , т.е.

(13)

Пример 8. Найти общее решение системы .

Решение. 1. Основная матрица системы имеет вид

, ее обратная вычислена в примере 7.

2. Найдем общее решение по формуле (13) .

Ответ: , , .

Замечание. Матричный способ удобно применять в тех случаях, когда нужно решать одну и туже не вырожденную систему с разными правыми частями. Определив один раз обратную матрицу для матрицы , можно легко находить соответствующие решения системы.

4. Ранг матрицы. Решение систем линейных уравнений

Выделим в произвольной матрице (1) k произвольных столбцов и k произвольных строк, где . Определитель k-ого порядка, составленный из элементов матрицы , расположенных на пересечении выделенных строк и столбцов, называется минором k-ого порядка матрицы .

Рангом матрицы называется наибольший порядок минора, определитель которого отличен от нуля (таких определителей может быть несколько).

Базисным минором является всякий отличный от нуля ее минор, порядок которого равен рангу данной матрицы.

На практике для вычисления ранга матрицы удобно приводить ее к трапециевидной форме

(14)

с помощью элементарных преобразований, не изменяющих ранга матрицы, к которым относятся:

1. умножение произвольного ряда матрицы на число, отличное от нуля;

2. прибавление к одной строке (столбцу) матрицы другой строки (столбца), умноженной на произвольное число;

3. перестановка местами двух параллельных строк (столбцов) матрицы;

4. вычеркивание из матрицы одной из одинаковых (или пропорциональных) строк (столбцов);

5. вычеркивание нулевой строки (столбца).

Пример 9. Найти ранг матрицы и указать базисный минор.

Решение. Выполняя последовательно перечисленные ниже элементарные преобразования, получим

.

1. – весь последний столбец умножен на ;

2. – ко второй строке прибавлена первая; к третьей строке прибавлена первая, умноженная на (–2); к четвертой строке прибавлена первая, умноженная на (–3);

3. – отброшена одна из равных строк;

4. – к третьей строке прибавлена вторая, умноженная на 3.

Последняя матрица имеет трапециевидную форму и ранг ее равен 3 – количество ненулевых строк. Следовательно, ранг исходной матрицы также равен 3.

Рангообразующий минор находится в первых 3-х строках и столбцах, т.е.

. Ответ: , минор является базисным.

Пусть дана система m уравнений с n неизвестными

, (15)

Напомним, что система называется совместной, если у нее существует, по крайней мере, одно решение, в противном случае она называется несовместной.

Теорема Кронекера-Капелли. Для того чтобы система (15) была совместной, необходимо и достаточно, чтобы

, (16)

где - основная матрица, составленная из коэффициентов перед неизвестными, а = – расширенная матрица системы.

При решении системы (15) возможны два случая:

1) если , то система несовместна,

2) , то система совместна, причем при система имеет единственное решение (которое может быть определено методами Крамера, Гаусса и обратной матрицы), а при система имеет бесчисленное множество решений и решить такую систему возможно только методом Гаусса.

Отметим, что определение совместности системы рекомендуется начинать с вычисления ранга расширенной матрицы , при вычислении которого нельзя переставлять последний столбец. Ранг основной матрицы определяется по рангу полученной из матрицы, у которой отбросили последний столбец.

Если система совместна и имеет бесконечное множество решений , то без ущерба общности можно считать, что базисный минор располагается в первых строчках и столбцах расширенной матрицы , тогда отбросив последние уравнений системы (15), записываем укороченную систему:

, (17)

которая эквивалентна исходной.

Неизвестные называются базисными, а – свободными. Перенося слагаемые, содержащие свободные неизвестные, в правую часть уравнений (17), получим систему относительно базисных неизвестных:

,

которая для каждого набора значений свободных переменных имеет единственное решение ,…, . Итак, общее решение системы (15) содержит произвольных постоянных и имеет вид

, (18)

Пример 10. Установить совместность системы линейных уравнений

Решение. Выпишем расширенную матрицу = .

и вычислим её ранг:

= . Так как = , то . Очевидно , так как при отбрасывании последнего столбца третья строка будет нулевой. В силу теоремы Кронекера-Капелли система несовместна.

Пример 11. Найти общее решение системы линейных уравнений

Решение. Выпишем матрицу и вычислим её ранг.

= ~ ~ .

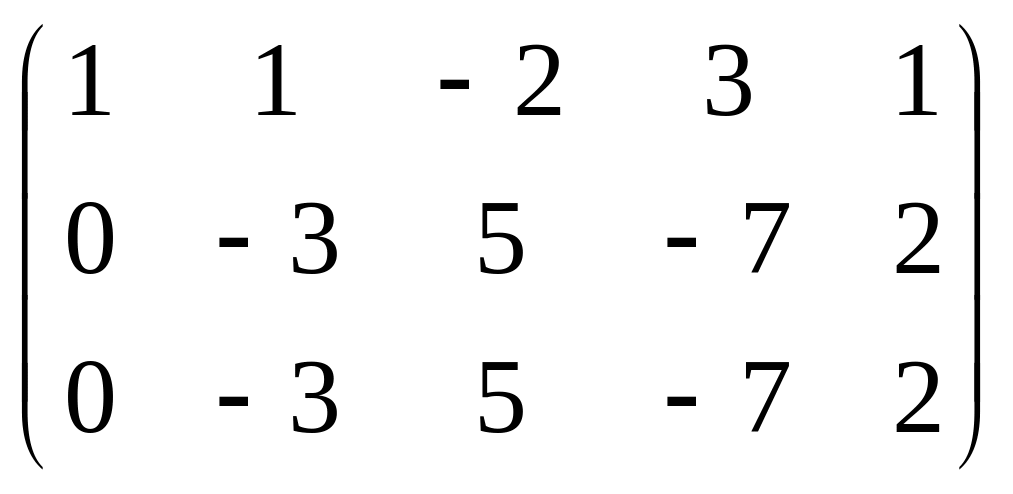Следовательно, , а значит система совместна.

Поскольку , то система имеет бесчисленное множество решений, выпишем из последней матрицы эквивалентную исходной систему

.

Выберем переменные и в качестве свободных и перенесем их вправо:

.

Найдем из второго уравнения системы , тогда из первого .

Соответствующее общее решение исходной системы имеет вид

,

где , . Укажем хотя бы одно решение из всего множества решений. Например, при получаем решение .

Важным частным случаем линейных систем являются однородные

, (19)

где . Она всегда совместна, так как основная матрица системы отличается от расширенной одним последним нулевым столбцом, который не изменяет на ранг матрицы, т.е. и, значит, всегда имеет решение, по крайней мере – тривиальное решение .

Для существования нетривиальных решений произвольной однородной системы (19) необходимо и достаточно, чтобы .

Для существования нетривиального решения квадратной однородной системы (19) необходимо и достаточно, чтобы , что тоже следует из условия .

Решением системы является упорядоченный набор чисел, который обращает в тождество каждое уравнение системы, или просто вектор. Далее введем некоторые понятия векторной алгебры, которые легко описывают структуру решения системы.

Если записать однородную систему (19) в матричной форме (решениями которой являются векторы размерности ), то в силу линейных свойств матрицы сумма решений и решение, умноженное на константу, тоже будет решением этой системы. Так как среди всех решений есть тривиальное, то множество всех решений системы (19) будет подпространством размерности

(20)

Полагая по очереди в формуле (18) одно из свободных неизвестных (например, равное единице), а все остальные равные нулю, можно выбрать базис в этом пространстве (его еще называют фундаментальной системой решений) и найти общее решение системы (19) по формуле

, (21)

где .

Пример 12. Найти фундаментальную систему решений и общее решение системы

Решение. Выпишем матрицу и вычислим ранг этой матрицы.

= ~ ~ .

Очевидно, , а значит система совместна. Поскольку , то базис множества решений системы состоит из двух векторов, так как по формуле (20) .

Вычисление ранга расширенной матрицы по преобразованиям совпадает с решением системы методом Гаусса, тогда отбросив последнюю нулевую строку, получим эквивалентную систему

Выбрав неизвестные , в качестве свободных, выразим базисные переменные , через свободные:

.

1. полагая , , тогда система имеет вид , откуда и , что дает первый базисный вектор ;

2) полагая , , тогда система имеет вид , откуда и , что дает второй базисный вектор .

По фундаментальной системе решений найдем общее решение системы по формуле (21)

.

Замечание. В случае бесчисленного множества решений есть важная связь между решением неоднородной системы и соответствующей ей однородной системы. Если какое-либо частное решение системы (15), а общее решение системы (19), то общее решение неоднородной системы (15) определяется формулой

. (22)

Пример 13. Найти общее решение системы .

Решение. Заметив, что третье уравнение системы является суммой первых двух уравнений и есть минор , можно сделать вывод, что и у данной системы будет бесчисленное множество решений. Рассматриваемой системе соответствует однородная система, которая решена в предыдущем примере 12: .

Далее определим какое-либо неоднородное решение системы, опираясь на факт, что базисными переменными будут и , а свободными и . Зададим свободным переменным значения и , тогда система примет вид

, тогда .

Итак, общее решение имеет вид

, .