Задача №5

Решить систему линейных уравнений двумя способами

1. методом Крамера;

2. используя обратную матрицу.

Решение. 1) Решим систему уравнений методом Крамера. Решение системы трех линейных уравнений с тремя неизвестными

находится по формулам

,

где

(предполагается, что Δ ≠ 0),

, , .

Для данной системы уравнений имеем

Вспомогательные определители

, ,

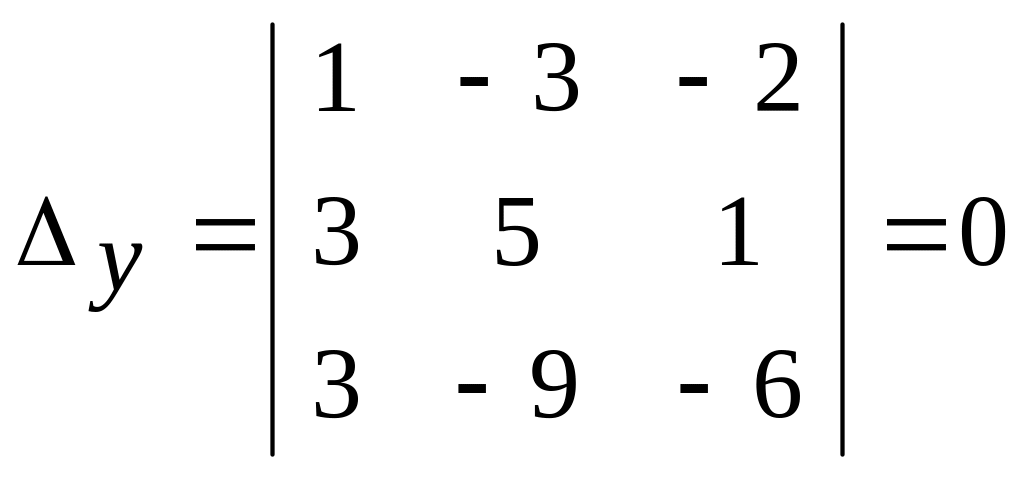Решение системы уравнений

.

2) Решим теперь систему матричным методом. Запишем исходную систему уравнений в матричном виде

,

где

Решение матричного уравнения имеет вид

,

где – матрица, обратная к матрице А. Заметим, что поскольку определитель матрицы А не равен нулю ( , см. п. 1), то матрица системы невырожденная и, следовательно, имеет обратную.

Обратная матрица находится по формуле

,

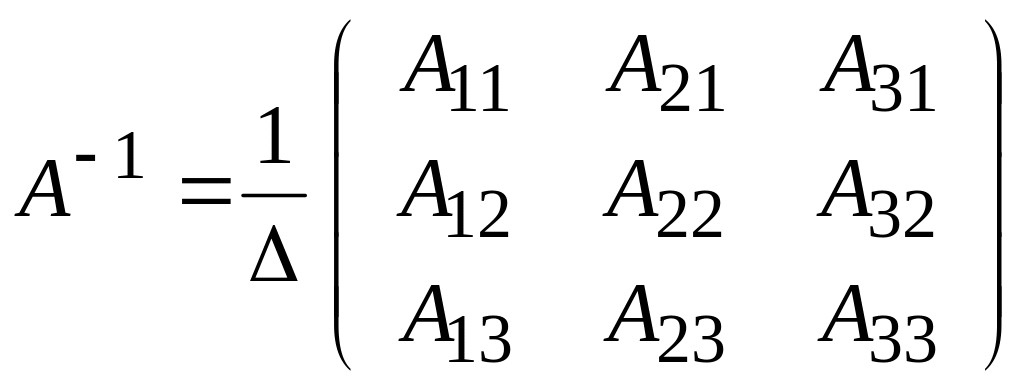где Δ – определитель матрицы А, – алгебраическое дополнение элемента определителя матрицы А. Вычислим алгебраические дополнения:

Таким образом,

,

откуда

Следовательно, , , .

Задача №6

Решить систему линейных уравнений методом Гаусса.

Решение. Метод Гаусса основан на приведении системы уравнений к треугольному виду. Это достигается последовательным исключением неизвестных из уравнений системы.

Разделим первое (разрешающее) уравнение на 3. Затем, последовательно умножая его на -2, -4, -5, прибавим его ко второму, третьему и четвертому уравнениям исходной системы. В результате получим систему, в которой неизвестное исключено из второго, третьего и четвертого уравнений

Теперь второе уравнение будет разрешающим с разрешающим коэффициентом . Разделим второе уравнение на и прибавим преобразованное второе уравнение, умноженное последовательно на и , к третьему и четвертому уравнениям системы. В результате получим систему, в которой неизвестное исключено из третьего и четвертого уравнений

или

Разделим третье уравнение на и прибавим преобразованное третье уравнение, умноженное на , к четвертому уравнению системы. В результате получим систему, в которой неизвестное исключено из четвертого уравнения

или

Приведение исходной системы уравнений к треугольному виду называется прямым ходом метода Гаусса. Далее реализуем обратный ход метода Гаусса.

Подставляя значение в третье уравнение, найдем

Найденные значения и подставим во второе уравнение и определим

Зная , и , из первого уравнения определим

Таким образом, , , , .

Задача №7

Перед решением задачи 7, советуем изучить следующий материал.

Общим уравнением кривой второго порядка называется уравнение вида

, (1)

где коэффициенты и - любые числа и, кроме того, числа и не равны нулю одновременно.

Попытаемся упростить это уравнение путем перехода к другим координатам. В результате преобразования нужно добиться:

1) Чтобы в группе старших членов исчез член с произведением текущих координат.

2) Чтобы число членов первой степени стало наименьшим, а если возможно – совсем их уничтожить.

3) Если возможно уничтожить свободный член.

В результате мы получим уравнение кривой второго порядка, называемое каноническим.

а) Прежде всего попытаемся упростить уравнение (1) путем параллельного переноса координатных осей. Перенесем начало координат в точку , которую пока будем считать произвольной. Из формул преобразования при параллельном переносе следует

, (2)

где и - новые координаты произвольной точки. Подставляя (2) в (1), получим

где .

В преобразованном уравнении (3) члены первой степени исчезнут, если и подобрать так, чтобы удовлетворялись уравнения

. (4)

Обозначим буквой определитель системы (4)

.

Этот определитель составлен из коэффициентов при старших членах уравнения (1) и называется дискриминантом старших членов этого уравнения. Если , то система (4) совместна и имеет единственное решение . С учетом (4) уравнение (3) примет вид

(5)

где свободный член с учетом (4) можно преобразовать

или

. (6)

Вернемся к уравнению (5). При замене на его левая часть не меняется. Это значит, что если точка лежит на кривой, определяемой уравнением (5), то и симметричная ей точка также лежит на этой кривой. Но точки и симметричны относительно точки . Поэтому точка в этом случае называется центром симметрии или просто центром данной кривой. Теперь становится очевидным геометрический смысл преобразования, при котором исчезают члены первой степени: начало координат переносится в центр кривой.

Определение. Кривая второго порядка, имеющая единственный центр, называется центральной. Признаком центральной кривой служит неравенство .

б) Продолжим упрощение уравнения (5). Попытаемся уничтожить член, содержащий произведение путем поворота перенесенных осей на некоторый угол . Из формул преобразования координат при повороте осей следует

, (7)

.

Подставляя (7) в уравнение (5) и приводя подобные, получим

В уравнении (8) члены с произведением исчезнут, если угол поворота выбрать так, чтобы коэффициент при обратился в нуль

,

или

.

После деления на , получим

. (9)

Уравнение (9) является квадратным уравнением относительно . Решив его, в общем случае мы найдем два корня: и . Однако в формулах для поворота (7) фигурируют и . Зная , их легко найти по формулам тригонометрии

. (10)

Знак выбирается в зависимости от того, в какой четверти находится угол, определяемый соответствующим .

В системе координат, повернутой на угол , опреляемый по (10), уравнение (8) примет вид

, (11)

где и - постоянные коэффициенты при и в уравнении (8). Уравнение (11) представляет собой канонический вид общего уравнения центральной линии второго порядка.

Пример 1. Привести к каноническому виду уравнение

. (а)

Решение. Здесь . Прежде чем использовать изложенную схему, нужно убедиться, что данное уравнение представляет центральную линию второго порядка. Составим определитель . Следовательно, данная линия центральная и для освобождения в ее уравнении от членов первого порядка перенесем начало координат в центр этой линии. Его координаты удовлетворяют уравнениям

Центр линии располагается в точке . Подсчитаем, чему будет равен свободный член после переноса начала координат в т. : . Само уравнение после применения параллельного сдвига , примет вид

. (б)

Для освобождения от члена, содержащего произведение , применим преобразование поворота осей на некоторый угол

,

.

Для определения конкретного значения угла имеем уравнение

или .

Отсюда и . Выберем положительное значение , что соответствует острому углу поворота осей . Тогда . Формулы поворота в этом случае имеют вид

,

. (в)

Подставляя (в) в (б), получим

.

Раскрывая скобки и приводя подобные, имеем

,

, .

Делим на (-16), тогда .

Получено каноническое уравнение гиперболы с действительной полуосью , мнимой . Выполним последовательное построение этой гиперболы (рис. 6).

Рис. 6

Замечание. Из сопоставления с классификацией линий второго порядка получаем, что уравнение центральной линии может быть только эллиптического или гиперболического типа .

Для уравнения параболического типа . Схема приведения к каноническому виду уравнения центральной линии здесь не годится. Упрощение параболического уравнения целесообразно начать с поворота координатных осей на угол при помощи формул

,

.

Угол поворота определится из уравнения

.

В преобразованном уравнении исчезнет член с произведением . Дальнейшее упрощение преобразованных уравнений достигается путем параллельного переноса уже повернутых осей.

Пример 2. Привести к каноническому виду уравнение

. (а)

Решение. Здесь . Вычислим . Данная линия принадлежит к параболическому типу. Для освобождения от члена, содержащего произведение координат, повернем оси на угол , определяемый из уравнения . В нашем случае или . Его решения и . Возьмем первое значение . В этом случае .

Преобразование координат будет иметь вид

,

. (б)

Подставляя (б) в (а), получим

, или .

Данное уравнение не содержит члена с произведением . Дальнейшее упрощение производится с помощью параллельного переноса координатных осей. Для этого выделим полный квадрат по переменной

или

.

Приводя подобные, получим

; ;

.

Введем новые координаты и :

, .

Тогда последнее уравнение примет вид

.

А это - каноническое уравнение параболы с параметром и с вершиной в т. в системе . Выполним последовательное построение этой параболы (рис. 7).

Рис. 7

Пример 3. Привести к каноническому виду уравнение

.

Решение. Здесь . Вычислим . Данная линия принадлежит к эллиптическому типу. Прежде всего освободимся от членов с первой степенью переменных, для чего начало координат перенесем в центр данной линии. Его координаты найдем из системы:

Преобразование параллельного переноса будет иметь вид:

, . В этом случае . В системе уравнение линии приобретает вид (*).

Для освобождения от члена с произведением , проведем поворот координатных осей на угол . Его найдем из уравнения . Его решение и . Возьмем, например, первое значение . Тогда . Преобразование поворота будет иметь вид

,

.

Подставляя и в уравнение (*), получим

; .

Получили каноническое уравнение эллипса. Выполним последовательное построение этого эллипса (рис. 8).

Рис. 8