Задача №2

Даны координаты вершин пирамиды :

, , , . Найти:

1. длину ребра ;

2. угол между ребрами и ;

3. уравнение плоскости и угол между ребром

и плоскостью ;

4. уравнение высоты, опущенной из вершины на грань

и ее длину;

5. площадь грани и объем пирамиды.

Сделать чертеж.

Решение. 1) Длина ребра равна расстоянию между точками и :

.

2) Найдем координаты векторов, которые совпадают с выходящими из вершины ребрами пирамиды:

Угол между ребрами и равен углу между векторами и . Определим этот угол, используя формулу скалярного произведения векторов:

.

Отсюда

Тогда

.

3) Уравнение плоскости, проходящей через три заданные точки, имеет вид

.

Подставляя в уравнение координаты точек , и получим

,

или

.

Таким образом, уравнение плоскости имеет вид

или .

Составим уравнение прямой, проходящей через точки и . Уравнение прямой, проходящей через две точки, имеет вид

,

где – координаты первой точки, – координаты второй точки. Подставляя в уравнение координаты точек и , получим

.

Угол между прямой и плоскостью определяется по формуле

Воспользуемся этой формулой для вычисления угла между ребром и плоскостью :

Отсюда

.

4) Уравнение высоты найдем как уравнение прямой, проходящей через точку перпендикулярно плоскости , задаваемой уравнением . Из условия перпендикулярности прямой и плоскости следует , поэтому уравнение высоты имеет вид

.

Для нахождения длины высоты можно использовать формулу . Объем и площадь будут найдены в п.5). Поэтому .

5) Грань представляет собой треугольник, площадь которого равна половине площади параллелограмма, построенного на векторах и .

Найдем векторное произведение этих векторов. Имеем

.

.

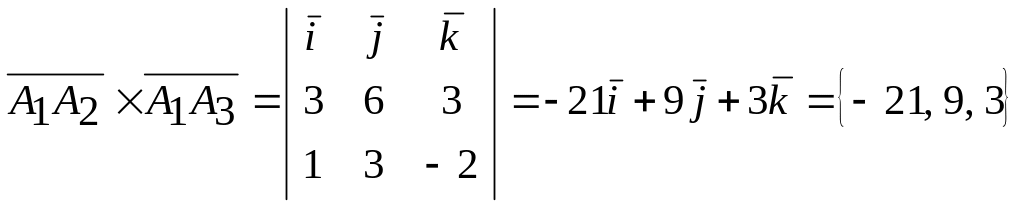Следовательно,

.

Для вычисления объема пирамиды воспользуемся смешанным произведением векторов. Напомним, смешанное произведение трех векторов по модулю равно объему параллелепипеда, построенного на этих векторах. А объем пирамиды равен части объема этого параллелепипеда. Имеем

.

Поэтому

.

Задача №3

Пример 1. Найти уравнение геометрического места точек, одинаково удаленных от начала координат и точки .

Решение. Пусть точка принадлежит искомой линии. Расстояние между точками и вычисляется по формуле

.

По условию задачи , поэтому . Возведем обе части уравнения в квадрат. Приводя подобные члены, получим . Это и есть уравнение искомого геометрического места точек. Рекомендуется проверить, что эта прямая перпендикулярна отрезку и проходит через его середину.

Пример 2. Найти уравнение геометрического места точек, каждая точка которой находится вдвое дальше от точки , чем от точки .

Решение. Пусть точка принадлежит искомой линии. По условию задачи

Найдем расстояния от точки до точек и

, .

Тогда

.

Возведем обе части уравнения в квадрат

.

Преобразуем это уравнение

,

.

Приведем это уравнение к каноническому виду, выделив полные квадраты

,

,

Это есть каноническое уравнение окружности с центром в точке и радиусом . Для изображения этой окружности сделаем параллельный перенос осей координат в точку . Чертеж в системе координат приведен на рис. 2.

Пример 3. Найти уравнение геометрического места точек, каждая точка которой равноудалена от точки и от прямой .

Рис. 2

Р

x

ешение. Пусть точка принадлежит искомой линии. Обозначим через расстояние от точки до этой прямой. По условию задачи

Для вычисления расстояния от точки до прямой воспользуемся формулой

.

Тогда

,

или

.

Возведем обе части уравнения в квадрат

,

,

Приведем это уравнение к виду .

,

,

.

Это есть каноническое уравнение параболы. Вершина параболы находится в точке , параметр , а ветви параболы направлены в положительную сторону оси . Для выполнения чертежа перенесем начало координат в точку . Тогда в системе координат парабола будет иметь вид (рис.3)

Рис. 3