3. Составим критериальную таблицу для другой полной системы функций из р2: {0, 1, x1x2, x1x2}.

	Т0	Т1	L	M	S
0	+	-	+	+	-
1	-	+	+	+	-
x1x2	+	+	-	+	-
x1x2	+	-	+	-	-

Согласно критериальной таблице, полной является и система {1, x₁x₂, x₁x₂}. Константа 0 введена в эту систему для удобства, тогда мы можем записать полином Жегалкина в виде, где а равны 0, если члены х х ...х , в полиноме отсутствуют.

4. Выясним, полна ли система . Составим критериальную таблицу, очевидно . Чтобы показать, что , достаточно найти одну функцию и . Возьмем , удовлетворяющую требуемым условиям. Если f S\T₀, то f(0, ..., 0) = 1, f(1, ..., 1)=0, следовательно, f M, f T₁. Рассмотрим функцию h = x₁x₂ x₂x₃ x₁x₃=1, набор ее значений (11101000), h S\T₀, но h L. Следовательно, критериальная таблица имеет вид:

	Т0	Т1	L	M	S
L T1	-	+	+	-	-
S\T0	-	-	-	+	-

и А – полная система функций.

Система функций {f₁, ..., f_s, ...} называется базисом в Р₂,если она полна в Р₂, но любая ее подсистема не будет полной. Например, система функций {x₁&x₂, 0, 1, x₁ x₂ x₃} – базис.

Контрольная работа

Вариант I

1. Составить таблицу истинности для булевой функции:

2. Составить СДНФ и СКНФ для:

3. Найти минимальную (сокращённую) ДНФ для в.ф. ы

4. Определить является ли следующая система функций полной {0,1,¬x, }

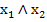5. Дана формула . Определите булевую функцию, которую реализует данная формула (составить таблицу истинности)

Вариант II

1. Составить таблицу истинности для булевой функции:

2. Составить СДНФ и СКНФ для:

3. Найти минимальную (сокращённую) ДНФ для в.ф. ы

4. Определить является ли следующая система функций полной

5. Дана формула 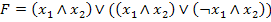. Определите булевую функцию, которую реализует данная формула (составить таблицу истинности)

Раздел 4. Предикаты и бинарные отношения.

Тема 4.1 Понятие предиката. Область определения и область истинности предиката.

Предикатом называется функция , где произвольное множество, а определённое двоичное множество .

Иначе говоря, местным предикатом, определённым на множестве называется двузначная функция от аргументов из произвольного множества . Множество называется предметной областью предиката, переменные - предметными переменными. В принципе, можно определить предикат как функцию , то есть допустить, что переменные принимают значения из различных множеств – в некоторых случаях это оказывается удобным.

Для любых и существует взаимно однозначное соответствие между местными отношениями и местными предикатами на множестве , определяемое следующим образом. Каждому местному отношению соответствует предикат такой, что тогда и только тогда, когда ; всякий предикат определяет отношение такое, что тогда и только тогда, когда . При этом задаёт область истинности предиката.

Всякой функции можно поставить в соответствие местный предикат такой, что тогда и только тогда, когда . Поскольку функция должна быть однозначной, то это соответствие требует, чтобы для любого выполнялось . Поэтому обратное соответствие (от предиката к функции) возможно только при выполнении указанного условия.

Пример 1.

а) Предикат является двухместным предикатом, предметной областью которого могут служить любые множества действительных чисел. Высказывание истинно, а высказывание ложно. Если вместо одной из переменных подставить число, то получится одноместный предикат: и так далее.

б) В описаниях вычислительных процедур и, в частности, в языках программирования, часто встречаются указания типа “повторять цикл до тех пор, пока переменные и не станут равными или прекратить вычисление цикла после ста повторений”. Если обозначить через счётчик повторений, то описанное здесь условие примет вид , а само указание в целом описывается выражением: “повторять, если ”.