Лекция 7. Непрерывная случайная величина и её распределения

Уточним определение непрерывной случайной величины.

Случайную величину Х назовем непрерывной, если её интегральная функция распределения непрерывна.

Класс непрерывных случайных величин, функции распределения которых всюду непрерывны и дифференцируемы, имеет и другую, удобную форму задания распределения, с помощью, так называемой функции плотности вероятности f(x), определяемой как предел

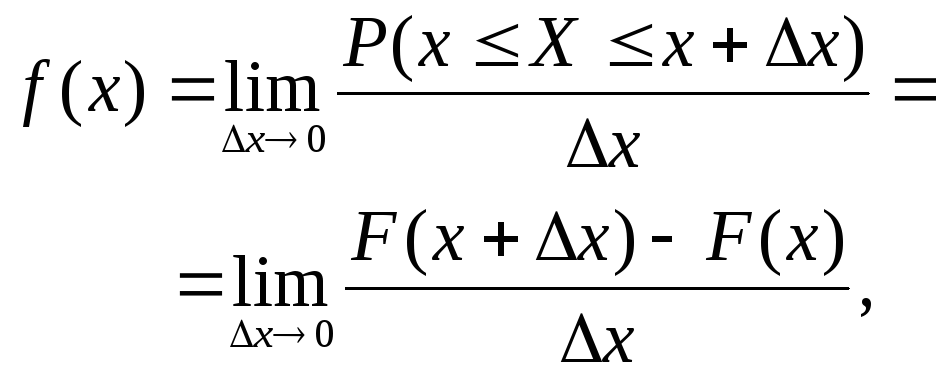
Или, что то же самое,

(1)

Из определения и свойств функции распределения следует

С учетом формулы (1), получим

(2)

В связи с введенными формулами, F(x) и f(x) получили названия интегральной и дифференциальной функций распределения соответственно.

Отметим один интересный факт: вероятность того, что непрерывная случайная величина примет какое-либо конкретное значение Х = а равна нулю:

Свойства функции плотности:

1. . Это свойство следует из того,F(x)-неубывающая функция.

2. ,

3. . Это свойство следует из формулы Лагранжа для функцииF(x).

В частности при малых значениях , приближенно выполняется равенство

.

4. .

Прокомментируем некоторые из этих свойств функции плотности:

Свойство 3) позволяет пояснить вероятностный смысл функции плотности. Так, предположив для определенности область возможных значений случайной величины Х конечной и разбив её на одинаковые, достаточно малые интервалы группированияс центрами в точках

и т.д.,

мы можем поставить в соответствие каждому i-му интервалу вероятность события

,

равную величине . Таким образом,значения функции f(x) пропорциональны вероятности того, что исследуемая случайная величина примет значения в непосредственной близости от точки х. Отсюда следует, что наиболее вероятным (модальным) значением случайной величины является такое значение , в котором функция плотности достигает своего максимума, т.е.

.

Геометрическая интерпретация свойства 2) непосредственно следует из геометрического смысла определенного интеграла.

Нормальное (гауссовское) распределение

Это распределение занимает центральное место в теории и практике вероятностно-статистических исследований. В качестве непрерывной аппроксимации к биномиальному распределению оно впервые рассматривалось А. Муавром еще в 1733 году. Некоторое время спустя нормальное распределение было снова открыто и изучено независимо друг от друга К. Гауссом (1809 г.) и П. Лапласом (1813 г.). Оба ученых пришли к нормальному закону в связи со своей работой по теории ошибок наблюдений. Идея их объяснения механизма формирования нормально распределенных случайных величин заключается в следующем. Постулируется, что значения исследуемой непрерывной случайной величины формируются под воздействием очень большого числа независимых случайных факторов, причем сила воздействия каждого отдельного фактора мала и не может превалировать среди остальных, а характер воздействия – аддитивный. Можно показать, что функция плотности распределения случайных величин подобного типа имеет вид

, (3)

где , а – любое действительное число. Само распределение называют нормальным. Проведя исследование функцииметодами дифференциального исчисления, легко убедиться, что её график имеет вид:

Рис. 7.1. график функции плотности нормального распределения

Найдем функцию нормального распределения. Запишем по определению (формула (2)):

.

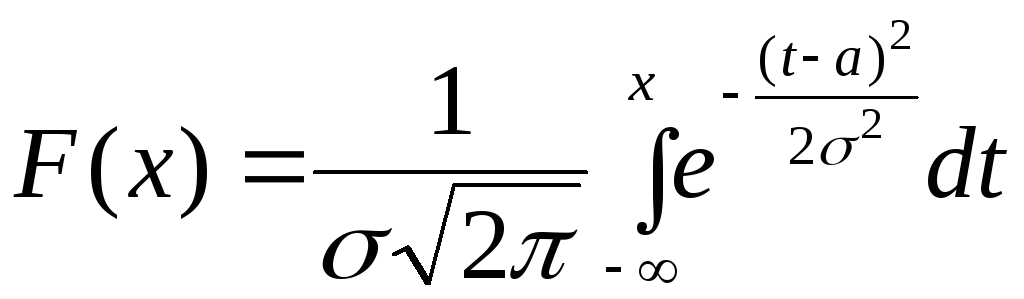Выполним замену переменной интегрирования по формуле

, .

Тогда интеграл примет вид:

.

Первый интеграл в полученной формуле есть интеграл Пуассона и равен

,

второй интеграл – значение интегральной функции Лапласа в точке :

.

Тогда

(4)

Как следствие из формулы (4) отметим следующие формулы:

(5)

(6)

В частности, если , то из формулы (6) следует

(7)

Формулу (7) часто называют «Правилом трех сигм», которое означает, что с достаточно большой вероятностью P = 0,9973, можно утверждать, что почти все значения случайной величины находятся в интервале с центром М(Х) = а и радиусом .