Общая_климатологияКн1

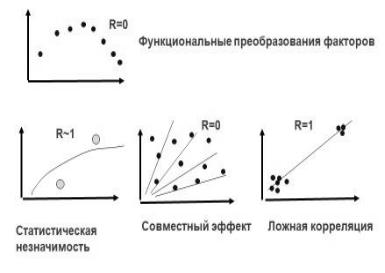
Рис. 3.19. Коэффициент корреляции при разной тесноте связи между переменными

На верхнем графике рис. 3.19 формально вычисленный R = 0, но зависимость является криволинейной и при функциональном преобразовании X, например, в X2, становится линейной и будет иметь значение R близкое к 1. На следующем графике коэффициент R очень высокий (R = 1), но рассчитан при малом объеме данных (n = 2) и его статистическая значимость очень низкая, т. к. в предельном случае через две точки всегда можно провести прямую. На графике посередине в нижнем ряду R = 0, но в данном случае имеет место влияние второго фактора в виде произведения с первым (совместный эффект), который формирует семейство прямых, и фактически коэффициент корреляции при двухфакторной зависимости будет высокий. На правом крайнем графике показан пример ложной корреляции при R = 1, но фактически имеют место две группы данных при больших значениях и малых значениях, которые искусственно объединены в одну зависимость. Если же рассматривать эти две группы данных по-отдельности, то связанность внутри них практически отсутствует. Поэтому, помимо формального расчета коэффициента корреляции, следует анализировать графические зависимости между переменными.

190

Аналитическая форма линейной взаимосвязи выражается уравнением, которое называется уравнением регрессии:

где: b1, b0, - коэффициенты уравнения регрессии.

Для вычисления коэффициентов уравнения регрессии применяют разные методы, но наиболее известным и популярным из них является метод наименьших квадратов (МНК), который минимизирует сумму квадратов отклонений от «истинной» линии. При применении МНК предполагается, что весь разброс точек относительно прямой линии обусловлен погрешностями в Y, а погрешности в X отсутствуют. Если учитывать погрешности ε, то уравнение (3.44) запишется следующим образом:

а сумма квадратов отклонений (SS) вычисляется как:

т. к. отклонения или остатки εi являются разностью между наблюденными и рассчитанными по (3.45) значениями зависимой переменной.

Получить минимальное значение SS можно путем дифференцирования уравнения (3.46) по b1 и b0 и приравнивания результатов дифференцирования к нулю. Тогда:

191

В итоге для вычисления коэффициентов b1 и b0 будут иметь место следующие формулы:

Если подставить в (3.48) формулу для расчета коэффициента корреляции (3.43), то получим более простое выражение для b1:

где: Sy и Sx – средние квадратические отклонения рядов Y и X.

Геометрическая интерпретация коэффициентов, исходя из формул (3.48) и (3.49), состоит в том, что коэффициент b1 представляет собой отношение градиента Y (или Sy) к градиенту X (или Sx), что является тангенсом угла наклона прямой линии, представленной (3.44), а коэффициент b0 равен значению Y при X = 0, что соответствует пересечению прямой (3.44) вертикальной оси.

Определение коэффициентов b1 и b0 по МНК не всегда корректно, особенно в климатологии, где погрешности содержатся не только в отклике, но и в факторах. Поэтому расчетные значения Y, полученные по (3.44), следует корректировать или применять другие методы расчета коэффициентов, например:

-метод единого решения или однозначной аппроксимации, когда минимизируются остатки как по Y, так и по X, что соответствует минимизации прямоугольника отклонений от линии регрессии;

-метод ортогональной регрессии, когда минимизируются перпендикуляры отклонений от линии регрессии.

Графическая интерпретация разных методов минимизации остатков для вычисления коэффициентов уравнения регрессии приведена на рис. 3.19, включая МНК, единое решение, ортогональную регрессию, метод абсолютных отклонений.

192

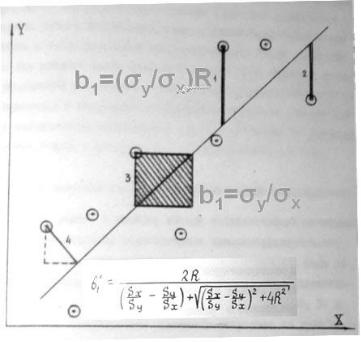
Рис. 3.20. Графическая интерпретация методов расчета коэффициентов уравнения регрессии, где номера для остатков: 1 – МНК, 2 – метод абсолютных отклонений, 3 – однозначная аппроксимация, 4 – ортогональная регрессия

Фактически минимизация отклонений или по оси Y или по оси X приводит к тому, что имеют место две зависимости: Y = f(X) и X = f(Y), приведенные на рис. 3.21 в виде Y1 = g(Y2) и Y2=g(Y1), где Y1 – рост людей, Y2 – их вес. Если МНК используется для минимизации остатков Y2, то имеет место прямая линия Y2 = g(Y1), если же считается, что погрешности имеют место только в Y1, то получаем прямую Y1 = g(Y2). Фактически же зависимость должна быть одна и учитывать погрешности, как в факторе, так и в отклике. Разброс точек на рис. 3.21 можно представить в виде эллипса рассеяния. Тогда зависимости Y1 = g(Y2) и Y2 = g(Y1) являются диагоналями этого эллипса или «ножницами» регрессии. Если провести прямую линию между этими диагоналями, то получим главную диагональ эллипса рассеяния, соответствующую методу однозначной аппроксимации.

193

Рис. 3.21. Зависимости Y2 = g(Y1) и Y1 = g(Y2) при разных условиях МНК

Оценка эффективности уравнения и множественная регрессия

Как и все статистические параметры, коэффициенты уравнения регрессии и расчетные значения также определяются по выборке и имеют случайные погрешности. Также, если доверительный интервал коэффициентов уравнения включает нулевое значение, то они являются статистически незначимыми.

Случайная средняя квадратическая погрешность коэффициента b1 вычисляется по формуле:

где: Sb1 – средняя квадратическая погрешность коэффициента b1, Sε

– средняя квадратическая погрешность остатков.

Тогда «истинное» значение коэффициента b1, которое обозначим β1, будет находиться в доверительном интервале:

194

где: t – ордината t-распределения, при n-2 степенях свободы и заданном уровне значимости α в долях 1.

Формула (3.52) применяется и для оценки статистической значимости коэффициента b1, который будет незначимым, если интервал (3.52) включает нулевое значение.

Случайная средняя квадратическая погрешность коэффициента b0 вычисляется по формуле:

а «истинное» значение коэффициента β0 будет внутри доверительного интервала:

Случайные погрешности имеют место также и в расчетных значениях Y, определенных по уравнению (3.44). Стандартная погрешность расчетного по уравнению k-го значения (Ypk) вычисляется по формуле:

где: Xk – k-ое значение фактора.

Доверительный интервал расчетного значения Ypk также вычисляется через ординаты t-распределения, но эти доверительные интервалы являются не прямыми линиями параллельными аналитической прямой, а гиперболами, т. е. доверительные интервалы

195

расширяются в областях малых и больших значений, т. к. точность на краях облака рассеяния меньше.

Точность оценки полученного уравнения линейной регрессии можно определить, если рассмотреть следующее тождество:

где Yi-Yip – остатки εi, Yi-Yср – отклонение фактического значения от среднего, Yip – Yср – отклонение расчетного значения от среднего.

Если возвести обе части (3.56) в квадрат, то после несложных преобразований и перестановки слагаемых получим основное уравнение дисперсионного анализа при разложении суммы квадратов (SS) отклонений относительно среднего на сумму квадратов, обусловленную регрессией и сумму квадратов остатков:

где: Σ(Yi-Yср)2 – сумма квадратов относительно среднего, Σ(Yi-Yip)2 – сумма квадратов относительно регрессии, Σ(Yip–Yср)2 – сумма квадратов, обусловленная регрессией.

Из (3.56) следует, что эффективность уравнения регрессии зависит от того, какая часть исходной суммы квадратов (относительно среднего) приходится на сумму квадратов, объясненную уравнением регрессии. Уравнение регрессии можно признать эффективным, если SS, обусловленная регрессией, будет много больше, чем SS, относительно регрессии (остатки) или, что тоже самое, если отношение R2 = Σ(Yip–Yср)2 / Σ(Yi-Yср)2, будет не слишком сильно отличаться от единицы, где R2 – коэффициент детерминации или коэффициент корреляции в квадрате. Поэтому, чем больше исходного разброса объясняет уравнение регрессии, тем оно эффективнее и тем выше коэффициент детерминации и если его выразить в %, то он характеризует долю исходного рассеяния, объясненную уравнением. Так, если, например, коэффициент корреляции R = 0,8, то коэффициент детерминации R2 = 0,64 и это зна-

196

чит, что уравнение объяснило 64% исходного разброса относительно среднего значения.

Вместе с тем, всякая сумма квадратов связана с числом степеней свободы, которое показывает, как много независимых элементов информации, получающихся из n независимых Yi требуется для образования данной суммы квадратов. Например, для SS относительно среднего требуется n–1 независимый элемент. Для SS, обусловленного регрессией используется только один коэффициент b1 и число степеней свободы также будет равно 1. Тогда по разности SS относительно регрессии (SS остатков) имеет n–2 степени свободы. В результате можно построить таблицу дисперсионного анализа (табл. 3.3).

Средний квадрат в табл. 3.3 получается при делении каждой суммы квадратов на соответствующее ей число степеней свободы.

Простая или однофакторная регрессия является частным случаем множественной линейной регрессии, которая широко применяется как в гидрометеорологии, так и в других науках. Уравнение множественной регрессии с несколькими факторами имеет следующий стандартный вид:

197

По своей структуре это уравнение является аддитивным, т. е. факторы влияют на отклик независимо и не связаны между собой. Вместе с тем могут иметь место и другие структуры уравнений. В случае, если один фактор влияет на другой, то это влияние выражается в виде произведения факторов, и структура уравнения будет мультипликативной:

В действительности же одновременно могут иметь место как совместные эффекты в виде произведений факторов, так и аддитивное воздействие отдельных независимых факторов, и тогда структура уравнения будет смешанная с совместными эффектами:

Помимо совместных эффектов часто необходимы и функциональные преобразования факторов, например, логарифмические или степенные, чтобы преобразовать криволинейную зависимость в прямолинейную, т. е. произвести ее линеаризацию. Поэтому наиболее общей является структура регрессионного уравнения с совместными эффектами и функциональными преобразованиями факторов:

Литература

1.Вентцель Е.С. Теория вероятностей. — Изд. 4-е, стереотипное. — М.:

Наука, 1969. — С. 17.

2.Лобанов В.А., Смирнов И.А., Шадурский А.Е. Практикум по климатологии.

Часть 1. (учебное пособие). СПб., 2011. – 144 с.

3.Малинин В.Н. Статистические методы анализа гидрометеорологической информации. – СПб.: РГГМУ, 2008. – 408 с.

4.Химмельблау Д. Прикладное нелинейное программирование. Изд. Мир,

1975. – 536 с.

198

Лекция 4. Оценка однородности и стационарности

4.1. Причины неоднородности

Прежде, чем приступать к климатической обработке рядов наблюдений, которая состоит в расчете параметров распределения и определении климатических характеристик редкой повторяемости, необходимо убедиться, что информация является надежной и качественной или однородной по статистической трактовке. В зависимости от того, что будет заложено в эту своеобразную «мясорубку» математических вычислений по обработке информации, такой по качеству и надежности получится и результат, т. е. работает принцип: «Что заложим, то и получим». Поэтому оценка однородности климатических многолетних рядов наблюдений является первой необходимой процедурой, которая выполняется перед обработкой. Причины нарушения однородности могут быть как естественными, так и связанными с приборами и человеческим фактором.

Естественные причины нарушения однородности климатических характеристик связаны с естественной климатической изменчивостью и изменением климата. Обычно считается, что климатическая изменчивость носит случайный характер, хотя имеет место цикличность, выраженная в группировании периодов, связанных с преобладанием определенных типов атмосферной циркуляции. Так, теплые зимы на Европейской территории России связаны с преобладанием западного переноса воздуха из Средней и Северной Атлантики, а холодные зимы – с приходом воздушных масс из Арктики и Сибири (северный и северо-восточный перенос воздуха). Вместе с тем, за многолетний период в 100–150 лет циклы повышенной и пониженной зимней температуры компенсируют друг друга, поэтому можно считать, что колебания хотя и представлены цикличностью, но параметры этих циклов, вызванных климатической изменчивостью, случайны. Аналогичные циклические колебания имеют место и в таком известном отклике климатической системы, как Эль-Ниньо, представляющем собой положительные аномалии температуры воды в экваториальной части Тихого океана.

199