Общая_климатологияКн1

Вторым по точности и наиболее распространенным в практике методом оценки выборочных параметров распределения вероятностей является метод моментов, предложенный К. Пирсоном в 1894 г. Идея метода заключается в замене параметров генеральной совокупности их выборочными аналогами. При этом составляется столько уравнений, сколько неизвестных параметров требуется оценить и выбираются те моменты, которые выражаются через неизвестные параметры.

Моментом распределения (М) называется средняя арифметическая из отклонений значений признака x от величины a в степени k. Порядок момента определяется величиной степени k. Моменты бывают условные (эмпирические), начальные и центральные, а также смешанные.

Эмпирический момент k-го порядка определяется по формуле:

где f – весовой коэффициент и при равных весовых коэффициентах f=1 сумма Σf=n – объему выборки.

Если a = 0, то момент называется начальным и определяется по формуле:

а при a = xср (среднее значение) момент называется центральным и вычисляется как:

Методом моментов оценки четырех основных параметров распределения: среднее значение (хср), дисперсия (s2), коэффициент асимметрии (Cs) и коэффициент эксцесса (В), соответствую-

170

щие первым четырем моментам распределения, определяются по формулам для выборки объема n:

Помимо этих основных параметров распределения на их основе вычисляется и ряд других, например, коэффициент вариации

Cv:

среднее квадратическое отклонение (СКО):

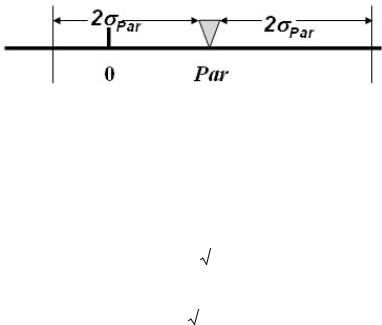
Формулы (3.27)–(3.29) можно выразить также и через модульные коэффициенты Ki = xi/xср и, например, для коэффициента асимметрии Cs формула будет иметь вид:

171

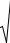
Примером смешенного момента является коэффициент корреляции между двумя переменными или автокорреляции между смежными членами ряда (r(1)) при сдвиге ряда на 1, который определяется по формуле:

где: xср1 – среднее, рассчитанное по ряду x1 до xn-1, а xср2 – среднее по ряду, сдвинутому на 1 от x2 до xn.

Еще одним методом расчета параметров распределения является метод квантилей. Сущность метода схожа с методом моментов: выбирается столько квантилей распределения, сколько требуется оценить параметров. При этом неизвестные теоретические квантили, выраженные через параметры распределения, приравниваются к эмпирическим квантилям. Решение полученной системы уравнений дает искомые оценки параметров. Метод квантилей позволяет получить асимптотически нормальные оценки, однако они несут в себе некоторый субъективизм, связанный с относительно произвольным выбором квантилей. Эффективность оценок не выше метода моментов. Определение оценок может приводить к необходимости численного решения достаточно сложных систем уравнений.

Оценки, вычисленные на основе различных методов, различаются. Универсального ответа на вопрос, какой из рассмотренных методов лучше или следует ли положиться на данный метод при решении любой задачи, нет. Значение оценки в каждом конкретном случае (для разных выборок) отличается от истинного значения параметра на неизвестную величину, иначе говоря, существует некоторая доля неопределенности в знании действительного значения параметра. Качество оценок можно определить косвенно путем проверки согласованности эмпирических данных и теоретического закона распределения.

172

Основная особенность оценки параметров любым методом состоит в том, что они вычисляются с погрешностями и находятся внутри интервала, в котором с заданной степенью достоверности будет заключено истинное или генеральное значение оцениваемого параметра. Такая интервальная оценка характеризуется двумя числами – концами интервала, внутри которого предположительно находится истинное значение параметра. Иначе говоря, вместо отдельной точки для оцениваемого параметра можно установить интервал значений, одна из точек которого является своего рода "лучшей" оценкой. Интервальные оценки являются более полными и надежными по сравнению с точечными, они применяются как для больших, так и для малых выборок. Совокупность методов определения промежутка, в котором лежит значение параметра Par, получила название методов интервального оценивания.

Наиболее известным является метод Неймана по определению доверительных интервалов, основанных на случайной погрешности конкретного параметра (рис. 3.11).

Рис. 3.11. Интервальная оценка параметров

Случайная стандартная или выборочная (за счет ограниченного объема выборки) погрешность для каждого параметра определяется по своей формуле. Для среднего значения, СКО, коэффициента асимметрии и автокорреляции имеют место следующие приближенные формулы определения стандартной случайной погрешности:

Как правило, доверительный интервал относительно вычисленного выборочного параметра включает удвоенную стандартную погрешность или иначе его называют 2х-сигмовым (2σ-вым) доверительным интервалом или 95%-ным доверительным интервалом, т. к. по правилу трех сигм для нормального распределения 2х-сигмовый интервал включает примерно 95% площади всего распределения. Тогда с вероятностью 95% следует, что истинное значение рассматриваемого параметра (Par) лежит внутри следующего доверительного интервала:

Если же говорят о 99%-ном доверительном интервале, то имеют в виду интервал тройной стандартной погрешности (3σвый).

Еще одна особенность доверительного интервала состоит в том, что с его помощью оценивается статистическая значимость параметров и любой статистики, вычисленной по выборочным данным. Если доверительный интервал, определенный, например, по (3.37), включает нулевое значение, то параметр является статистически незначимым.

Более точно доверительные интервалы погрешностей вычисляются, например, с помощью t-распределения и в этом случае выборочная погрешность среднего значения (Δxср) имеет вид:

где t – ордината t-распределения зависящая от принятой доверительной вероятности Р и числа измерений п.

174

Аналогичным образом t-распределение применяется для оценки статистической значимости коэффициента автокорреляции при наличии зависимости между r(1) и t:

«Практикума по климатологии. Часть 1» для доверительной вероятности 95% и 99% c n-2 степенями свободы.

Таким образом, параметры генеральной совокупности могут быть известны только на основании теоретических соображений. Однако можно определить область в которой будет находится статистика, полученная по выборке. Для этого около теоретического значения параметра определяется доверительный интервал, внутри которого должна с заданной вероятностью находится выборочная статистика. Границы интервала называются допустимыми границами и предложены А. Вальдом и Дж. Вольфовицем.

Нуль-гипотеза и альтернативная гипотеза

Гипотезой в математической статистике называется научное предположение, которое необходимо проверить, а далее принять или отвергнуть. Нулевой гипотезой является теоретическое утверждение, постулирующее отсутствие различий между сравниваемыми величинами (выборками) или отсутствие связи между изучаемыми переменными. При этом предполагается, что действительное различие равно нулю, а установленное из эксперимента отличие от нуля носит случайный характер. Нулевая гипотеза считается верной до того момента, пока она не будет опровергнута, т. е. пока не будет доказано обратное. Нулевая гипотеза обычно обозначается как Н0.

При статистическом выводе исследователь пытается показать несостоятельность нулевой гипотезы, несогласованность её с имеющимися опытными данными, то есть отвергнуть гипотезу. При этом подразумевается, что должна быть принята другая, альтернативная (конкурирующая), исключающая нулевую гипотезу,

175

которая обозначается как Н1. Если же данные наоборот подтверждают нулевую гипотезу, то она не отвергается. Это похоже на принцип презумпции невиновности, когда подозреваемого считают невиновным (подразумевается нулевая гипотеза), пока не будет доказано обратное (нулевая гипотеза отвергнута).

Утверждение, сформулированные в нулевой и альтернативной гипотезах, относятся к параметрам генеральной совокупности, а решение принять или отклонить нулевую гипотезу принимается на основе численного критерия, рассчитанного по выборке, т. е. с ошибками. Поэтому отвергнуть нулевую гипотезу и принять альтернативную можно только тогда, когда отличие не носит случайного характера. Для решения, является ли это различие случайным или значимым, требуется установить границы, где проявление случайности, как правило, заканчивается. Такими границами может быть достаточно высокая вероятность принятия нулевой гипотезы, например, 95% или 99%, что по правилу трех сигм соответствует 2х и 3х сигмовому интервалу.

Общий алгоритм проверки любой нулевой гипотезы включает в себя следующие шаги:

1)Требуется сформировать нулевую гипотезу. Например, нулевой гипотезой является равенство дисперсий двух последовательных и равных частей временного ряда наблюдений за температурой воздуха.

2)Получение фактических данных о событиях, относительно которых была сформирована нулевая гипотеза. В данном случае – это расчет дисперсий для каждой из двух частей временного ряда и определение статистики некоторого критерия, например, известного критерия Фишера являющегося отношением двух дисперсий.

3)Определение вероятности того, что полученный результат мог быть получен в случае, когда нулевая гипотеза верна. Здесь необходимо задать высокую вероятность принятия нулевой гипотезы, например, в 95% или 99%.

4)Если вероятность получения данного результата мала, отвергаем нулевую гипотезу при уровне значимости, равном этой вероятности. Для этой цели выборочное значение статистики критерия сравнивается с тем, которое получено по генеральной совокупности при аналогичных объемах выборок. И если расчетное значение

176

больше критического, то в этом случае нулевая гипотеза отклоняется, а если меньше критического, то нулевая гипотеза принимается также с заданной вероятностью.

5) Признаем, что принимая или отвергая нулевую гипотезу, мы подвергаем себя определенному риску.

Таким образом, проверка любой гипотезы связана с применением статистического критерия, т. е. такого метода, который для каждой выборки определяет, удовлетворяет она нулевой гипотезе или нет. Многие критерии предполагают, что наблюдения независимы, как это имеет место в случайной выборке. Большинство статистических критериев используют статистику, которая является строгим математическим правилом для нахождения какого-либо числа по выборке. Тогда критерий состоит в том, что решение принимается согласно этой статистике. По своей структуре или формуле критерии делятся на параметрические, которые содержат в формуле параметры распределения, и непараметрические, которые включают другие характеристики выборки, например, частоты, экстремумы, размах, но не статистические параметры.

Риски 1-го и 2-го рода, уровень значимости

При проверке гипотез по критериям возможны два ошибочных решения:

-неправильное отклонение нулевой гипотезы (ошибка 1-го рода или ложноположительное решение);

-неправильное принятие нулевой гипотезы (ошибка 2-го рода или ложноотрицательное решение).

Втоже время сама нулевая гипотеза может быть верна или неверна. В результате возможны четыре варианта решения, как показано в табл. 3.2.

177

Таблица 3.2

Варианты решения и фактическая оценка нуль-гипотезы

В случае проверки однородности или статистического равенства дисперсий двух частей временного ряда возможны следующие ситуации:

-если нулевая гипотеза о статистическом равенстве дисперсий верна, и она принимается, то получаем правильное решение;

-если нулевая гипотеза о статистическом равенстве дисперсий верна, но она отклоняется, то получаем ошибку 1-го рода;

-если нулевая гипотеза о статистическом равенстве дисперсий неверна, и она принимается, то получаем ошибку 2-го рода;

-если нулевая гипотеза о статистическом равенстве дисперсий неверна, и она отклоняется, то получаем правильное решение.

Вероятности, соответствующие обоим неверным решениям, называются риском I и риском II. Вероятность риска I (ошибка 1- го рода) называется уровнем значимости α и она должна быть очень маленькой, например, 0,05 (5%) или 0,01 (1%). Тогда область принятия нулевой гипотезы будет иметь вероятность P=1–α (рис. 3.12).

Вероятность принять неверную нулевую гипотезу называется риском II (ошибка 2-го рода) и обозначается буквой β. При заданных α и объеме выборки n значение β будет тем больше, чем меньше принятое α. При очень больших объемах выборок α и β будут очень малыми. При очень же малом объеме выборок и малом α возможность установить фактически существующее различие мала.

178

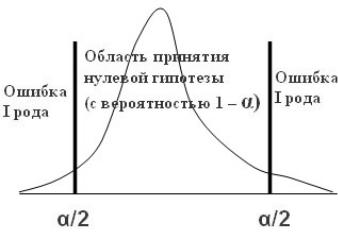
Рис. 3.12. Уровень значимости и область принятия нулевой гипотезы

Ошибка 2-го рода непосредственно связана с существованием распределения альтернативной гипотезы (Н1). При α = β между нулевой и альтернативной гипотезой появляется симметрия. Нередко тщательно выбирают только значение α, не обращая внимания на симметрию и ставя нуль-гипотезу в особое положение.

Уровень значимости требуется установить перед проверкой нулевой гипотезы. И если, например, задан уровень значимости

α= 0,05 (или 5%), то это означает, что в пяти случаях из ста мы рискуем допустить ошибку 1-го рода (отвергнуть правильную гипотезу). Часто задание уровня значимости является достаточно сложной задачей выбора и поэтому принято задавать α = 0,05 в большинстве случаев. Макнимар, например, предлагал, отклонять нулевую гипотезу при α < 0,01 (или < 1%) и принимать ее, если

α> 0,10 (или > 10%), а в интервале при 0,01 < α < 0,10 воздержаться от заключения и повторить эксперименты для получения большего числа данных. В общем можно выделить две различные стратегии принятия или отклонения нулевой гипотезы: стратегию «первооткрывателя» и «критика». «Первооткрыватель» хочет отвергнуть нулевую гипотезу, поэтому он предлагает большой риск I и большой уровень значимости α = 0,10. Для «критика» справедливо обратное, и он до последних сил держится за нулевую гипотезу и соглашается ее отклонить только при очень маленьком

179