892

скоростях V1, V2, V3, то при трех повторностях и наличии эталонной машины необходимо провести 18 опытов, для которых будет необходимо 18 делянок шириной примерно в 8…10 захватов (настройка, тщательная регулировка, определение агротехнических показателей, энергетическая оценка машины и ее рабочих органов).

После рандомизации (которую можно осуществить на компьютере, по таблице случайных чисел или просто перетасовав карточки с вариантами), схема расположения участков (делянок) может оказаться следующей (табл. 6.1), где введены обозначения: «э» - эталонная, а «и» - испытуемая машины.

Таблица 6.1

Схема расположения делянок

В некоторых случаях на реализацию опытов могут быть наложены ограничения с целью получения более сопоставимых результатов. Например, исследуется работа новой сеялки, но эффективность ее работы зависит от агрегата, в котором используется (одно-, двухили трехсеялочный агрегат). В этом случае опыты разбивают на блоки (допустим А, В, С, а затем случайным образом размещают блоки и опыты внутри них (табл.6.2).

Таблица 6.2

Вариант блочного плана размещения делянок

Даже беглый анализ плана показывает, что если сопоставимость по строкам обеспечивается, то по столбцам она не выполняется. В первом столбце не испытываются агрегаты на скорости V1, во втором – V2, в чет-

вертом V3.

Если поле не выравнено по каким-либо параметрам и нужно стремиться к полной сопоставимости по продольному и поперечному направлениям, то необходимо использовать планы, составленные по латинскому квадрату, в такой схеме все элементы в строках и столбцах повторяются один раз (табл.6.3)

181

мание крупные столбцы А, В, С, то сопоставимость обеспечена. Поскольку внутри крупных столбцов большие отличия в свойствах почвы маловероятны, то потери от полной сопоставимости не будут очень значительными.

В последнее время, наряду с латинскими прямоугольниками, для планирования полевых опытов широко используются квадраты Юдена и так называемые BIB-планы (сбалансированные неполноблочные планы).

Эти планы представляют собой часть латинского квадрата (неполные латинские квадраты), и полной сопоставимости они обеспечить не могут. Чтобы не слишком ухудшить это важное свойство латинского квадрата, в BIB-планах элементы сбалансированы, т.е. встречаются одинаковое число раз и входят во взаимодействие со всеми элементами плана.

Например, латинский квадрат из четырех элементов может представить собой план:

Таблица 6.5.

План четырехфакторного эксперимента по схеме латинского квадрата

Если предположить, что четырехкратная повторность излишняя, и есть желание ее сократить до трех, или двукратной, то оставшиеся части будут представлять собой планы «а» и «б»

План «а» оказался сбалансированным, так как каждый элемент А, В, С, Д встречается по столбцам со всеми отдельными по два раза (т.е. одинаковое число раз).

План «б» уже не сбалансирован, так как элемент А, например, встречается в одном столбце с В и Д, но не встречается с С.

Перечень BIB-планов и квадратов Юдена приводится в литературе по методикам полевого опыта [44], [45].

183

6.2.2. Планирование многофакторного эксперимента

Во введении книги «Планирование эксперимента при поиске оптимальных условий» Ю.П. Адлер – один из основных ученых нашей страны в этой области знаний, – не без иронии отмечает: «Мысль о том, что эксперимент можно планировать, восходит к глубокой давности.

Наш далекий предок, убедившийся, что острым камнем можно убить даже мамонта, несомненно, выдвигал гипотезы, которые после целенаправленной экспериментальной проверки привели к созданию копья, дротика, а затем и лука со стрелами. Он, однако, не пользовался статистическими методами, поэтому остается непонятным, как он вообще выжил, и обеспечил тем самым наше существование.

Только в начале 20-го века люди, наконец, поняли, что дальше так дело не пойдет, и придумали статистические методы планирования эксперимента. Часть открытия этой идеи принадлежит английскому статистику Рональду Фишеру, который впервые показал целесообразность одновременного варьирования несколькими факторами в противовес широко распространенному однофакторному эксперименту [46].

Шутка-шуткой, но, действительно, основой экспериментальной работы был однофакторный эксперимент. Причиной этого являлось изучение точными науками систем, в которых можно было выделить явления, зависящие от совсем малого числа переменных.

Полученные результаты описывались легко объяснимыми функциональными зависимостями, которым приписывалась роль абсолютных законов. При этом предполагалось, что поддерживая с достаточной точностью постоянными независимые переменные и изменяя последовательно первый, второй и т.д. факторы, исследователь может отыскать интересующую его зависимость. Переменные, которые исследователь не мог поддерживать на определенном уровне, чаще всего отбрасывались (оставляли без внимания) как несущественные.

Например, основное уравнение молотильного аппарата В.П. Горячкин вывел на основе теории неупругого удара и представил так:

где N2 – мощность, затрачиваемая на обмолот;

m – величина подачи хлебной массы в секунду; f – коэффициент сопротивления деки;

J – момент инерции барабана; ω – угловая скорость барабана;

d – допустимое ускорение барабана.

dt

По воспоминаниям акад. И.И. Артоболевского, когда В.П. Горячкин заканчивал вывод этой формулы на доске, он отходил от нее и резюмировал, что, мол, вот и все, что тут уже не добавить, не убавить ничего нельзя, что формула описывает весь процесс обмолота.

Как-то на лекции по молотильному аппарату студентам, уже порабо-

184

тавшим на комбайне во время производственной практики, был задан вопрос: «Не смогли бы вы назвать параметры технологического процесса обмолота, которые не учитывает данная модель?». Тут же было названо полтора десятка таких факторов. Это, например, вид культуры, влажность хлебной массы, степень соломистости, параметры молотильного аппарата и деки, зазоры между барабаном и декой и т.д.

Если считать, что каждый фактор нужно исследовать на р уровнях (допустим, в трех точках, чтобы можно было воспроизвести кривую линию,

отражающую зависимость), то число опытов определяется уравнением:

N = рm,

где m – число факторов; р – число уровней.

Несложно было посчитать, что N = 315 = 14348907.

Допустим, что на опыт затрачивается минимальное время, всего по 5 минут, тогда исследование займет 71744535 минут, что соответствует 1195742,25 часам, или 49822,594 суткам, или 136,5 года непрерывной работы.

Но в настоящее время изучаются процессы с гораздо большим числом факторов. Так, С.В. Мельников, изучая процесс измельчения сельскохозяйственных продуктов в молотковой дробилке, учитывал уже 27 факторов [47]. Таким образом, совершенно необходимы другие методы изучения многофакторных моделей.

Для того чтобы представить самый простой вариант, позволяющий во время опыта одновременно изменять не один, а сразу несколько факторов, представим искомую зависимость

Y = f(x1, x2,…,xn) (6.1) c геометрическим образом в виде некоторой поверхности, которую, в слу-

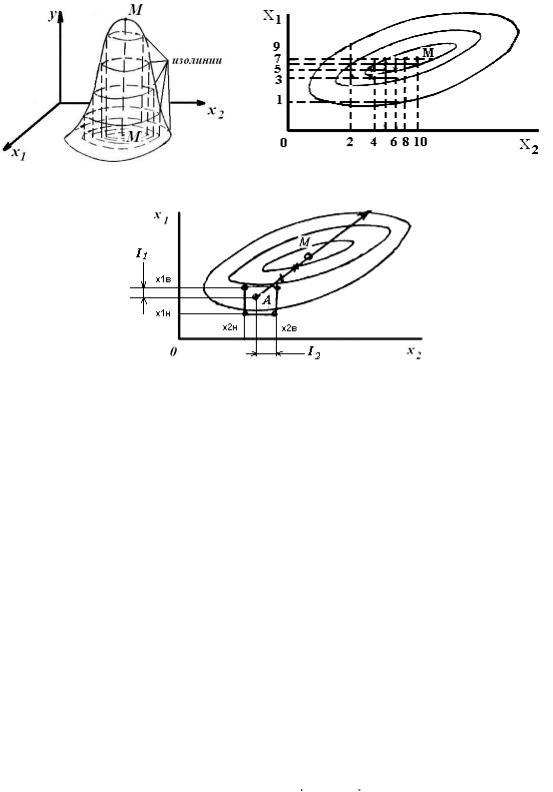
чае двухфакторного эксперимента, можно изобразить в трехмерном пространстве (рис. 6.1). Для двухфакторного эксперимента нет даже необходимости перехода к трехмерному пространству (рис. 6.1а). Поверхность можно представить в виде изолиний (рис.6.1б, в), как изображают горы и впадины на географических картах.

При большем числе факторов необходимо будет представлять поверхность в n-мерном пространстве как некоторую аналогию.

Вид поверхности отклика может быть самым разнообразным. В теории планирования эксперимента лишь принимают допущение о том, что она непрерывна в области определения, и имеет в ней единственный оптимум.

Поиск оптимальной точки М может быть осуществлен двумя способами. До недавнего прошлого классическим признавался метод ГауссаЗейделя. Он состоит в том, что сначала последовательно с некоторым шагом варьирования изменяют один фактор (допустим х2 (рис. 6.1б) при постоянном значении другого (допустим, х21). При этом находят и фиксируют наилучшее значение этого фактора. Фиксируют это значение х21, и последовательно меняют фактор х1. Находят оптимальное значение этого сечения, фиксируют х12 на оптимальном уровне и вновь меняют значение х2 (уже в другом сечении). Если эти действия продолжить, то в точку М эксперимен-

185

татор попадает неизбежно, но количество опытов очень велико.

В последнее время более эффективным считается шаговый принцип движения к оптимуму (метод Дж. Бокса и К. Уилсона).

в)

Рис. 6.1. Поверхность отклика многофакторного эксперимента

В этом случае на поверхности отклика (т.е. в факторном пространстве) выбирают произвольную точку А и проводят вокруг этой точки эксперимент на некотором расстоянии от нее. Это расстояние называют интервалом варьирования Ij, составляющим от 10 до 30% от предела изменения соответствующего фактора. Иными словами, эксперименты проводят в точках:

х1верхнее = хА + J1; x1нижнее = хА - J1; x2верхнее = х2А + J2 и х2нижнее = х2А - J2.

По результатам опытов определяют направление, по которому можно приближаться к оптимуму. В этом направлении и проводят последующие опыты.

Для сокращения числа опытов желательно, чтобы в зоне точки А первоначальных опытов было указано направление, в котором параметр оптимизации будет изменяться быстрее всего. Часто и сам метод Бокса-

Уилсона называют методом крутого восхождения.

Из векторного анализа известно, что направление самого быстрого изменения функции определяется ее вектор-градиентом.

Градиент функции отклика y = f(x1, x2,…, xn) в любой точке факторного пространства определяется выражением

186

факторов (орты).

Предположение о том, что функция отклика является непрерывной и дифференцируемой, дает возможность линеаризировать ее в ограниченной области (например, вокруг точки А), используя для этого формулу Тейлора:

Если учесть, что частные производные, вычисленные около определенной точки А, являются постоянными величинами, и сгруппировать все постоянные величины, то после некоторых преобразований можно будет получить:

Это уравнение называют уравнением регрессии, а b – коэффициентами регрессии. Эти коэффициенты зависят в основном от частных производ-

Если сравнить уравнение регрессии (6.3) с уравнением векторградиента (6.2), то нетрудно убедиться, что координаты вектор-градиента равны соответствующим коэффициентам регрессии в виде полинома первой степени, который аппроксимирует поверхность отклика вблизи точки

А.

В случае, когда коэффициенты удастся по первой серии опытов вокруг точки А найти, и проверить их значимость (они не должны быть сопоставимыми с ошибками опытов), то в последующем можно вести опыты с движением по градиенту.

Если один из факторов (допустим, х1) менять с некоторым шагом, то другие факторы нужно изменять в этом же опыте пропорционально соответствующим коэффициентам:

т.е. опыт вести так, как рекомендовал Р.Фишер, одновременно меняя значения всех факторов на величину хi.

В этом случае каждый из пары координат нового опыта окажется на вектор-градиенте. После некоторого количества шагов можно будет обнаружить максимальное значение (точка М).

187

6.2.3. Планы полного факторного эксперимента (ПФЭ)

При проведении начальной серии опытов вокруг начальной точки А (рис.6.1в) необходимо эксперимент выполнить при всех возможных сочетаниях факторов и их уровней (верхний и нижний). Такое исследование называется полным факторным экспериментом (ПФЭ).

Необходимо еще раз обратить внимание на то, что для линейной мо-

дели опыт достаточно провести только для двух уровней хверх и хниж, поскольку прямую линию можно провести по двум экспериментальным точ-

кам.

При небольшом количестве факторов подобрать все возможные сочетания факторов и их уровней еще возможно. Но если факторов много, то задача становится очень сложной. Выход из этого затруднения находят в

хj – натуральное значение j-го фактора (верхнее или нижнее); хjA – натуральное значение основного уровня j-го фактора.

Нетрудно убедиться, что все кодированные значения верхних уровней факторов окажутся равными (+1), а нижнего – (-1).

Матрицы двух- и трехфакторного экспериментов будут выглядеть так (рис.6.2а, б).

Число опытов (и соответственно строк) определится уравнением N=2m, где m – число факторов.

В столбцах х1 чередуют значения +1; (-1).

Во втором знаки меняют через 2 номера, затем через 4, 8, 16, 32, 64, 128 и т.д.

Поскольку информацию об уровне каждого фактора несет только знак перед единицей (рис.6.2а), то единицу в матрице не пишут, а оставляют лишь ее знак (рис.6.2б). В крайнем правом столбце записывают результат опыта уi.

Например: в первом опыте трехфакторного эксперимента (рис.6.2б) первый фактор х1 берут на верхнем уровне, второй и третий – на нижнем. По окончании такого опыта результат записывают в виде уi.

Матрица ПФЭ не только решает задачу поиска всех возможных сочетаний уровней и факторов, но может существенно упростить задачу определения коэффициентов уравнения регрессии. Для этого следует обратить внимание на свойства матрицы планирования эксперимента.

1.Симметричность матрицы состоит в том, что сумма элементов любого вектор-столбца для каждого фактора равна нулю.

188

2.Свойство нормированности заключается в том, что сумма квадратов

элементов любого вектор-столбца для каждого фактора равна числу опытов (поскольку (+1)2=1 и (-1)2=1).

3.Ортогональность матрицы заключается в том, что сумма произве-

дений соответствующих элементов двух вектор-столбцов (например,

x1 x2 , или x1 x3 , или x2 x3 ), равна нулю.

4.Рототабельность матрицы ПФЭ выражает тот факт, что дисперсии

предсказанных значений отклика на равных расстояниях от центра плана постоянны и минимальны.

а)

Рис. 6.2. Матрицы планирования двух и трехфакторного эксперимента

Определение коэффициентов уравнения регрессии на основе опытных данных

В уравнении три неизвестных коэффициента: b0; b1; b2.

Опыты проведены в четырех точках (матрица рис.6.2а), но зафиксированные в них значения у1, у2. у3 и у4 определены лишь с некоторым приближением, доступным для условий эксперимента.

В этом случае левая часть уравнения (6.6) – найденная в опыте, и правая– расчетная могут несколько отличаться друг от друга, т.е. будет иметь место лишь приближенное равенство:

189

где xji – значения фактора j в i-том (по строке) опыте.

Если учесть, что разница между левой и правой частями уравнений системы (6.6) невелика и равна ошибке опыта ε, то ее можно представить в виде:

В курсе теории вероятностей доказывается, что наиболее вероятными значениями коэффициентов будут те из них, которые снизят до минимума сумму квадратов отклонений εi (или остатков, как их иногда называют). Из этого следует и название используемого метода – метод наименьших квад-

ратов.

Сумма квадратов отклонений будет равна:

i 1

Для того чтобы функцию нескольких переменных (в данном случае b0, b1, b2) привести к минимальному значению, нужно взять частные производные по этим переменным и приравнять их к нулю, а затем решить систему полученных уравнений:

Учитывая, что если удвоенная сумма равна нулю, то нулю равняется и сама сумма, и то обстоятельство, что искомые значения коэффициентов уравнения регрессии справедливы для всех уравнений системы, можно получить:

190