
892
.pdfОкончательно основная теория теоремы подобия, так называемая П- теорема, о возможности выражения физических законов в виде зависимости между безразмерными числами (критериями подобия) была доказана в начале ХХ столетия и опубликована в трудах Кучинского аэродинамического института, организованного Н.Е. Жуковским и работающего под его руководством в 1912 г.
П-теорема формулируется следующим образом.
Функциональная зависимость между характеризующими процесс величинами может быть представлена в виде зависимости между составленными из них критериями подобия.
Иными словами, П-теорема содержит доказательство возможности приведения того или иного уравнения к критериальному виду.
Третья теорема (теорема Кирпичева-Гухмана) ограничивает пределы распространения понятия явлений подобия и кратко формулируется: по-
добными явлениями будут те, которые имеют подобные условия однозначности и одинаковые определяющие критерии.
Под условием однозначности понимают геометрическое подобие, т.е. пропорциональность линейных размеров и равенство угловых параметров, установление значений физических параметров, формирование начальных и граничных условий.
Итак, в соответствии с идеями Ж. Фурье и основной П-теоремой теории подобия, критериальные уравнения могут быть составлены на основе анализа размерностей.
5.2.2. Анализ размерностей в теории подобия
Очень часто с помощью теории размерностей можно найти искомую закономерность связи между физическими величинами, когда нахождение ее прямым путем встречает значительные математические трудности, либо требует знания таких деталей процесса, которые заранее неизвестны.
Единицы физических величин, подобранные определенным образом, составляют систему единиц – т.е. совокупность единиц физических величин, образованную с принятыми правилами. Существует большое количество систем единиц: СГС, МКГС, СИ и др. В настоящее время используют в основном систему СИ, основные единицы которой представлены в таблице 5.3. Помимо обозначения величин в ней приведены обозначения размерностей. Поскольку таких обозначений может быть много, то для определенности используют чаще встречаемые, представленные, например, во вполне доступном учебном пособии А.В. Филончикова [18].
Все производные единицы СИ получены на основе физических зако-
нов. Допустим, единица силы Ньютон определяется из закона Ньютона
F m a ,
как произведение массы на ускорение, т.е.
1Н кг м / с2 .
71
Таблица 5.3
Основные единицы физических величин
Наимено- |
Дли- |
Масса, |
Вре- |
Сила |
Темпера- |
Количе- |
Сила |
|
вание ве- |
мя, |
тока, |
ство ве- |
света, |
||||
на, |
кило- |
тура, |
||||||
личин и |
се- |
ам- |
щества, |
канде- |
||||
метр |
грамм |
Кельвин |
||||||
единиц |
кунда |
пер |
моль |
ла |
||||
|
|
|
||||||
Обозначе- |
|
|
|
|
|
|
|
|
ния вели- |
м |
кг |
с |
А |
К |
моль |
кд |
|
чин |
|
|
|
|
|
|
|
|
Обозначе- |
|
|
|
|
|
|
|
|
ния раз- |
L |
М |
T |
I |
Т |
|
i |
|
мерностей |
|
|
|
|
|
|
|
Единица работы (Джоуль) определится как произведение силы на перемещение, т.е.
1Дж Н м кг м2 / с2 ,
единица скорости м/с и т.д.
Но, вообще говоря, скорость может быть обозначена и иначе, например, в км/ч.
Для того, чтобы не вникать в соотношение кратных единиц в теории размерностей вводят их обозначения. Размерность скорости обозначают как
L|T, единицу площади м2 представляют как L2, единицу плотности – как
М/L3.
Для характеристики изменения производной единицы в зависимости от изменения основных единиц служит формула размерности, т.е. математическое выражение, показывающее, во сколько раз изменится производная единица при определенных изменениях основных единиц.
Формула размерности формируется как некоторая степенная зависимость.
Если, например, некоторая величина А имеет формулу размерности
А LP M qT r ,
то при изменении длины она изменится пропорционально степени Р, при изменении единицы массы – пропорционально степени q, а при изменении времени – пропорционально r.
Определение этих показателей степеней, если это возможно, и составляет решение задачи.
Например, автомобиль массой m, опирается на пружинные подвески
(рис.5.6).
В положении равновесия он занимает положение А. Под воздействием внешних сил (допустим, со стороны дороги) пружины сожмутся на величину l. В простейшей модели движение рассматривается только вдоль вертикали, т.е. с единственной пока степенью свободы и одинаковыми пружинами. Пусть их общая жесткость равняется С.
72
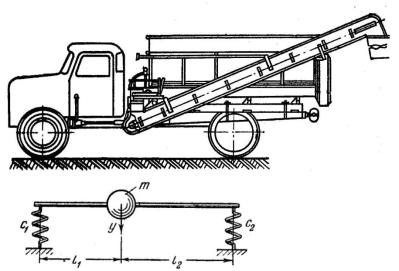
Рис. 5.6. Модель колебания автомобиля
В следующих разделах будут рассмотрены и более сложные случаи плоских и пространственных колебаний.
Для восстановления уровня автомобиля в исходное положение к нему необходимо приложить силу, пропорциональную l, т.е. F=C l.
Время восстановления пружины желательно установить, так как от этой величины зависит частотная характеристика динамической системы подвески автомобиля.
Можно предположить, что это время t будет зависеть от l, m, c, т.е. t = f (l, m, c) .
Размерность величин, входящих в формулу, соответственно: L – для величины деформации l, М – для массы m и МТ2 – для коэффициента с.
Алгебраической функции t kl pmqcr ,
где k – неизвестный безразмерный коэффициент пропорциональности; будет соответствовать формуле размерности:
T Lp M q M T 2 r Lp M q rT 2r . |
(5.1) |
Анализ частей уравнения показывает, что в левой части есть только Т с показателем степени равным единице. M и L там отсутствуют, но их мож-
но ввести туда в нулевой (0) степени, тогда |
|
L0 M 0T1 Lp M q rT 2r . |
(5.2) |
Поскольку размерность левой и правой частей должны быть одинаковыми, то из показателей степеней можно составить три уравнения с тремя неизвестными (p, q, r).
Первое уравнение системы – это сумма показателей степени при L в левой и правой частях формулы равномерностей, второе – сумма показателей степени при М, а третье уравнение – сумма показателей степени при Т.
p 0 |
|
q r 0 |
|
. |
2 r 1
73

Чтобы не перепутать, к какой размерности относятся те или иные показатели степени, запись системы уравнений осуществляют так:
L : p 0 |
|
|
|
M : q r 0 . |
|
T : 2 r 1 |
|
|
|
Решение этой системы дает r = -1|2; q = 1|2 и позволяет искомую зависимость (5.1) привести к уравнению:
T = k l0m1|2k-1\2, |
т.е. t k |
|
m |
|
. |
|
|||||
|
|
|
c |
||
Уравнение дает общую закономерность, т.к. не определен пока коэффициент с. Но есть уже и нетревиальный результат: оказалось, что время возвращения в исходное состояние не зависит от удлинения пружины.
Точное решение может быть определено экспериментально или исходя из законов механики:
t |
|
|
m |
|
. |
|
|
|
|||
|
2 |
|
c |
||
К сожалению, столь простой способ определения показателей степени исходного уравнения не всегда возможен. Часто это связано с тем, что в него входит большое число факторов, во всяком случае больше независимых размерностей. В этом случае часть уравнений системы оказывается зависимой.
В этом случае к формуле размерностей добавляют (согласно П- теореме) критериальное уравнение, например:
П1 f (П2 П3П7...Пm ) , |
(5.3) |
где Пi – критерии подобия тех или иных показателей (факторов или соответствующих размерностей), которые приходится предварительно находить.
Критерием того, что то или иное сочетание факторов или размерностей могут представить коэффициент подобия, является его безразмерность. Примером разработки критериального уравнения с использованием теории размерностей может быть исследование характеристик подобия вентиляторов. Рабочий процесс вентилятора определяют следующие величины: плотность среды ρ, кг/м3, число оборотов в единицу времени n, с-1, диаметр крылача D, м, расход воздуха Q, м3/с, напор Н, н/м2 и мощность N, вт.
Между этими величинами существует некоторая функциональная зависимость:
f(ρ, n, D, Q, H, N) = 0,
которая, согласно П-теореме, может быть представлена в виде зависимости между критериями подобия. Подобными вентиляторами считаются те, у которых все угловые параметры одинаковы, а линейные – пропорциональны.
Для перехода к критериям подобия в качестве основных единиц могут быть выбраны ρ, n, D. Размерности остальных величин в новых
74
единицах окажутся следующими: |
|
|
|
|
|
|
|
|
|
|
|
||||
Q D n ; |
H D 2 n 2 ; |
N D 5 n 3 . |
(5.4) |
||||||||||||
Применяя метод нулевых размерностей находят: |
|
||||||||||||||
|
|
Q |
|
H |
|
|
|
N |
|
|
|
|
|
|
|
f 1,1,1, |
|
|
, |
|
|
|
, |
|
|
|
|
0 |
, |
(5.5) |
|
3 |
|
2 |
|
2 |
5 |
|
3 |
||||||||
|
|
n |
|
n |
|
n |
|
|
|
|
|||||
|
|
D |
|
D |
|
|
D |
|
|
|
|
|
|||
|
|
|
|
|
|
или Ф[П1; П2; П3] = 0, |
(5.6) |
|||||
где П |
Q |
; П |
|
|
H |
|
; П |
|
|
N |
. |
|
|
2 |
|
|
3 |
|
|
||||||
1 |
D3n |
|
D2n2 |
|
|
D5n3 |
|
|||||
|
|
|
|
|
|
|
||||||
На основании экспериментальных исследований нетрудно построить на плоскости обобщенную характеристику вентилятора П1=f(П2) с параметром П3. Каждая точка плоскости будет при этом соответствовать шести параметрам, что в конечном итоге обеспечивает принципиальную возможность нахождения всех показателей степеней параметров степенного комплекса.
Соотношения (5.4, 5.5, 5.6) используют для расчета вентиляторов методом подобия и построения универсальных характеристик.
В этом случае выбирают вентилятор-образец с параметрами, допустим, Q, HT, D, b, n и пересчитывают его размеры и режим работы так, чтобы он обеспечивал необходимый расход Qx и напор HTx.
Из коэффициентов подобия следует, что
Q |
X |
|
n D3 |
|
n |
|
|
Qx D3 |
|
|
x х |
, откуда |
|
x |
|
(5.7) |
|||
|
|
nD3 |
|
|
QD3 |
||||
Q |
|
n |
|
||||||
|
|
|
|
|
|
|
|
х |
|
Н |
Тx |
|
n2 D2 |
|
n2 |
|
HTx D2 |
|
|
||
|
x x |
, откуда |
x |
|
|
. |
(5.8) |
||||
Н |
|
n2 D2 |
n2 |
H |
D2 |
||||||
Т |
|
|
|
|
|||||||
|
|
|
|
|
|
|
T х |
|
|
||
Если первое из этих соотношений возвести в квадрат, то из равенства левых частей уравнений следует равенство правых, т.е.
Qx2 D6 |
|
НТx D2 |
|
Q2 |
|
D4 |
|
Н |
|
|
|
||
|
|
|
|
или после сокращений |
x |
|
|
|
Тx |
, |
|||
Q2 D6 |
|
|
D2 |
Q2 |
|
D4 |
|
|
|||||
|
Н |
Т |
|
|
|
Н |
Т |
||||||
x |
|
|
х |
|
|
|
х |
|
|
|
|||
откуда можно определить наружный диаметр проектируемого вентилятора:
D 4 |
Qx2 |
|
HT |
D4 D 4 |
Qx2 |
|
HT |
. |
|
|
|
|
|
|
|
||||
x |
Q2 |
|
HT |
|
|
Q2 |
|
HTx |
|
|
|
X |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
Теоретический напор НТ = h/η,
где h – действительный напор, развиваемый вентилятором, а η – коэффициент полезного действия.
С учетом этого
|
Q2 |
h |
|
|
D D 4 |
x |
|
|
. |
|
|
|||
х |
Q2 |
h |
|
|
|
|
|||
|
|
|
x |
|
После этого по уравнению (5.12) следует найти nx
75
|
|
Q D3 |
|
|
||
nx |
n |
x |
|
|
|
|
Q |
D3 |
|
|
|||
|
|
|
|
|||
|
|
|
х |
|
|
|
и коэффициент геометрического подобия k |
Dx |
, с помощью которого |
||||
D |
||||||
находят все недостающие параметры проектируемого вентилятора.
5.3. Аналоговое моделирование
Возможность создания аналоговых моделей опирается на сходство описания в ряде случаев явлений, различных по своей физической сущности. Примерами могут служить даже основательные законы механики, физики и химии.
В механике широко используется закон о том, что «Изменение кинетической энергии Т m 2 / 2
приложенных к нему».
Применительно, допустим, к некоторой силе сопротивления FT, препятствующей движению тела вдоль оси х, закон выражается уравнением:
FT dT dx .
dx .
В одном из разделов физики изучаются явления, связанные с переносом тепла и тепловыми потоками. Тепловой поток qT в направлении х связан с изменением температуры Т в этом направлении и описывается законом Фурье:
qT dTdx ,
где λ – коэффициент теплопроводности.
В разделе «Электричество» изучается закон Ома в дифференциальной форме, который связывает перенос количества электричества в единицу времени (ток i) через проводник, имеющий погонное сопротивление , с изменением величины падения напряжения U по длине проводника х:
i 1 du .dx
В физической химии одним из основных законов является закон Фика, связывающий перенос количества вещества (поток вещества gВ) в некотором направлении х и с изменением концентрации С вещества в этом направлении.
gВ D dCdx ,
где D – некоторая постоянная.
Во всех этих физических законах легко замечается одна форма математических выражений, тогда как физическая сущность различна.
Такие одинаковые по форме явления называют изоморфными. Они отличаются только материальным, физическим содержанием входящих в их описания символов.
76
Математический изоморфазм различных физических систем позволяет одни системы представлять с помощью других
Целесообразность таких замен может диктоваться целым рядом обстоятельств, таких, например, как простота и относительная дешевизна модели, удобство постановки различных экспериментов, наличие необходимой аппаратуры, соображениями техники безопасности и т.д.
На этом принципе математического изоморфизма основано аналоговое моделирование. Оно может быть в виде специального устройства, так называемого модель-аналога или осуществлено на аналоговой вычислительной машине (АВМ).
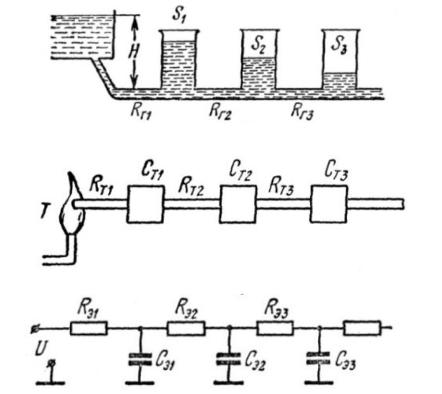
Например, процесс потери напора воды в сложной и громоздкой водопроводной или оросительной системе можно изучить на моделях передачи тепла или на электрической схеме (рис. 5.7). Сопоставление этих моделей показывает, что аналогом гидравлического напора Н при теплопередаче может быть температура Т, а в электрической – напряжение U. Аналогами гидравлического сопротивления могут быть, соответственно, тепловые или электрические сопротивления.
Аналогом напора – являются теплоемкости СТ и емкости конденсаторов Сi.
а)
Рис. 5.7.
Схемы моде- лей-аналогов
б)
с)
Прямыми аналогами механической, допустим, демпферной системе (рис. 5.8а) могут быть электрические схемы, содержащие резисторы R, индуктивности L и емкости С (рис. 5.8б, 5.8в).
77
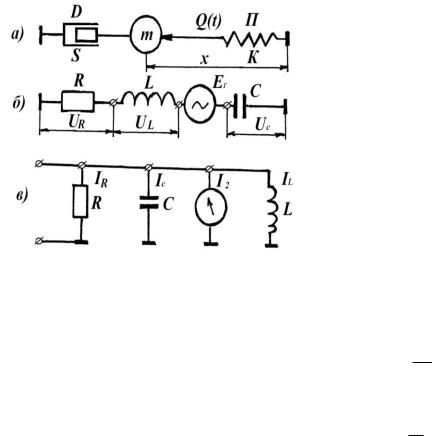
Рис. 5.8. Аналоги механической системы
Элементами механической системы являются масса m, совершающая продольные колебания, пружина П с коэффициентом жесткости К, демпфер Д с коэффициентом трения S и внешняя сила Q(t).
Аналогом скорости V системы можно считать ток I, силы инерции
Q(m) – падение напряжения от индуктивности U L L dIdt . Аналогом силы трения – падение напряжения на сопротивление UR RI и аналогом вос-
станавливающей силы – напряжение на емкости UC C1 Idt .
Аналогом внешней силы Q(t) будут электродвижущая сила генерато-
ра EГ(t).
Иными словами индуктивность L аналогична массе m, сопротивление R – коэффициенту трения S и емкость С – коэффициенту податливости пружины 1/k.
Наиболее распространенные аналоги механических и электрических систем представлены в табл. 5.3, а возможные варианты полей-аналогов – в
табл. 5.4.
При моделировании тепловых систем фазовыми переменными типа потока являются температуры Т, а типа потенциала – тепловые потока Ф.
Значение переменной типа потенциала Ф и характеризует величину теплового потока, затрачиваемую на изменение кинетической энергии дискретного элемента твердого тела в процессе теплоередачи, а значение Фд – величину потерь, обусловленную преодолением теплового сопртивления.
Упругими свойствами тепловая система не обладает. Это следует из того, что тепловая энергия может передаваться только от более нагретых элементов к менее нагретым.
В качестве нагрузочного элемента при моделировании тепловыи и аэродинамических процессов часто используют электропроводную бумагу, позволяющую исследовать пространственные характеристики полей, путем измерения потенциалов в их различных точках.
78
Таблица 5.3 Часто используемые аналоги механических и электрических систем
Механическая система |
|
|
|
|
|
|
Электрическая система |
|
|
|
|
|
|
|
|||||||||||||
Физическая ве- |
Линейное пе- |
Угловое переме- |
|
Физическая величина |
|
|
|
|
|
|
|
||||||||||||||||
личина |
ремещение |
щение |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Обобщенная ко- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Магнитное по- |
|
|
|
|
|
|
|
|
|
х |
|
|
|
|
θ |
Заряд |
|
q |
|
|
|
токо- |
|
|
|
Ψ |
|||||||||
ордината |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сцепление |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обобщенная |
|
|
V |
|
|
|
|
Ω |
Ток |
|
I |
|
|
|
Напряжение |
|
|
|
U |
||||||||
скорость |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обобщенная си- |
|
|
Q |
|
|
|
|
М |
Напряжение |
|
U |
|
|
|
Ток |
|
|
|
|
I |
|
||||||
ла |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обобщенная |
|
|
M |
|
|
|
|
θ |
Индуктивность |
|
L |
|
|
|
Емкость |
|
|
|
C |
|
|||||||
масса |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Виртуальная |
|
Q d x |
|
M d θ |
|
U t d |
|
|
I d ψ |
||||||||||||||||||
работа |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Количество |
|
m V |
|
|
Q Ω |
Магнитное по- |
|
Ψ |
|
|
|
Заряд |
|
|
|
q |
|
||||||||||
движения |
|
|
|
токосцепление |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Коэффициент |
|
|
Sл |
|
|
|
|
Sк |
Сопротивление |
|
R |
|
|
|
Проводимость |
|
|
|
G |
||||||||
трения |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Податливость |
ел |
1 |
|
еR |
|
|
1 |
|
Емкость |
|
C |
|
|
|
Индуктивность |
|
|
|
L |
|
|||||||
К л |
К R |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Жесткость |
|
|
Кл |
|
|
|
КR |
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
L |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Кинетическая |
T |
1 |
mV 2 |
T |
1 |
2 |
Магнитная энер- |
WM |
1 L / 2 |
Электрическая |
WЭ |
|
1 |
CU 2 |
|||||||||||||
энергия |
|
2 |
|
|
|
|
|
2 |
|
|
|
гия |
|
|
|
|
|
|
энергия |
|
|
2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||
Потенциальная |
|
|
|
|
|
|
|
|
|
|
|
|
Электрическая |
WЭ |
1 |
|
q2 |
Магнитная |
WM |
1 |
|
2 |
|||||
энергия |
|
|
|
|
|
|
|
|
|
|
|
|
энергия |
|
|
|
|
|
энергия |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
C |
|
|
|
2 |
|
L |
|||||
Рассеяние энер- |
F |
1 |
SлV 2 |
F |
1 |
SR 2 |
Рассеяние энер- |
WP |
1 |
RI 2 |
Рассеяние |
|
|
|
|
|
|
|
|||||||||
гии |
|
2 |
|
|
|
2 |
|
|
|
|
гии |
|
2 |
|
|
|
|
энергии |
|
|
|
|
|
|
|
||
79
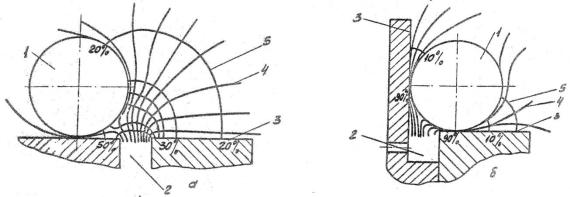
Таблица 5.4
Возможные варианты выбора аналогов при исследовании полей
Постоянное |
Стационарное |
|
|
|
|
|
Потенциальное |
||||||||
электрическое |
электрическое |
Постоянное |
гидродинамическое |
||||||||||||
поле в диэлек- |
поле тока в про- |
магнитное поле |
поле идеальной |
||||||||||||
|
|
трике |
водящей среде |
|
|
|
|
|
|
жидкости |
|||||
E=gradU |
E=-gradU |
H=-gradUM |
|
V=-gradθ |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
ds GM |
|||
Dds Q |
|
ds I |
Bds Ф |
|
V |
||||||||||
s |
|
|
|
s |
|
s |
|
|
|
|
s |
|
|
||
|
div D=0 |
|
div δ=0 |
|
div B=0 |
|
|
div V=0 |
|||||||
|
rot E=0 |
|
rot E=0 |
|
rot H=0 |
|
|
rot V=0 |
|||||||
U - |
|
электриче- |
U – |
|
электриче- |
UM – скалярный |
θ – гидродинамиче- |
||||||||
ский потенциал; |
ский потенциал; |
магнитный |
по- |
ский |
|
потенциал |
|||||||||
E |
- |
вектор |
E |
– |
вектор |
тенциал; |
|
скорости; |
|||||||
напряженности |
напряженности |
H |
|
– вектор |
V – вектор скоро- |
||||||||||
электрического |
электрического |
напряженности |
сти; |
|
|
||||||||||
поля; |
|
поля; |
|
магнитного |
по- |
ρ – плотность; |
|||||||||
D - |
|
электриче- |
δ - вектор плот- |
ля; |
|
|
|
|
GM – расход массы |
||||||
ское смещение; |
ности тока; |
B – |
|
магнитная |
|
|
|
||||||||
Q - поток элек- |
I - ток |
|
индукция; |
|
|
|
|
||||||||
трического |
|
|
|
|
Ф – |
|
магнитный |
|
|
|
|||||
смещения; |
|
|
|
|
поток; |
|
|
|
|
||||||
В качестве примера использования таких аналогов в исследованиях, связанных с земледельческой механикой, можно провести работу А.Е. Петренко [20] из Украинской СХА, где с помощью электропроводной бумаги было изучено аэродинамическое поле в щелевых высевающих аппаратах
(рис.5.9).
Рис. 5.9. К моделированию воздушного поля щелей с одной направляющей плоскостью (а) и двумя направляющими плоскостями (б): 1 - семя; 2 – вакуумная щель; 3 – направляющая плоскость; 4 – линии тока; 5– эквипотенциалы (от 10 до 90%), т.е. линии равных скоростей, выраженных в % от скорости воздуха в плоскости щели
80
