
892
.pdf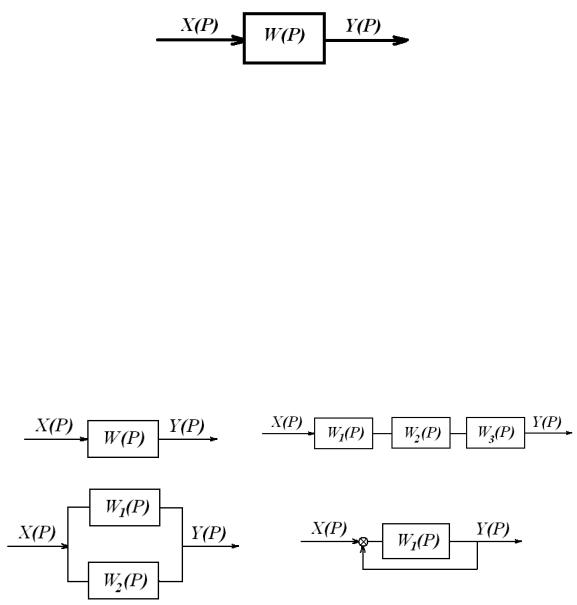
где у = ∆ψ; х = f(t).
В преобразованиях Лапласа уравнение может быть представлено как
Т12 P2 Y (P) T2 P Y (P) Y (P) kX(P) .
Передаточная функция этого динамического звена будет равна:
W (P) |
|
k |
|
|
|
|
. |
(5.29) |
|
T 2 P2 |
T P 1 |
|||
1 |
2 |
|
|
|
Свойства динамического звена могут в этом случае быть представлены в виде схемы:
Рис.5.25. Схема функционирования динамического звена в комплексной области (P = α + i ω)
Свойства передаточной функции
Передаточные функции обладают рядом свойств, позволяющих существенно облегчить анализ сложных динамических систем.
Если система состоит из отдельных узлов и элементов с различными связями, то при определении передаточной функции всей системы возникает необходимость преобразования многозвенной системы с целью ее упрощения или замены одним сложным звеном. Такие преобразования выполняют обычно с помощью структурных схем.
Структурная схема динамической системы представляет собой графическое изображение системы в виде совокупности динамических звеньев с обозначением их передаточных функций и изображений входных и выходных переменных (рис. 5.26).
а) элементарное звено |
б) последовательно соединенные звенья |
в) параллельно соединенные |
г) звено, охваченное обратной связью |
звенья |
|
Рис. 5.26. Структурная схема возможного соединения элементарных динамических звеньев
111
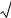
Свойства передаточных функций можно сформулировать следующим образом.
1.Если динамическая система может быть представлена в виде последовательно соединенных звеньев, то передаточная функция системы равна произведению передаточных функций отдельных звеньев:
n
W(P) W1(P) W2 (P) ...Wn (P) Wi (P) .
i1
2.При параллельном соединении звеньев их передаточные функции алгебраически складываются:
n
W(P) W1(P) W2 (P) ...Wn (P) Wi (P) .
i1
3.При наличии обратной связи передаточную функцию системы нахо-
дят по уравнению W (P) |
W1(P) |
, причем знак «+» используется |
1 W (P) |
||
|
1 |
|
при отрицательной, а «–» – при положительной обратной связи. Составление структурной схемы и определение общей передаточной
функции позволяет не только упростить процесс решения систем дифференциальных уравнений, но и способствует получению оценок динамических свойств исследуемых объектов. Так, заменяя в выражении передаточной функции переменную Р на (iω), находят частотную характеристику системы.
Для примера с сошниковой группой это будет
W i |
|
|
k |
|
|
. |
(5.30) |
|
|
|
|
|
|||
T 2 |
i 2 |
Т |
2 |
i 1 |
|||
1 |
|
|
|
|
|
||
С математической точки зрения, частотная характеристика представляет собой комплексную функцию. Четные степени величины (iω), содержащие i2 = -1, i4 = 1 и т.д. равны ±ω, а нечетные, содержащие мнимую еди-
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ницу i |
|
1 , равны ±(iω), поэтому после разделения комплексной функ- |
|||||||||||||||||
ции на действительную и мнимую части можно получить: |
|
|
|
|
|||||||||||||||
|
|
|
|
|
W(iω) = U(ω) + iV(ω) . |
|
|
|
|
(5.31) |
|||||||||
Так, если умножить и разделить правую часть уравнения (5.30) на |
|||||||||||||||||||
1 Т 2 2 |
iT , можно получить: |
|
|
|
|
|
|
|
|
||||||||||
1 |
2 |
|
k (1 T 2 |
2 ) iT |
|
k 1 T 2 iT |
|||||||||||||
|
|
|
|
|
|
||||||||||||||
W (i ) 1 T12 2 iT2 |
1 T12 2 iT2 |
1 T |
2 2 2 |
T 2 |
|||||||||||||||
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
1 |
2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
||
или |
1 T |
2 2 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
k |
kT |
|
|
|
|
|
||||||||
|
|
W (i ) |
|
1 |
|
i |
|
|
|
|
2 |
|
|
. |
|
|
|||
|
|
1 T 2 2 T 2 |
1 T 2 2 |
T 2 |
|
||||||||||||||
|
1 |
2 |
|
|
|
1 |
|
|
2 |
|
|
|
|
||||||
В полученном выражении |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
k 1 T |
2 2 |
|
, а V ( ) |
|
|
|
kT |
|
|
|
|
||||
|
1 |
|
|
|
|
|
2 |
|
|
|
|
||||||||
U ( ) |
|
|
|
|
|
; |
|||||||||||||
1 T 2 2 2 |
(T )2 |
1 T |
2 2 |
2 (T )2 |
|||||||||||||||
|
1 |
|
2 |
|
|
|
|
|
1 |
|
2 |
|
|
||||||
112
Известно, что любое комплексное число может быть представлено в виде вектора в координатах U(ω) и V(ω).
Абсолютное значение или модуль А(ω) частотной характеристики определяется как геометрическая сумма U(ω) и V(ω), а угол (ω) наклона вектора к оси U(ω)
arctg V ( ) .U ( )
Рис. 5.27. Числовые характеристики частотной функции А(ω) и (ω)
при фиксированном значении ω
При изменении ω в широких пределах вектор А(ω) будет изменять величину и одновременно поворачиваться, изменяя наклон луча, соединяющего начало координат комплексной плоскости и данную точку кривой, описываемой концом вектора А(ω).
Такая кривая представляет собой амплитудно-фазовую частотную характеристику системы.
С точки зрения физики и механики, частотная характеристика отражает реакцию системы на внешние воздействия в виде гармонических коле-
баний.
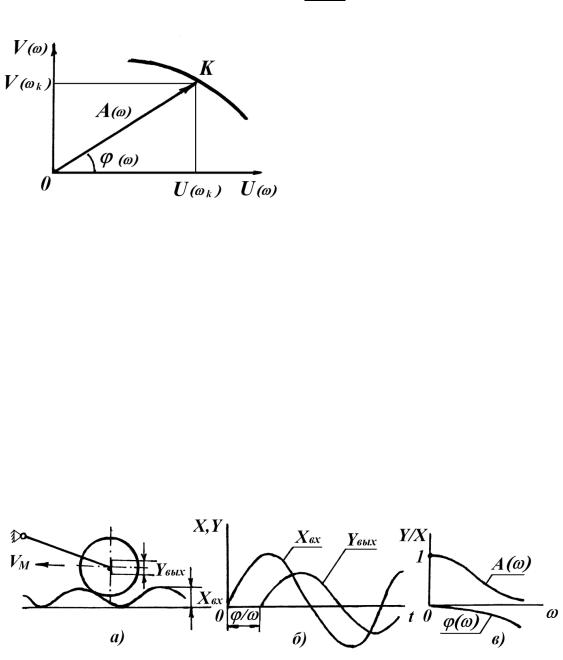
Представим себе движение сошника сеялки по поверхности поля, имеющего неровности в виде, например, синусоиды (рис. 5.28а). Если амплитуду колебаний неровностей обозначить Х, а колебаний У, то их соотношение будет изменяться при различных скоростях VМ и соответствующих частот ω.
Рис.5.28. Схема, характеризующая реакцию динамической системы внешних воздействий в виде гармонических колебаний
Если скорость VМ ничтожно мала, то очевидно сошник повторит колебания профиля поверхности поля, т.е. совершит колебания с той же частотой ω и амплитудой Увых = Хвх.
В случае увеличения скорости сошник не будет успевать копировать
113

поверхность, и его движение будет представлять синусоиду той же частоты но с меньшей амплитудой и сдвинутой по фазе (рис.5.29б), а при некоторой скорости (VМ) (если продолжить мысленный эксперимент) перестанет реагировать на внешние возмущения (рис.5.29в) (известный афоризм шоферов «больше скорость – меньше ям»).
Сдвиг фаз θ в этом случае будет увеличиваться.
При анализе и синтезе динамических систем используются и операторы других видов, определяющие свойства этих систем при воздействиях различного типа.
Важным оператором динамической системы является импульсная характеристика h(t), определяющая реакцию системы на так называемую дельта-функцию (t) (единичная импульсная функция), причем,
0 |
при t 0 |
|
|
t dt 1 . |
|
|
|||
t |
|
, |
|
|
при t 0 |
|
|
||
|
|
|
|
|
Если единичный импульс подается в момент t = t0 (рис.5.29), то его записывают в виде:
t t0 |
0 |
при t t |
|
|
|
0 . |
|
|
при t t |
0 |
|
|
|
|
|
Рис. 5.29. Типовые входные воздействия
Эти выражения определяют математическую модель идеализированного импульса, длительность которого равна нулю, а уровень – бесконечности. При уровне, равном единице, импульсное воздействие конечной длительности η будет иметь вид:
|
t t |
|
|
0 при (t0 |
) t t0 |
|
|
|
|
t t |
|
dt . |
|||
|
|
; |
|
|
|
|
|||||||||
|
|
0 |
|
1 при t |
0 |
t (t |
0 |
) |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Зависимость между воздействием f(t) и реакцией на него y(t) может быть представлена интегральным уравнением:
t
y(t) f (t )h( )d .
0
Между импульсной характеристикой h(t) и передаточной функцией W(P) существует связь, определяемая преобразованием Лапласа,
114
W (P) L h(t) h(t)е Ptdt .
0
С характеристикой h(t) связана и переходная характеристика системы Yn(t), определяющая переходный процесс на выходе системы. Переходная характеристика является реакцией системы на воздействие f(t) = 1(t) в виде скачка, равного по величине единице (рис.5.29в). Практически единичный скачок означает мгновенное и резкое изменение входного воздей-
ствия, причем, δ(t )= d[1(t)]/dt.
Связь между импульсной и переходной характеристиками выражается равенством:
h(t) = d[yn(t)]/dt.
Таким образом, для линейных динамических систем основными операторами, определяющими соответствующее преобразование входных воздействий, являются передаточные функции, частотные, импульсные и переходные характеристики. Они являются наиболее полными динамическими характеристиками системы, определяющими ее свойства в области комплексной переменной, частотной и временной областях.
Если обратить внимание на то, что в основе всех характеристик находятся дифференциальные уравнения движения тел, в свою очередь являющиеся тем или иным выражением законов физики, таких как законы сохранения массы и энергии, то становится, во всяком случае, объяснимым, что самые разнообразные процессы могут иметь совершенно схожие модели и их характеристики. Это дало возможность унифицировать отдельные системы по их динамическим свойствам и свести их к так называемым типовым звеньям.
Такой подход облегчает анализ динамических свойств систем. Наиболее часто в исследованиях используются такие типовые звенья,
как
-безинерционное;
-апериодическое (инерционное);
-колебательное;
-дифференцирующее;
-интегрирующее;
-звено с запаздыванием.
Безинерционное звено (то же самое пропорциональное, идеальное, усилительное) при переходном процессе постоянно сохраняет пропорциональную зависимость между отклонениями входной и выходной координаты.
Связь между входом и выходом такого звена выглядит в виде алгебраического уравнения:
y = k x,
где k – коэффициент усиления.
Передаточная функция, частотная и переходная характеристики определяются выражениями W(P) = k; W(iω) = k; yp(t) = k.
115
Примерами такого звена могут быть рычажные соединения, механические редукторы, электронные усилители и т.п.
Апериодические (инерционные) звенья могут иметь первый или второй порядок.
У апериодического звена первого порядка дифференциальное уравнение имеет вид:
T dydt y kx ,
где Т – постоянная времени, k – коэффициент усиления. Передаточная и частотная функции соответственно равны:
W (P) |
k |
|
W (i ) |
k |
|
|
; |
|
. |
||
TP 1 |
T (i ) 1 |
||||
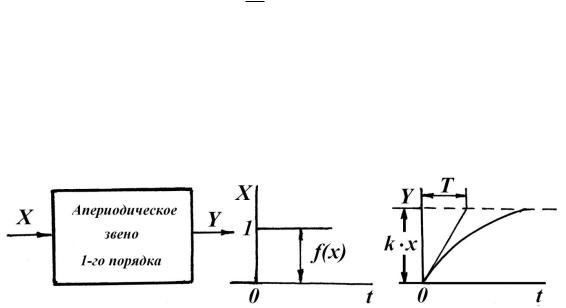
Переходная характеристика представляется в виде экспоненты (рис.
5.30).
Рис. 5.30. Переходная характеристика апериодического звена первого порядка
Примеры таких звеньев:
1.Тракторный дизель. Если скачкообразно изменить подачу топлива, то обороты плавно изменятся до нового значения.
2.Электродвигатель. При изменении напряжения плавно изменяется температура.
3.Зерноуборочный комбайн с системой автоматического регулирова-
ния подачи хлебной массы.
Апериодическое второго порядка и колебательное звенья описываются одинаковыми дифференциальными уравнениями:
|
T 2 |
y T y |
y kx, |
|||
1 |
2 |
|
|
|
||
передаточными и частотными функциями: |
||||||
W (P) |
k |
|
|
W i |
k |
|
|
; |
|
. |
|||
T12 p2 T p 1 |
T12 i 2 T2 i 1 |
|||||
Различаются они лишь соотношениями коэффициентов Т1 и Т2 и видом переходных характеристик.
У апериодического звена второго порядка Т2 ≥ 2Т. Это вызвано тем, что силы вязкого трения превышают инерционные. Из-за большого поглощения энергии при трении колебания в системе не возникают (рис. 5.31).
116
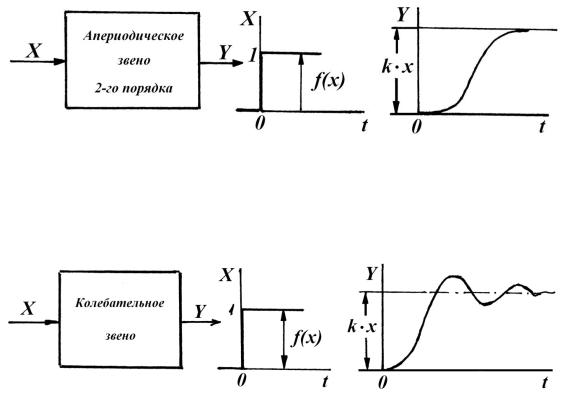
Рис. 5.31. Переходная характеристика апериодического звена второго порядка
У колебательного звена Т2 < 2Т, а переход с одного уровня на другой сопровождается дополнительными колебаниями (рис. 5.32).
Рис. 5.32. Переходная характеристика колебательного звена
Параметры сошниковой группы желательно подобрать так, чтобы звено было апериодическим, и после встречи с неровностями не возникали дополнительные колебания.
До сих пор содержание математических моделей, в том числе и в виде «вход» и «выход» (рис. 5.25), определялось достаточно сложно, на основе составления и решением систем дифференциальных уравнений. В принципе возможен и другой путь решения, основанный на анализе соотношений информации о входных и выходных параметрах. В таком виде модели причисляют к так называемым информационным моделям.
Методы их составления и анализа будут рассмотрены в следующих главах.
5.5.4. Математические модели, основанные на использовании уравнения П. Аппеля
Удачным примером анализа технологических процессов с использованием уравнения П. Аппеля является исследование движения хлебной массы в зазоре между молотильным барабаном и декой, выполненное проф. Э.И. Липковичем [35]. Дело в том, что при разработке модели обмолота хлебной массы В.П. Горячкин использовал теорию неупругого удара, которая содержит предположение о том, что после соударения барабана с хлебной массой ворох приобретает скорость бича. Наблюдения за работой молотильного аппарата показали, что барабан, перемещая растительную массу, имеет большую, чем ворох скорость.
117

Это приводит к тому, что ворох проскальзывает относительно барабана, и за время нахождения колосьев в зазоре по ним наносится несколько ударов бичей.
Если выбрать на барабане фиксированный радиус, проходящий через входную планку деки, то за время t он повернется на угол ψ. За это же время поступившая в подбарабанье порция растительной массы повернется на угол φ относительно оси барабана, при этом и .
Для определения скорости необходимо прежде всего установить взаимосвязь между скоростями растительной массы и барабана, а также определить функцию (t) , т.е. характер изменения скорости
порции во времени или по углу охвата.
Пусть углы поворота барабана ψ и хлебной массы θ будут использованы в качестве обобщенных координат системы барабан - хлебная масса.
С известным приближением можно полагать, что средние скорости барабана и порции вороха за время t могут быть выражены полусуммами величин скоростей на границах интервала, тогда
б t / 2 ;
1 t / 2 ,
где ωб – угловая скорость барабана на холостом ходу; ω1 – угловая скорость порции массы в подбарабанье;
, – текущие угловые скорости барабана и порции растений. Из этих уравнений следует, что
2 б t ; 2 t .
После определения времени t из каждого уравнения |
|
t 2 / б ; |
t 2 / 1 |
можно приравнять правые части формул и получить уравнение связи для θ и ψ:
2 |
|
2 |
; |
1 б ; |
1 6 , |
|
|
|
|||||
б |
1 |
|||||
|
|
|
|
|||
откуда 6 1 0. |
|
|||||
Одним из наиболее общих способов описания динамики системы механических элементов является составление уравнения Аппеля:
S |
Q , |
(5.32) |
|
|
|||
|
|
||
S |
|
|
где S – энергия ускорений;
S – независимая обобщенная координата;
Qμ – обобщенная сила, соответствующая независимой обобщенной координате.
Применительно к движению барабана и хлебной массы в молотильном зазоре энергия ускорений может быть представлена уравнением:
S 12 I 2 12 mR2 2 ,
118

где I – момент инерции барабана; m – масса порции вороха.
Частная производная энергии ускорений по независимой обобщен-
ной координате будет равна: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
S |
|
|
|
S |
|
|
I mR2 |
|
. |
|
(5.33) |
|||||
|
|
|
S |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ускорение на основании уравнения связи можно выразить через : |
|||||||||||||||||||
|
|
6 1 и |
|
|
|
б б |
, |
||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
откуда следует, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
(5.34) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Уравнение (5.33) с учетом соотношения (5.34) примет вид: |
|
||||||||||||||||||
|
|
|
S |
|
|
|
S |
I mR2 . |
(5.35) |
||||||||||
|
|
|
S |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обобщенная сила, соответствующая независимой обобщенной коор- |
|||||||||||||||||||
динате, равна: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
Q |
Fi |
Ai , |
|
|
|
(5.36) |
|||||||
i 1
где Fi - внешние активные силы, приложенные к элементам системы; Ai - вектор Аппеля –
Ai ri ,
S
где ri – путь, проходимый элементами системы.
К молотильному барабану приложен внешний активный крутящий момент, расходуемый на ускорение барабана Му и порций хлебной массы Мм, причем,
Му = FyR, MM = N f1 R,
где Fy – сила, затрачиваемая на ускорение барабана, отнесенная к его бичам.
Внешней силой, тормозящей движение вороха в молотильном зазоре, будет только N f2 – сила трения стеблей о деку, которая направлена в противоположную по отношению к скорости соломы сторону (рис. 5.33).
Рис. 5.33. Силы, действующие на порцию хлебной массы
в молотильном зазоре
119

С учетом этих значений уравнение для определения обобщенных сил можно записать в таком виде:
Q Fy Nf1 A1 Nf2 A2 .
Полагая разницу между величинами радиусов барабана и деки несу-
щественной, можно получить |
|
|
|
|
r1 = Rψ , r2 = Rθ , |
r |
R , |
r |
R . |
|
1 |
|
2 |
|
Принимая во внимание эти значения и соотношение по уравне-
нию (5.34), можно определить векторы Аппеля:
А1 r1 R R ;
А2 r2 R R ,
и тогда уравнение примет вид:
Q Fy N f1 R N f2 R .
Уравнение Аппеля для исследуемой системы запишется тогда в сле-
дующей форме: |
|
|
|
|
|
|
|
|
|
|
|
I mR2 |
|
Fy R N f1 R N f2 R |
|
. |
(5.37) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
Поскольку |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
то |
2 |
|
|
f |
|
|
|
|
I F R , |
mR NR f |
|
|
. |
|
||||||
|
y |
|
|
|
1 |
|
|
|
2 |
|
|
Полученное уравнение содержит сомножитель ψ/θ, учитывающий проскальзывание барабана относительно порции вороха. При отсутствии скольжения, т.е. когда ψ = θ, формула (5.37) превращается в обычное уравнение динамики, составленное на основе второго закона Ньютона.
Это уравнение можно преобразовать на основе соотношений (стр.
118):
|
|
|
|
|
f |
|
|
mR2 NR f |
|
б |
|
2 |
. |
||
|
1 |
1 |
|
|
|||
|
|
|
|
|
|||
При нормальном рабочем режиме барабана колебания его угловой скорости не превосходят 3…4%, влиянием которых на величину скорости порции стеблей в подбарабанье можно пренебречь. В этом случае
|
const и |
mR2 |
|
|
2 |
|
|
|
||||||
NR f |
|
|
f |
2 |
. |
|||||||||
|
|
|||||||||||||
б |
|
|
|
|
|
|
|
1 |
1 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Введя обозначения |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
N R f |
2 |
|
H , |
2 |
f |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
D |
|
|
|
|
|||
|
|
m R2 |
|
|
f |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
и заменяя переменную ω1 + θ = у, можно получить
120
