156

4.4. Решение систем линейных уравнений матричным способом (с

помощью обратной матрицы)

Рассмотрим линейную систему

b1 = b2

- столбец неизвестных, B - столбец свободных членов.

Kbn

Тогда исходную систему можно записать в виде матричного уравнения:

A × X = B .

32

Основная матрица A такой системы квадратная. Определитель этой

определитель системы отличен от нуля, то система называется

невырожденной.

Найдем решение данной системы уравнений в случае ∆ ≠ 0.

33

Отсюда на основании определения равенства матриц следует, что

x1 = 4 , x2 = 3 , x3 = 5.

5.Решение матричных уравнений

Рассмотрим решение матричных уравнений следующего вида:

1) AX = B и 2) YA = C ,

где A – заданная квадратная матрица порядка n , A ¹ 0 , B , C – заданные прямоугольные матрицы размеров n × r и r × n , соответственно, X , Y –

искомые матрицы размеров n × r и r × n , соответственно.

1. AX = B . Умножим слева обе части уравнения на матрицу A−1 :

A−1 × A × X = A−1 × B , или E × X = A−1 × B ,

или

E × X = A−1 × B , X = A−1 × B − искомое решение.

2. YA = C . Умножим слева обе части уравнения на матрицу A−1 :

Y × A × A−1 = C × A−1 ,

34

Решение.

6.Ранг матрицы

Рассмотрим матрицу A размера m × n

Выделим в этой матрице произвольные K строк и K столбцов.

Элементы, стоящие на пересечении выделенных строк и столбцов, образуют квадратную матрицу порядка K .

Минором K -го порядка матрицы A называется определитель квадратной матрицы, получившийся из данной матрицы выделением K

строк и K столбцов.

Пример 27. Рассмотреть миноры различных порядков матрицы

Решение.

Для матрицы, имеющей 3 строки и 4 столбца, одним из миноров 3-го

Сами элементы можно рассматривать как миноры 1-го порядка.

Рангом матрицы называется порядок ее наибольшего ненулевого

минора. Обозначается r , r( A) или rang( A) .

Решение.

36

Все миноры 3-го порядка равны нулю. Есть минор 2-го порядка,

Отметим свойства ранга матрицы:

1.При транспонировании матрицы ее ранг не меняется.

2.Если вычеркнуть из матрицы нулевой ряд, то ранг матрицы не изменится.

3.Ранг матрицы не изменяется при элементарных преобразованиях матрицы.

Матрицы, имеющие одинаковые ранги, называются эквивалентными.

Для матриц большой размерности непосредственное вычисление всех миноров затруднительно. Поэтому в этом случае можно преобразовать матрицу к ступенчатому виду, воспользовавшись операциями, не изменяющими ранг матрицы (эквивалентными преобразованиями).

Напомним, что к ним относятся:

1)транспонирование;

2)умножение строки на ненулевое число;

3)перестановка строк;

4)прибавление к элементам данной строки элементов любой другой строки, умноженных на ненулевое число;

5)вычеркивание нулевой строки.

Решение.

Следовательно, r( A) = 2 .

7.Исследование систем линейных уравнений

Базисным минором матрицы называется любой ее ненулевой минор,

порядок которого равен рангу матрицы.

комбинации λ1 = λ2 =K = λn = 0 .

Теорема 4. Строки и столбцы матрицы, элементы которых входят в

базисный минор, линейно независимы.

38

Теорема 5. Любая строка (столбец) матрицы является линейной комбинацией строк (столбцов) базисного минора.

Пусть дана произвольная система m линейных уравнений с n неизвестными

Теорема 6. (Кронекера – Капелли). Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы.

Неизвестные, коэффициенты при которых входят в базисный минор матрицы системы, называются базисными неизвестными, а остальные -

свободными неизвестными.

Из теоремы следует, что для системы m уравнений с n неизвестными возможны следующие случаи:

1. Найти ранги основной и расширенной матриц системы. Если r( A) ¹ r(A B), то система несовместна.

2. Если r( A) = r(B) = r , система совместна. При этом:

а) если r = n ( n – число неизвестных), то система имеет единственное решение;

б) если r < n , то система имеет бесконечное число решений.

В случае r < n , r переменных x1, x2 ,K, xr называются основными

(базисными), если определитель матрицы из коэффициентов при них (т. е.

базисный минор) отличен от нуля. Остальные n − r переменных называются

39

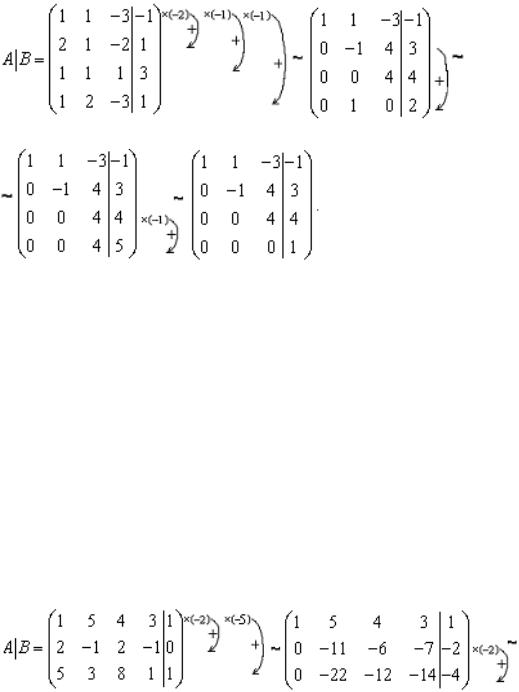
неосновными (или свободными).

x1 + x2 − 3x3 = −1

2x1 + x2 − 2x3 = 1

Пример 30. Исследовать на совместность систему x1 + x2 + x3 = 3 .

x1 + 2x2 − 3x3 = 1

Решение.

Приведем расширенную матрицу к ступенчатому виду

Очевидно, что r(A) = 3; r(B) = 4 . По теореме Кронекера-Капелли система не совместна.

Пример 31. Исследовать на совместность, и в случае совместности

х1 + 5х2 + 4х3 + 3х4 = 1

решить систему 2х1 − х2 + 2х3 − х4 = 0 .

5х1 + 3х2 + 8х3 + х4 = 1

Решение.

Приведем расширенную матрицу к ступенчатому виду:

40

Очевидно, r( A) = r( A B) = 2 , т.е. r < n , система имеет множество

х1 + 5х2 + 4х3 + 3х4 = 1

решений. Решаем систему двух уравнений − 11х2 − 6х3 − 7х4 = −2 .

Необходимо выбрать свободные и зависимые переменные. Пусть x1 , x2

– базисные неизвестные, а x3 , x4 – свободные неизвестные. Тогда выразим из системы уравнений х1 и х2 :

41