
книги / Цифровая обработка сигналов
..pdf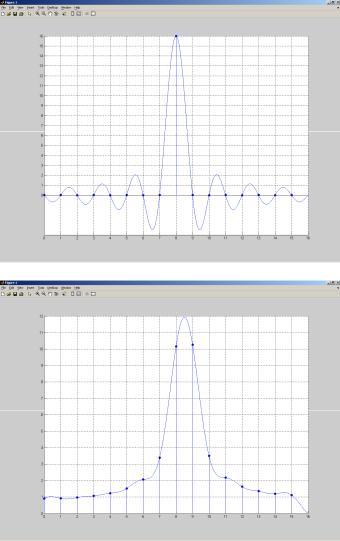
Рассмотрим непрерывный синусоидальный сигнал, дискретизированный с частотой fs = 32 кГц и подвергнутый 32-точечному дискретному преобразованию Фурье. На рис. 3.4 приведены варианты
Рис. 3.4. Спектры ДПФ для разных входных частот
41
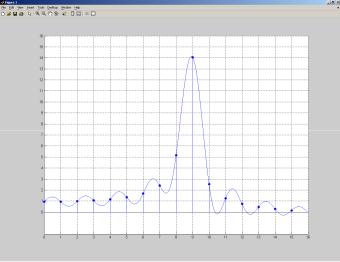
Рис. 3.4. Окончание
спектров для входной частоты 8 кГц (кратной аналитической частоте 32 000/32 = 1 000 Гц), а также входных частот 8,5 и 8,75 кГц. На рис. 3.4 наглядно проиллюстрировано явление утечки ДПФ.
Необходимо отметить, что при размножении спектра дискретизированного сигнала относительно частот ±kfs, где k – любое целое число, боковые лепестки спектра могут быть искажены боковыми лепестками соседних копий спектра. Для уменьшения этого явления применяется метод «взвешивание окном».
Взвешивание окном
Метод взвешивания окном применяется для уменьшения утечки ДПФ за счет понижения уровня боковых лепестков характеристики. Это позволяет значительно уменьшить искажения из-за наложения копий спектра дискретной последовательности. Взвешивание окном реализуется за счет умножения дискретной входной последовательности x(n) на отсчеты функции окна w(n):
N 1
X w (m) w(n)x(n)e j 2 nm/ N .
n 0
Приведем математические описания некоторых видов окна, которыенаиболеечастоприменяютсяприцифровойобработкесигналов:
42

Название окна |
Математическое описание |
||
Прямоугольное окно |
|
w(n) = 1, n = 1,2, …, N–1. |
|
Треугольное окно |
w(n) = n/(N/2), n = 1,2, …, N/2, |
||
|
w(n) = 2 |
– n/(N/2), n = N/2+1,2, …, N–1. |
|
Окно Хэннинга (Хана) |
w(n) = 0,5 |
– |
0,5cos(2πn/N – 1), n = 1,2, …, N–1. |
Окно Хэмминга |
w(n) = 0,54 |
– |
0,46cos(2πn/N – 1), n = 1,2, …, N–1. |
На рис. 3.5 приведена иллюстрация метода взвешивания входной синусоидальной функции разными видами окон.
а
e
b |
|
f |
c |
g |
|
d |
|
h |
Рис. 3.5. Иллюстрация взвешивания окном: a – входной сигнал, b – прямоугольное окно, c – входной сигнал, взвешенный прямоугольным окном, d – треугольное окно, e – входной сигнал, взвешенный треугольным окном, f – окно Хэннинга (Ханна), g – сигнал, взвешенный окном Хэннинга (Ханна), h – окно Хэмминга
43
Из-за малых значений на концах окон потери сигнала характе-
ризуются коэффициентом обработки (коэффициентом потерь ок-
на). Для того чтобы их точнее проанализировать, применяют логарифмический масштаб характеристики. На рис. 3.6 приведены характеристики модулей спектров разных окон в линейном и логарифмическом масштабах.
а
а
б
б
Рис. 3.6. Характеристики модулей спектров разных окон в линейном и логарифмическом масштабах; б – результаты взвешивания окном Хэмминга для сигналов 8,5 и 8,75 кГц
44

Из анализа характеристик, приведенных на рис. 3.6, очевидно, что по отношению к прямоугольному окну остальные виды окон имеют более широкий спектр основного лепестка, однако утечка по боковым лепесткам у них существенно ниже.
На рис. 3.7 показаны результаты взвешивания окном для сигналов с характеристиками, показанными на рис. 3.4.
Рис. 3.7. Результаты взвешивания окном Хэмминга для сигналов 8,5 и 8,75 кГц
Можно указать еще одно преимущество взвешивания окном – обнаружение слабого сигнала в присутствии близкого по частоте
45

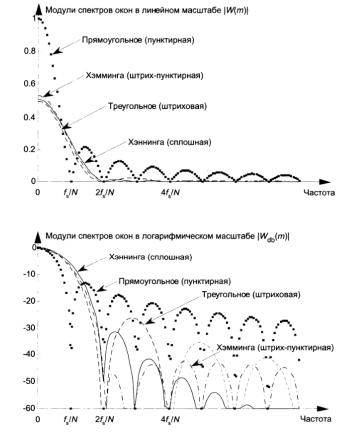
мощного сигнала. Из-за утечки ДПФ для более мощного компонента обнаружение более слабого компонента без взвешивания окном было бы весьма затруднительно. На рис. 3.8 показаны характеристики модулей ДПФ сложного гармонического сигнала, который состоит из синусоиды амплитуды 1,0 частоты между m = 3 и 4 и синусоиды амплитуды 0,1 частоты m = 7. Из рис. 3.8 видно, что без
а
б
Рис. 3.8. Обнаружение слабого компонента сложного сигнала на фоне утечки ДПФ при взвешивании окном:
а – графическая иллюстрация; б – результат моделирования
46
взвешивания окном из-за утечки ДПФ слабый компонент сигнала с m = 7 практически не выделяется, а взвешивание окном позволяет его обнаружить.
Для улучшения оценки спектра при помощи ДПФ используется метод «дополнение нулями». Он позволяет улучшить (увеличить) разрешающую способность ДПФ.
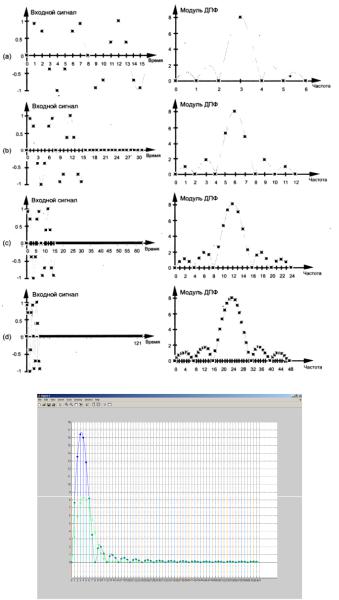
Дополнение нулями реализуется за счет увеличения количества отсчетов простым добавлением определенного количества нулей (L) после дискретизации входной последовательности (N), а затем расчета (N+L)-точечного ДПФ. Добавление увеличивает количество данных, а следовательно, и точность аппроксимации дискретным спектром ДПФ реального непрерывного спектра. На рис. 3.9 проиллюстрировано улучшение ДПФ за счет добавления нулей.
Существует определенный предел, при котором увеличение разрешающей способности (количества точек преобразования) не дает существенных результатов.
Необходимо отметить, что взвешивание окном необходимо производить перед дополнением нулями. Это так, поскольку в противном случае часть окна будет обнулена и искажена, что приведет к ошибочным результатам.
Можно сделать вывод, что увеличение точек преобразования и взвешивание окном являются основными направлениями улучшения ДПФ, и они должны комбинироваться для получения оптимального (с точки зрения точности и вычислительной сложности) результата.
В заключение рассмотрим иллюстрацию одного из применений ДПФ – определение спектра зашумленного сигнала (рис. 3.10). На входе системы передачи формируется сигнал x(t) = sin(2 50t) + 1,5sin(2 200t), который дискретизируется с частотой fs = 2000 Гц. Несмотря на наложение аддитивной помехи типа «белый шум», соизмеримой с параметрами сигнала, в результате вычисления преобразования Фурье можно определить явно выраженные частоты 50 и 200 Гц, а также амплитуды соответствующих гармоник – 1 и 1,5.
47
а
б
Рис. 3.9. Иллюстрация улучшения ДПФ за счет добавления нулей:
а – иллюстрация; б – результат моделирования в среде MathWorks MatLab
48

Существует
Рис. 3.10. Пример определения спектра зашумленного сигнала
3.3. Быстрое преобразование Фурье
Для уменьшения количества математических операций при вычислении дискретного преобразования Фурье был разработан алгоритм быстрого ДПФ (БПФ). Указанный алгоритм основан на определенной перегруппировке элементов ДПФ, т.е. это не аппроксимация (приближение), а в точности ДПФ. Все свойства ДПФ (линейность, симметрия, сдвиг, утечка) сохраняются и для БПФ.
Наибольшее применение получили алгоритмы БПФ, в которых количество точек N кратно степени числа 2 (их также называют БПФ по основанию 2). Это объясняется тем, что в таком случае можно выполнить каскадное (последовательное) вычисление, использовав простейшее 2-точечное ДПФ.
Обычное ДПФ требует реализации примерно N2 комплексных умножений при вычислении. Напротив, БПФ требует реализации примерно (N/2)log2N комплексных умножений, поэтому эффективность применения БПФ увеличивается с ростом N.
49
Алгоритм БПФ основан на минимизации количества математических операций вычисления за счет разбиения суммы ДПФ на две суммы с четными и нечетными индексами соответственно:
N 1 |
|
( N /2) 1 |
X (m) x(n)e j 2 nm/ N |
x(2n)e j 2 2nm/ N |
|
n 0 |
|
n 0 |
|
( N /2) 1 |
|
|
x(2n 1)e j 2 (2n 1)m/ N . |
|
n 0
Вынесем за сумму нечетных индексов множитель e–j2πm/N. Обозначим параметр e–j2π/N через WN (назовем его поворачивающий множитель), тогда:
e–j2πm/N = (WN)m, e–j2π2nm/N = (WN) 2nm, (WN)2 =
=e–j2π2/N = e–j2π/(N/2) = WN/2.
Сучетом выполненных обозначений получим:
|
( N /2) 1 |
( N /2) 1 |
X (m) |
x(2n)(WN /2 )nm (WN )m |
x(2n 1)(WN /2 )nm . |
|
n 0 |
n 0 |
Из приведенного выражения видно, что количество математических операций уже уменьшилось за счет однократного вычисления коэффициентов W. Дополнительный выигрыш получается за счет разбиения последовательности ДПФ длиной N на две части (пополам). РассмотримопределениекомпонентаДПФ синдексом(m + N/2):
|
|
|
|
|
( N /2) 1 |
|
|
|
|
|
|
X (m N / 2) |
x(2n)(WN /2 )n(m N /2) |
|
|
||||
|
|
|
|
|
n 0 |
|
|
|
|
|
|
|
|
( N /2) 1 |
|
|
|
|
|
|
|
(WN )(m N /2) |
x(2n 1)(WN /2 )n(m N /2) . |
|
|
||||
|
|
|
|
n 0 |
|
|
|
|
|
Преобразуем коэффициенты W: |
|
|
|
|
|||||
(W |
)n(m N /2) |
(W |
)nm (W |
N /2 |
)nN /2 (W |
N /2 |
)nm e j 2 n2N /(2N ) (W |
N /2 |
)nm , |
N /2 |
|
N /2 |
|
|
|
|
|||
(WN )(m N /2) (WN )m (WN )N /2 (WN )m e j 2 nN /(2 N ) (WN )m ( 1) (WN )m .
50
