
книги / Цифровая обработка сигналов
..pdf
ваются математической формулой, которая точно или приближенно характеризует соответствующий физический процесс. Для определения параметров сигнала указанного описания вполне достаточно. Для дискретных сигналов и систем описание реализуется в виде последовательности чисел, по которым, не зная дополнительной информации, невозможно определить параметры сигнала. Самым важным дополнительным параметром является интервал (шаг, период) дискретизации. Действительно, имея только дискретные значения сигнала и не имея информации об их расположении друг относительно друга, о форме и параметрах сигнала можно только догадываться. Поэтому выбор значения периода дискретизации и наличие об этом информации в дискретной системе являются принципиальным моментом для цифровой обработки сигналов.
Рис. 1.2. При подаче на вход сигнала дискретная система выдает выходной сигнал: а – входной и выходной сигналы представляют собой последовательности отдельных значений; б – входной и выходной сигналы обозначаются как х(п) и у(п)
Как известно из теории связи, сигнал имеет представление не только во временной, но и в частотной области. Это представление дает возможность анализировать частотные свойства сигнала, которые необходимы для выбора параметров канала связи, а также соответствующих алгоритмов преобразования и анализа сигналов. Временное и частотное представления связаны друг с другом через преобразование Фурье, котороепозволяет осуществлятьпереход между ними [2].
Рассмотрим иллюстрацию соответствия временного и частотного представлений сигнала на примере негармонического непрерывного сигнала вида xsum (t) sin 2 f0t 0,4sin 2 2 f0t и соответствующего
11
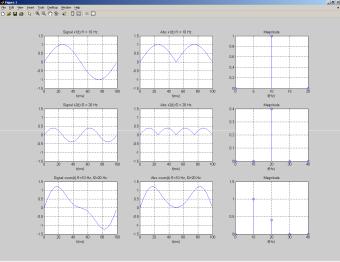
ему дискретного сигнала xsum (n) sin 2 f0nts 0,4sin 2 2 f0nts (см. Приложение). Сигнал содержит две гармоники с частотами f0 и 2f0
(рис. 1.3).
а |
б |
в |
Рис. 1.3. Графические представления во временной и частотной областях: а – синусоидальный сигнал частотой f0, синусоидальный сигнал пониженной амплитуды с частотой 2f0, сумма двух сигналов; б– мощностисигналов; в– спектрысигналов
В цифровой обработке сигналов используют и временное, и частотное представления, а также преобразования между ними.
Введем понятия мгновенного значения и амплитуды сигналов, которые часто считают эквивалентными, но это не так. Мгновенное значение сигнала показывает, как и в каком направлении относительно нуля он изменяется. Поэтому мгновенное значение может принимать и отрицательное, и положительное значения. Амплитудой принято называть модуль наибольшего отклонения сигнала относительно нуля, т.е. амплитуда всегда положительна. На рис. 1.4 показан график изменения модуля гармонического сигнала x1 (n) sin 2 f0nts .
12

Рис. 1.4. График изменения модуля сигнала x1 (n) sin 2f0 nts
Часто при анализе сигналов интересуются не только уровнем сигнала, но и его мощностью. Мощность пропорциональна квадрату амплитуды сигнала. Если взять коэффициент пропорциональности, равный 1, как это часто делают на практике, то
P (n) x(n)2 |
|
|
x(n) |
|
2 , P (m) X (m)2 |
|
|
X (m) |
|
2 , |
|
|
|
|
|||||||
t |
|
|
|
|
|
|
|
|
|
|
где Pt(n) – мощность сигнала во временной области; Pω(n) – мощность сигнала в частотной области, взятая с интервалом m. На рис. 1.5 изображены графики модулей и мощности сигнала xsum (t) sin 2 f0t 0,4sin 2 2 f0t в частотной области.
Рис. 1.5. Графики модулей и мощности сигнала xsum(t)
Можно указать, что все операции при цифровой обработке сигналов осуществляются над последовательностями чисел. Сами по себе операции являются простейшими арифметическими или их комбинациями и могут быть достаточно просто реализованы в соответствующем аппаратно-программном базисе. Условные обозначения операций в дискретных системах показаны на рис. 1.6.
13

Рис. 1.6. Термины и условные обозначения, применяемые в блок-схемах описания цифровой обработки сигналов
Введем понятие линейной дискретной системы. Назовем дис-
кретную систему линейной, если выполняются следующие условия: 1. Если сигнал x1(n) вызывает реакцию y1(n), сигнал x2(n)
вызывает реакцию y2(n), то сигнал x1(n) + x2(n) вызывает реакцию
y1(n) + y2(n).
2. Если сигнал c1·x1(n) вызывает реакцию c1·y1(n), сигнал
c2·x2(n) вызывает реакцию c2·y2(n), то сигнал c1·x1(n) + c2·x2(n) вызывает реакцию c1·y1(n) + c2·y2(n). Указанное условие называют еще
свойством пропорциональности (гомогенности или однородности).
14
Системы, для которых одно из указанных выше условий не выполняется, называются нелинейными.
Рассмотрим характеристики линейной и нелинейной дискретных систем, на вход которых подаются одни и те же входные воздействия – два синусоидальных сигнала с разными параметрами, а также сумма указанных двух сигналов.
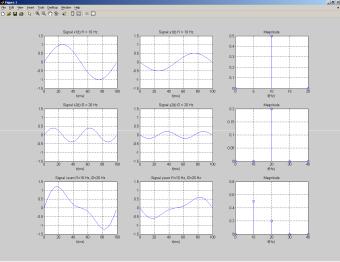
На рис. 1.7 приведены характеристики линейной дискретной системы, описываемой уравнением y = – x/2, а на рис. 1.8 – нелинейной дискретной системы, описываемой уравнением y = x2 [3]. В первом и втором рядах показаны характеристики подачи единичного синусоидального сигнала (входной сигнал, выходной сигнал, спектр выходного сигнала), а в третьем – аналогичные характеристики суммарного сигнала. По рис. 1.7 и 1.8 можно сделать вывод, что для линейной системы спектр суммарного выходного сигнала совпадает с суммой спектров его составляющих и может быть вычислен по ним, а для нелинейной системы такой вывод сделать нельзя.
Рис. 1.7. Иллюстрация спектральных свойств линейных дискретных систем
15
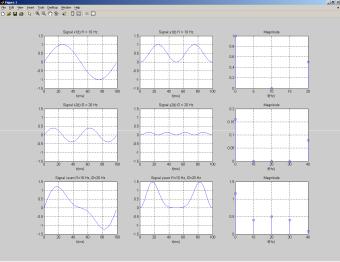
Рис. 1.8. Иллюстрация спектральных свойств нелинейных дискретных систем
Введем понятие инвариантной во времени дискретной сис-
темы. Для этого сформулируем условие инвариантности: задержка (сдвиг) во времени во входном дискретном сигнале приводит к эквивалентному (т.е. такому же) сдвигу и в выходном дискретном сигнале. Для непрерывных систем сформулированное условие относилось бы к равенству сдвигов фаз. Математически приведенное условие выглядит так:
x(n + k) → y(n + k),
где k – целое число, указывающее количество интервалов дискретизации, на которое происходит сдвиг.
Иногда в литературе термин инвариантности во времени отождествляют с термином стационарности. Это неправильно, поскольку под стационарностью понимается свойство системы иметь характеристики, не зависящие от времени, а это совсем не относится к устойчивости относительно временного сдвига.
Можно утверждать, что любые линейные инвариантные системы (ЛИВ) обладают свойством коммутативности, что проиллюстрировано на рис. 1.9.
16
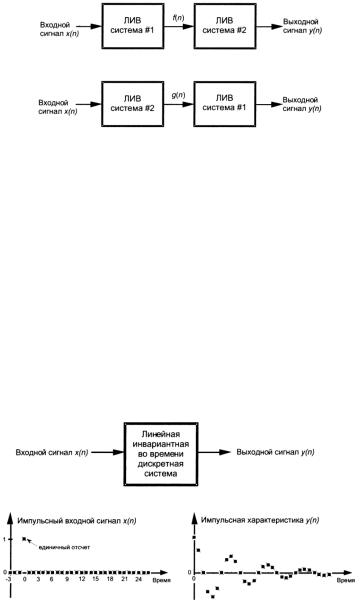
Рис. 1.9. Иллюстрация свойства коммутативности линейных инвариантных систем
Очевидно, что промежуточные последовательности f(n) и g(n) при разных расположениях систем будут отличаться, однако это обычно не имеет значения.
Рассмотрим способы описания линейных систем. Линейные системы, как правило, описываются дифференциальными уравнениями. При помощи преобразования Лапласа можно перейти из временной в комплексную плоскость относительно переменной p, затем построить передаточную функцию системы в виде H(jω) = Y(jω)/X(jω). Однако для анализа линейных инвариантных систем достаточно иметь информацию только лишь об импульсной характеристике – реакции системы на входное воздействие в виде функции Дирака (δ-функции) (рис. 1.10).
а
б
Рис. 1.10. Описание системы: а – блок-схема системы; б – импульсная характеристика
17
Контрольные вопросы и задания
1.Почему первые системы передачи назывались аналоговыми?
2.Чем отличаются дискретные и цифровые сигналы?
3.Виды дискретизации.
4.Какие процессы выполняются при преобразовании сигнала из непрерывного в цифровой?
5.Что понимается под «отсутствием сигнала (например, импульса)?
6.С помощью какого преобразования осуществляется переход между временным и частотным представлениями сигналов?
7.Какие типовые математические операции выполняются при цифровой обработке сигналов?
8.Проверить, удовлетворяют ли условиям линейности указан-
ные системы: y(n) = –x1(n)/2, y(n) = [x1(n)]2, y(n) = Y0(1 + + x1(n))sin(ω0t). Взять в качестве x(t) гармонический сигнал. Постро-
ить представление сигналов во временной и частотной областях. 9. Рассмотреть справедливость утверждений:
– любая линейная система инвариантна во времени;
– любая инвариантная во времени система линейна;
– любая инвариантная во времени система стационарна;
– любая стационарная система инвариантна во времени.
10. Рассмотреть проверку на инвариантность во времени следующих систем: y(n) = –x1(n)/2, y(n) = [x1(n)]2, y(n) = Y0(1 + + x1(n))sin(ω0t).
18
2.ПЕРИОДИЧЕСКАЯ ДИСКРЕТИЗАЦИЯ
2.1.Общие принципы. Наложение (aliasing)
Периодическая дискретизация – это процедура преобразования непрерывных сигналов в последовательность дискретных отсчетов, которая применяется в любой области цифровой обработки сигналов. Основная задача заключается в выборе значения частоты (или периода) дискретизации, которая позволит на приеме достаточно точно воспроизвести и обработать принятую последовательность. Поэтому рассмотрим вопросы, связанные с реализацией процедуры дискретизации для сигналов, расположенных в различных частях частотного спектра [1].
На практике могут применяться два основных способа дискретизации: адаптивная (с переменным шагом дискретизации) и неадаптивная (с постоянным шагом дискретизации). Неадаптивная дискретизация нашла наибольшее применение из-за более простой реализации и достаточной точности восстановления, поэтому далее будем говорить только о ней.
Выбор частоты дискретизации fs (или периода дискретизации ts) осуществляется из теоремы В.А. Котельникова:
f |
|
|
1 |
2F |
, если f |
|
; |
|
|
|
||
s |
0, F |
|
|
|||||||||
|
|
|
||||||||||
|
|
ts |
max |
|
|
|
max |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
1 |
2(F |
|
F |
), если f |
|
|
|
. |
|
s |
|
F |
, F |
|||||||||
|
|
|||||||||||
|
|
ts |
max |
min |
|
|
|
min |
max |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
Можно утверждать, что чем сложнее сигнал (чем шире его спектр), тем с большей частотой его нужно дискретизировать, т.е. взять большее количество отсчетов для его более точного восстановления. Рассмотрим связанную с этим условием неоднозначность, получившую название «наложение» (aliasing).
Рассмотрим возникновение явления наложения на примере дискретизации гармонического сигнала x(t) sin 2 f0t . При дискретиза-
ции его с частотой fs получаем дискретный сигнал x(n) sin 2 f0nts .
19
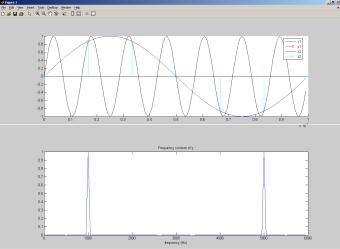
Гармонические функции периодичны, т.е. повторяются через 2π радиан. Следовательно, можно представитьдискретный сигнал так:
x(n) sin(2 f0nts 2 m),
где m – любое целое число. Далее
x(n) sin 2 ( f |
|
|
m |
)nt |
s |
sin 2 ( f |
|
m f |
s |
)nt |
s |
|
0 |
|
0 |
||||||||||
|
|
nts |
|
n |
|
|
||||||
sin 2 ( f0 kfs )nts sin 2 f0nts .
Аргументы у гармонической функции совпадают, следовательно, получаем: f0 = f0 + kfs. Это означает, что дискретизация сигнала с частотой f0 даст последовательность, совпадающую с последовательностью, полученной при дискретизации сигнала с частотой f0 + kfs. При этом частота дискретизации fs одна и та же. Спектр любой дискретной последовательности содержит периодически повторяющиеся копии исходного спектра непрерывного сигнала.
Пример 2.1.
1. Возьмем гармонический сигнал f0 = 7 кГц и выполним его дискретизацию с частотой fs = 6 кГц. Согласно полученным выше
Рис. 2.1. Иллюстрация дискретизации разных сигналов одной частотой дискретизации
20
